Numerical modeling (geology)

Simulation of seismic wave propagation in global scale using supercomputer to solve wave equations

In Geology, numerical modeling is a widely applied technique to tackle complex geological problems by simulation of geological scenarios quantitatively.

Numerical modeling is based on mathematical models that describe the physical conditions of geological scenarios using numbers and equations. Nevertheless, some equations used are difficult to solve directly, such as partial differential equations. Numerical model uses numerical methods, such as finite difference method, to approximate the solutions of these equations. Numerical experiments can then be performed in these models and the results are interpreted. Qualitative understanding of various processes involved may also be obtained from these experiments.

History

Prior to the development of numerical modeling, analog modeling, which simulates nature with reduced scale in mass, length and time, was one of the major ways to tackle geological problems. For instance, the formation of thrust belts. Simple analytic or semi-analytic mathematical models were also used to deal with relatively simple geological problems quantitatively.

In the late 1960s to 1970s, following the development of finite-element methods in solving problems of continuum mechanics in civil engineering, numerical methods were adapted in modeling complex geological phenomena, for example folding and mantle convection. With advances in computer technology, the accuracy of numerical models has been improved. Numerical modeling has become an important tool for tackling geological problems, especially for the parts of the Earth that are difficult to observe directly, such as the mantle and core. Yet analog modeling is still useful in modeling geological scenario that are difficult to be captured in numerical models, and the combination of analog and numerical modeling will be useful to improve our understanding of the Earth's processes.

Components

Steps in numerical modeling. The first step in numerical modeling is to capture the actual geological scenario quantitatively. For example, in mantle convection modeling, heat equations are used to describe the heat energy circulating in the system while Naiver-Stokes equations describe the flow of viscous fluid (the mantle rock). Second, since these equations are difficult to solve, discretization and numerical methods are chosen to make approximation to the governing equations. Then, algorithms in the computer can calculate the approximated solutions. Finally, interpretation can be made from those solutions. For instance, in mantle convection modeling, the flow of mantle can first be visualized. Then, the relationship between the patterns of flow and the input parameters maybe concluded.

A general numerical model usually consists of the following components:

1. Mathematical model is a simplified description of the geological problem, such as equations and boundary conditions. These governing equations of the model are often partial differential equations that are difficult to solve directly since it involves the derivative of the function, for example, the wave equation.
2. Discretization methods and numerical methods convert those governing equations in the mathematical models to discrete equations. These discrete equation can approximate the solution of the governing equations. Common methods include finite element, finite difference, finite volume method that subdivide the object of interest into smaller pieces (element) by mesh. These discrete equations can then be solved in each element numerically. Discrete element method uses another approach, this method reassemble the object of interest from numerous tiny particles. Simple governing equation are then applied to the interactions between particles.
3. Algorithms are computer programs that compute the solution using the idea of the above numerical methods.
4. Interpretation are made from the solutions given by the numerical models.

Properties

A good numerical model usually has some of the following properties:

• Consistent. Numerical models often divide the object into smaller element. If the model is consistent, the result of numerical model is nearly the same as what the mathematical model predicts when the element size is nearly zero. In other words, the error between the discrete equations used in the numerical model and the governing equations in the mathematical model tends to zero when the space of the mesh (size of element) close to zero.
• Stable. In a stable numerical model, the error during the computation of the numerical methods do not amplify. The error of an unstable model will stack up quickly and leads to incorrect result. A stable and consistent numerical model have the same output as the exact solution in the mathematical model when the space of mesh (size of element) is extremely small.
• Converging. The output of the numerical model is closer to the actual solution of the governing equations in the mathematical models when the spacing of mesh (size of element) reduces, which is usually checked by carrying out numerical experiments.
• Conserved. The physical quantities in the models, such as mass and momentum, are conserved. Since the equations in the mathematical models are usually derived from various laws of conservation, the model result should violate these premises.
• Bounded. The solution given by the numerical model is in reasonable physical bounds with respect to the mathematical models, for instance mass and volume should be positive.
• Accurate. The solution given by the numerical models is close to the real solution predicted by the mathematical model.

Computation

The following are some key aspects of ideas in developing numerical models in geology. First, the way to describe the object should be decided (kinematic description). Then, governing equations that describe the geological problems are written, for example, the heat equations describe the flow of heat in a system. Since some of these equations cannot be solved directly, numerical methods are used to approximate the solution of the governing equations.

Kinematic descriptions

Main article: Lagrangian and Eulerian specification of the flow field

In numerical model and mathematical model, there are two different approaches to describe the motion of matter: Eulerian and Lagrangian. In geology, both approaches are commonly used to model fluid flow like mantle convection, where an Eulerian grid is used for computation and Lagrangian markers are used to visualize the motion. Recently, there are models tried to describe different parts using different approaches to combine the advantages of these two approach, this combined approach is called arbitrary Lagrangian-Eulerian approach.

Eulerian

Eulerian approach considers the changes of the physical quantities, such as mass and velocity, of a fixed location with time. It is similar to look at how the river water flow on a bridge. Mathematically, the physical quantities can be expressed as a function of location and time. It is useful for fluid and homogeneous (uniform) materials that have no natural boundary.

Lagrangian

Lagrangian approach, on the other hand, considers the change of physical quantities, such as the volume, of fixed elements of matter with time. It is similar to look at a particular boat floating on a river. Lagrangian approach is useful for solid.

Kinematic descriptions

• 
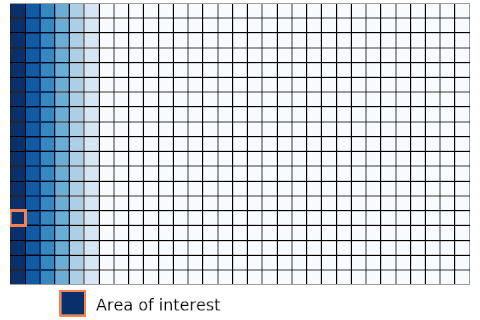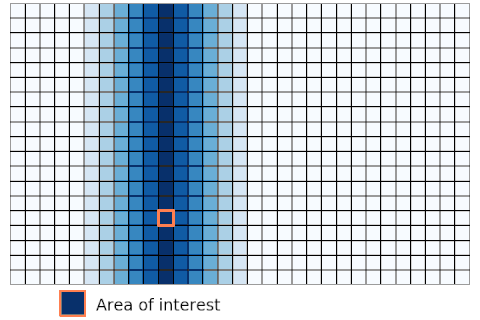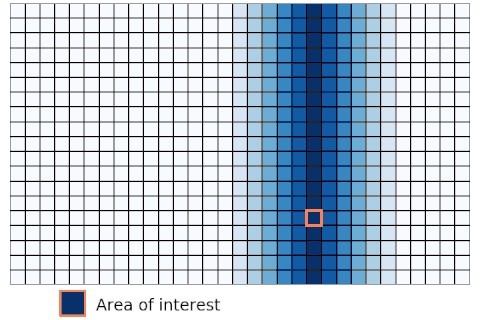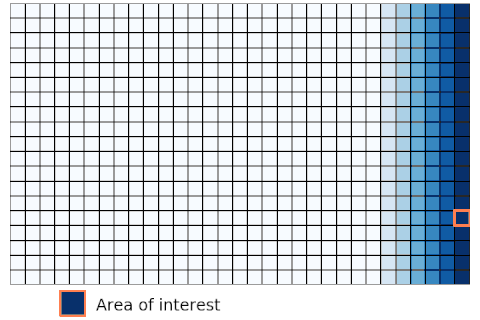
  Eulerian approach In the figure, the orange box indicates the area of interest. In eulerian approach, the location of the red box is fixed, while the change of color of that box is considered
• 
  Lagrangian approach. In the figure, the orange box indicates the area of interest. In lagrangian approach, the location of the red box is not fixed, it moves over time. The area of interest is always the same element.

Governing equations

Main article: Governing equation

The following equations are some basic equations that are commonly used in describing physical phenomena, for example, how the matter in a geologic system moves or flows and how heat energy distributed in a system. These equations are usually the core of the mathematical model.

Continuity equation

Main article: Continuity equation

Continuity equation is a mathematical version of stating the geologic object or medium is continuous, which means no empty space can be found in the object. This equation is commonly used in numerical modeling in geology.

For instance, the continuity equation of mass of fluid. Based on the law of conservation of mass, for a fluid with density $\rho$ at position $x_{j}$ in a fixed volume $V$ of fluid, the rate of change of mass is equals to the outward fluid flow across the boundary $S$:

${\frac {\partial }{\partial t}}\int \limits _{V}\rho d\tau =-\int \limits _{S}\rho u_{j}dS_{j}$

where $\tau$ is the volume element and $u_{j}$ is the velocity at $x_{j}$.

In Lagrangian form:

${\frac {D\rho }{Dt}}\equiv {\frac {\partial \rho }{\partial t}}+u_{j}{\frac {\partial \rho }{\partial x_{j}}}=-\rho {\frac {\partial u_{j}}{\partial x_{j}}}$

In Eulerian form:

${\frac {\partial \rho }{\partial t}}={\frac {\partial (\rho u_{j})}{\partial x_{j}}}$

This equation is useful when the model involves the continuous fluid flow, like the mantle is in geological time scale.

Momentum equation

Main articles: Equations of motion and Navier–Stokes equations

The momentum equation describes how matter moves in response to force applied, it is an expression of Newton's second laws of motion.

Consider a fixed volume $V$ of matter, by the law of conservation of momentum, the rate of change of volume is equal to:

• external force $F$ applied on the element
• plus normal stress and shear stress applied on the surface $S$ bounding the element
• minus the momentum moving out of the element on that surface

${\frac {\partial }{\partial t}}\int \limits _{V}\rho u_{i}d\tau =\int \limits _{V}\rho F_{i}d\tau +\int \limits _{S}\sigma _{ij}dS_{j}-\int \limits _{S}\rho u_{i}u_{j}dS_{j}$

where $\tau$ is the volume element, $u$ is the velocity.

After simplifications and integrations, for any volume $V$, the eulerian form of this equation is:

$\rho {\frac {\partial u_{i}}{\partial t}}+\rho u_{j}{\frac {\partial u_{i}}{\partial x_{j}}}=\rho F_{i}+{\frac {\partial \sigma _{ij}}{\partial x_{j}}}$

Heat equation

Main articles: Heat equation and Convection–diffusion equation

The heat equations describe how heat energy flow in a system.

From the law of conservation of energy, the rate of change of energy $E$ of a fixed volume $V$ of mass is equal to:

• work done at the boundary $S$
• plus work done by external force $F$ in the volume $V$
• minus heat conduction across boundary $S$
• minus heat convection across boundary $S$
• plus heat produced internally

Mathematically:

${\frac {\partial }{\partial t}}\int \limits _{V}\rho Ed\tau =\int \limits _{S}u_{i}\sigma _{ij}dS_{j}+\int \limits _{V}\rho u_{i}F_{i}d\tau -\int \limits _{S}k{\frac {\partial T}{\partial x_{j}}}dS_{j}-\int \limits _{S}\rho Eu_{j}dS_{j}+\int \limits _{V}\rho Hd\tau$

where $\tau$ is the volume element, $u$ is the velocity, $T$ is the temperature, $k$ is the conduction coefficient and $H$ is the rate of heat production.

Numerical methods

An example of 2D finite element mesh. The domain is subdivided into numerous non-overlapping triangles (elements). Nodes are the vertices of the triangles.

Numerical methods are techniques to approximate the governing equations in the mathematical models.

Common numerical methods include finite element method, spectral method, finite difference method, finite volume method. These methods are used to approximate the solution of governing differential equations in the mathematical model by disseminating the domain into meshes or grids and applying simpler equations to individual elements or nodes in the mesh.

Approximating wave equations using finite element method. The domain is subdivided into numerous triangles. The values of the nodes in the mesh are calculated, showing how a wave propagate in the region.

Discrete element method uses another approaches, the object is considered an assemblage of small particles.

Finite element method

Main article: Finite element method

The finite element method subdivide the object (or domain) into smaller, non-overlapping elements (or subdomains) and these elements are connected at the nodes, the solution for the partial differential equations are then approximated by simpler element equations, usually polynomials. Then these element equations are combined into equations of the entire object, i.e. the contribution of each element is summed up to model the response of the whole object. It is commonly used to solve mechanical problems. The following are the general steps of using finite element method:

1. Select the element type and subdivide the object. Common element types include triangular, quadrilateral, tetrahedral, etc. Different types of elements should be chosen for different problems. See also: types of mesh
2. Decide the function of displacement. The function of displacement governs how the elements move. Linear, quadratic, cubic polynomial functions are commonly used.
3. Decide the displacement-strain relation. The displacement of the element changes (deform) the elements' shape (strain). This relation calculates how much strain the element experienced due to the displacement.
4. Decide the strain-stress relation. The deformation of the element induces stress to the element, which is the force applied to the element. This relation calculates the amount of stress experienced by the elements due to the strain. One of the examples of this relation is Hooke's Law
5. Derive equations of stiffness and stiffness matrix for elements. The stress also causes the element to deform, the stiffness (the rigidity) of the elements indicates how much it will deform in response the stress. The stiffness of the elements in different directions are represented in matrix form for simpler operation during calculation
6. Combine the element equations into global equations. The contributions of every element are summed up to a set of equations that describe the whole system.
7. Apply boundary conditions. The predefined conditions at the boundary, such as temperature, stress and other physical quantities are introduced to the boundary of the system.
8. Solve for displacement. As time evolves, the displacement of the elements are solved step by step.
9. Solve for strains and stress. After the displacement is calculated, the strains and stress are computed using the relations in 3 and 4.

Solution of Burgers Equation, which describes how shock waves behave, using spectral method. The domain is first subdivided into rectangular mesh. The idea of this method is similar to finite element method.

Spectral method

Main article: Spectral method

Spectral method is similar to finite element method. The major difference is that spectral method uses basis functions, such as using Fast Fourier Transformation (FFT) that approximate the function by the sum of numerous basis functions. These kinds of basis function can then be applied to the whole domain and approximate the governing partial differential equations. Therefore, each calculation takes the information from the whole domain into account while finite element method only take the information from the neighborhood. As a result, spectral method converges at exponential manner and it is suitable for solving problems involving a high variability in time or space.

Finite volume method

Main article: Finite volume method

Finite volume method is also similar to finite element method, it also subdivides the object of interest into smaller volume (or element), then the physical quantities are solved over the control volume as fluxes of these quantities across the different faces. The equations used are usually based on the conservation or balance of physical quantities, like mass and energy.

Finite volume method can be applied on irregular mesh like the finite element method and the element equations are still intuitive physically like the finite difference method, however, it is difficult to get a better accuracy as the higher order version of element equations are not well-defined.

Finite difference method

Main articles: Finite difference method and Finite difference

Finite difference method approximate differential equations by approximating the derivative with difference equation which is the major method to solve partial differential equations.

Finite difference method

Consider a function $f(x)$ with single-valued derivatives that are continuous and finite functions of $x$, according to Taylor's theorem:

$f(x+\Delta x)=f(x)+\Delta xf'(x)+{\frac {1}{2}}\Delta x^{2}f''(x)+{\frac {1}{6}}\Delta x^{3}f'''(x)+\cdots$

and

$f(x-\Delta x)=f(x)-\Delta xf'(x)+{\frac {1}{2}}\Delta x^{2}f''(x)-{\frac {1}{6}}\Delta x^{3}f'''(x)+\cdots$

Summing up the above expressions:

$f(x+\Delta x)+f(x-\Delta x)=2f(x)+\Delta x^{2}f''(x)+{\text{terms with higher than 4th power of }}\Delta x$

Ignore the terms with higher than 4th power of $x$, then:

$f''(x)\simeq {\frac {1}{\Delta x^{2}}}\left[f(x+\Delta x)-2f(x)-f(x-\Delta x)\right]$

$f'(x)\simeq {\frac {1}{2\Delta x}}\left[f(x+\Delta x)-f(x-\Delta x)\right]$

The above is the central-difference approximation of the derivatives, which can also be approximated by forward-difference:

$f'(x)\simeq {\frac {1}{\Delta x}}\left[f(x+\Delta x)-f(x)\right]$

or backward-difference:

$f'(x)\simeq {\frac {1}{\Delta x}}\left[f(x)-f(x-\Delta x)\right]$

The accuracy of the finite differences can be improved when more the higher order terms are used.

Discrete element method

An example of model using discrete element method, which uses photo of Peter A. Cundall to initiate the particles

Main article: Discrete element method

Discrete element method, sometimes called distinct element method, is usually used to model discontinuous materials, such as rocks which has fractures like joints and bedding, since it can explicitly model the properties of discontinuities. The discrete element method was initially developed for modeling rock mechanics problems.

The main idea of this method is to model the objects as an assemblage of smaller particles, which is similar to building a castle out of sand. These particles are of simple geometry, such as sphere. The physical quantities of each particle, such as velocity, are continuously updated at the contacts between them. This model is relatively computational intensive as a large quantity of particles needed to be used, especially for large scale models, like a slope. Therefore, this model are usually applied to small scale objects.

Bonded-particle model

There are objects that are not composed of granular materials, such as crystalline rocks are composed of mineral grains that are stick with each other or interlocked with each other. Some bonding between particles are added to model this cohesion or cementation between particles, this kind of model are also called bonded-particle model.

Applications

Numerical modeling can be used to model problems in different fields of geology at various scales, such as engineering geology, geophysics, geomechanics, geodynamics, rock mechanics and hydrogeology. The following are some examples of applications of numerical modeling in geology.

Specimen to outcrop scale

Rock Mechanics

Numerical modeling has been widely applied in different fields of rock mechanics. Rock is a material that is difficult to model because rock are usually:

• Discontinuous: there are numerous fractures and micro-fractures in a rock mass and the space in the rock mass maybe filled with other substances like air and water. Complex model is needed to fully capture these discontinuities since the discontinuities have great effects to the rock mass.
• Anisotropic: the properties of rock mass, such as permeability (the ability to allow fluid to flow through), may varies at different directions.
• Inhomogeneous: the properties of different portions of the rock mass maybe different. For example, the physical properties of quartz grains and feldspar grains are different in granite.
• Not elastic: Rock cannot perfectly revert to its original shape after stress is removed.

In order to model the behaviors of rock, a complex model that take all the above characteristics are needed. There are many models modeling rock as continuum using method like finite difference, finite element and boundary element methods. One of the disadvantages is that the ability of modeling cracks and other discontinuities are usually limited in these model. Models that modeling rock as discontinuum using method like discrete element and discrete fracture network methods, are also commonly used. The combinations of both methods are also developed.

Numerical modeling enhanced the understanding in the mechanical processes in the rock by conducting numerical experiment and it is useful for design and construction works.

Regional-scale

Thermochronology

Numerical modeling has been used to predict and describe thermal history of the Earth crust, which allows geologists to improve their interpretation of thermochronological data. Thermochronology can tell the temperature of rock experienced at particular time. The geologic events, like the development of fault, can change the thermochronological pattern on the surface and it is possible to constrain the geologic events by these data. Numerical modeling can be used to predict the pattern.

The difficulties of in the thermal modeling of the Earth's crust are mainly the irregularity and the changes of the Earth's surface (mainly erosion) through time, therefore in order to model the morphological changes of the Earth surface, the models need to solve heat equations with a boundary conditions change with time and irregular meshes.

Pecube

Pecube is one of the numerical model developed to predict the thermalchronological pattern. It solved the following generalized heat transfer equation with advection using finite element method. The first three terms on the right-hand side is the heat transferred by conduction in $x$, $y$ and $z$ directions while $A$ is the advection. $${\frac {\partial T}{\partial t}}+u{\frac {\partial T}{\partial x}}+v{\frac {\partial T}{\partial y}}+w{\frac {\partial T}{\partial z}}={\frac {\partial }{\partial x}}\kappa {\frac {\partial T}{\partial x}}+{\frac {\partial }{\partial y}}\kappa {\frac {\partial T}{\partial y}}+{\frac {\partial }{\partial z}}\kappa {\frac {\partial T}{\partial z}}+A$$ After the temperature field is constructed in the model, particle paths are traced and the cooling history of the particles can be obtained. The pattern of thermochronological age can then be computed.

A cross-section showing the thermal and exhumation patterns of the crust generated by the movement of a fault. The simulation is generated by Pecube [Helsinki University Geodynamics Group (HUGG) version]. The model is three-dimensional, the figure shows a slice of the model for simplicity. In the figure, the white line indicates the fault. The small black arrows indicate the direction of movement of the material at that point. The red lines are isotherm (the point of the line are of same temperature) The Pecube model uses both eulerian and lagrangian approach. The fault can be regarded as stationary and the crust is moving. Initially, the temperature of crust depends on the depth. The deeper the depth, the hotter the material is. During this event, the motion of crust along the fault moves the material with different temperature. In the hanging wall (the block above the fault), hotter material in deeper depth moves towards the surface; while the cooler material at shallower depth in the footwall (the block below the fault) moves to a deeper depth. The flow of material changes the thermal pattern (the isotherm bends across the fault) of the crust, which may reset the thermochronometers in the rock. On the other hand, the exhumation rate also affects the thermochronometers in the rock. A positive rate of exhumation indicates the rock is moving towards the surface, while a negative rate of exhumation indicate the rock is moving downwards. The fault geometry has impacts the pattern exhumation rate on the surface.

Hydrogeology

See also: Hydrogeology § Numerical method, Groundwater model, and MODFLOW

In hydrogeology, groundwater flow is often modeled numerically by finite element method and finite difference method. These two methods have been shown to produce similar results if the mesh is fine enough.

Finite difference grid used in MODFLOW

MODFLOW

One of the well-known program in modeling groundwater flow is the MODFLOW developed by the United States Geological Survey, it is a free and open-source program that uses finite difference method as the framework to model groundwater conditions. The recent development of related program developed offers more features including:

• Interactions between groundwater and surface-water systems
• Transportation of solute
• Flow of fluid with variable density, such as salt water
• Compaction of aquifer system
• Subsidence of land
• Management of groundwater

Crustal dynamics

The rheology (response of materials to stress) of crust and the lithosphere is complex since a free surface (the land surface), the plasticity and elasticity of the crustal materials are needed to be considered. Most of the models uses finite element methods with Lagrangian mesh. One of the example usage include the study of deformation and kinematics of subduction.

FLAC

The Fast Lagrangian Analysis of Continua (FLAC) is one of the most popular approaches in modeling crustal dynamics. The approach is fast as it solves the equations of momentum and continuity without using matrix, hence it is fast but time steps must be small enough. The approach has been used in both 2D, 2.5D and 3D studies of crustal dynamics, in which the 2.5D results were generated by combining multiple slices of 2D results.

This figure shows the setup of the numerical model used in the study of tectonic evolution of the Cathaysia Block, which makes up the southeast part of South China carton. This model uses the code called Flamar, which is a FLAC-like code that combined finite difference and finite element method. The element used in this Lagrangian mesh is quadrilateral. The boundary conditions applied to the land surface is free, which is affected by erosion and sediment deposition. The boundary on the sides is at constant velocity, which will push the crust to subduct. The boundary condition used at the bottom is called Winkler's pliable basement, it is at hydrostatic equilibrium and it allows the base to slip freely horizontally.

Global-scale

Mantle convection

A simulation of mantle convection in a form of a quarter of 2D annulus using ASPECT. In the model, the temperature of the core-mantle boundary (inner boundary) is a constant of 4273 K (about 4000℃), while that at the boundary between crust and mantle (outer boundary) is 973 K (about 700℃). The mesh in the simulation changes over time. The code uses adaptive mesh refinement, the mesh is finer in the areas that need more accurate calculation, such as the rising plumes, while the mesh is coarser in other area to save the computational power. In the figure, red color indicates a warmer temperature while blue color indicate a cooler temperature, hot material rises from the core mantle boundary due to lower density. When the hot material reaches the outer boundary, it starts to move in horizontally and eventually sinks due to cooling.

There are many attempts to model mantle convection.

Finite element, finite volume, finite difference and spectral methods have all been used in modeling mantle convection, and almost every models used an Eulerian grid. Due to the simplicity and speed of finite-difference and spectral method, they were used in some early models, but finite-element, finite volume methods are usually adopted now. Many benchmark papers have investigated the validity of these numerical models. Current approaches mostly uses a fixed and uniform grid. Grid refinement, in which the size of the elements is reduced in the part that require more accurate approximation, is possibly the direction of future development in numerical modeling of mantle convection.

Finite difference approach

In the 1960s to 1970s, mantle convection models using finite difference approach usually use second-order finite differences. Stream function are used to remove the effect of pressure and reduce the complexity of the algorithm. Due to the advancement in computer technology, finite differences with higher order terms are now used to generate a more accurate result.

Finite volume approach

Convection of the mantle that modeled by finite volume approach often based on the balance between pressure and momentum, the equations derived is the same as the finite difference approach using a grid with staggered velocity and pressure, in which the values of velocity and the pressure of each element are located at different locations. These approach can maintain the coupling between velocity and pressure can be maintained.

Multiple codes are developed based on this finite difference/finite volume approach. In modeling 3 dimensional geometry of the Earth, since the parameters of mantles vary at different scales, multigrid, which is using different grid sizes for different variables, are used to overcome the difficulties. Example includes cubed sphere grid, ‘Yin-Yang’ grid and spiral grid.

Finite element approach

In finite element approach, stream functions are also often used in reducing the complexity of the equations. ConMan, modeling 2 dimensional incompressible flow in the mantle, was one of the popular code for modeling mantle convection in the 1990s. CitCom, an eulerian mutlgrid finite element model, is one of the most popular program to model mantle convection in 2D and 3D now.

Spectral method

Spectral method in mantle convection breaks down the 3 dimensional governing equation into several 1 dimensional equations, which solve the equations much faster and it was one of the popular approach in early models of mantle convection. Many program are developed using this method during the 1980s to early 2000s. However, the lateral changes of viscosity of mantle is difficult to manage in this approach, so that other methods are more popular now.

The Earth is believed to be consisted several plates. Numerical model can be used to model the kinematics of plates.

Plate tectonics

Plate tectonics is a theory suggesting that the Earth's lithosphere are essentially plates floating on the mantle. The mantle convection model is fundamental in modeling the plates floating on it, and there are two major approaches to incorporate the plates into the mantle convection model: rigid-block approach and rheological approach. The rigid-block approach assumes the plates are rigid, which means the plates keep its shape and do not deform, just like some wooden blocks floating on water; while the rheological approach model the plate as a highly viscous fluid that the equations applied to the lithosphere beneath them also applies to the plates.

Geodynamo

Numerical models have been made to verify the geodynamo theory, a theory that suggested that the geomagnetic field was generated by the motion of conductive fluid in the Earth's core.

Modeling of the flow of Earth's liquid outer core is difficult because:

• the Coriolis effect due to the Earth's rotation cannot be ignored
• the magnetic field generated will also generate Lorentz force, which will affect the motion of the conductive fluid in the liquid outer core
• the low viscosity of liquid iron, which makes the fluid flow hard to model

Most of the models uses spectral method to simulate the geodynamo, for example the Glatzmaier-Roberts model. Finite difference method has also been used in the model by Kageyama and Sato. Some study also tried other methods, like finite volume and finite element methods.

A numerical geodynamo model (Glatzmaier-Roberts model) showing the magnetic field generated by the flowing liquid outer core. This figure shows how the magnetic field of the Earth behave during magnetic reversal.

Seismology

Simulation of seismic wave propagation through the Earth.

Finite difference methods has been widely used in simulation of propagation of seismic waves. However, due to the limitation in computation power, in some models, the space of the mesh are too large (comparing with the wavelength of the seismic waves) that the results are inaccurate due to grid dispersion, the seismic waves with different frequencies separated. Some researchers suggest to use spectral method to model seismic wave propagation.

Errors and limitations

Sources of error

Despite numerical modeling providing accurate quantitative estimation to geological problems, there is always difference between the actual observation and the modeling results because of:

• the simplification of the actual problem in building the numerical model. Since there are numerous factors that can affect a geological system, it is nearly impossible to take everything into account. Therefore, a numerical model usually simplifies the actual system by omitting the less significant factors. For instance, the Earth is often modeled as a sphere despite the undulation of Earth's surface.
• the approximations or idealizations of the governing equations. Many objects in the nature are complex, it is impossible to capture all the characteristics using equations. For instance, rocks are discontinuous but modeling rock as a continuous material is reasonable at large scale as it describes the properties accurate enough.
• the approximations in discretization process. Since the governing equations in the model cannot be solved directly, approximations to these equations are made using discretization and numerical methods.
• the uncertainty in physical parameters. For example, the models of the viscosity of mantle and core are not accurate.

Limitations

Apart from the errors, there some limitations in using numerical models.

• Users of the models need high level of knowledge and experience to prevent misuse and misinterpretations of the numerical model.

See also

• Geologic modeling
• Numerical analysis

Wikibooks has a book on the topic of: Introduction to Numerical Methods