Circumcircle

Circumscribed circle, C, and circumcentre, O, of a cyclic polygon, P

In geometry, the circumscribed circle or circumcircle of a polygon is a circle which passes through all the vertices of the polygon. The centre of this circle is called the circumcenter.

A polygon which has a circumscribed circle is called a cyclic polygon. All regular simple polygons, all triangles and all rectangles are cyclic.

A related notion is the one of a minimum bounding circle, which is the smallest circle that completely contains the polygon within it. Not every polygon has a circumscribed circle, as the vertices of a polygon do not need to all lie on a circle. Yet any polygon has a unique minimum bounding circle, which may be constructed by a linear time algorithm.^[1] Even if a polygon has a circumscribed circle, it may not coincide with its minimum bounding circle; for example, for an obtuse triangle, the minimum bounding circle has the hypotenuse as diameter and does not pass through the opposite vertex.

Circumcircles of triangles

Construction of the circumcircle (red) and the circumcentre (red dot)

All triangles are cyclic, i.e. every triangle has a circumscribed circle.

The circumcenter of a triangle can be found as the intersection of the three perpendicular bisectors. (A perpendicular bisector is a line that forms a right angle with one of the triangle's sides and intersects that side at its midpoint.) This is because the circumcenter is equidistant from any pair of the triangle's points, and all points on the perpendicular bisectors are equidistant from those points of the triangle.

In coastal navigation, a triangle's circumcircle is sometimes used as a way of obtaining a position line using a sextant when no compass is available. The horizontal angle between two landmarks defines the circumcircle upon which the observer lies.

The circumcentre's position depends on the type of triangle:

• If and only if a triangle is acute (all angles smaller than a right angle), the circumcenter lies inside the triangle
• If and only if it is obtuse (has one angle bigger than a right angle), the circumcenter lies outside
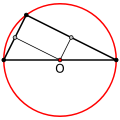
• If and only if it is a right triangle, the circumcenter lies on one of its sides (namely, the hypotenuse). This is one form of Thales' theorem.

• 
  The circumcentre of an acute triangle is inside the triangle
• 
  The circumcentre of a right triangle is on the hypotenuse
• 
  The circumcentre of an obtuse triangle is outside the triangle

The diameter of the circumcircle can be computed as the length of any side of the triangle, divided by the sine of the opposite angle. (As a consequence of the law of sines, it doesn't matter which side is taken: the result will be the same.) The triangle's nine-point circle has half the diameter of the circumcircle.

In any given triangle, the circumcenter is always collinear with the centroid and orthocenter. The line that passes through all of them is known as the Euler line.

The isogonal conjugate of the circumcenter is the orthocenter.

The useful minimum bounding circle of three points is defined either by the circumcircle (where three points are on the minimum bounding circle) or by the two points of the longest side of the triangle (where the two points define a diameter of the circle.). It is common to confuse the minimum bounding circle with the circumcircle.

The circumcircle of three collinear points is an infinitely large circle. Nearly collinear points often cause problems and errors in computation of the circumcircle.

Circumcircles of triangles have an intimate relationship with the Delaunay triangulation of a set of points.

Circumcircle equations

The circumcircle is given in Cartesian coordinates by the equation

$\det {\begin{vmatrix}v^{2}&v_{x}&v_{y}&1\\A^{2}&A_{x}&A_{y}&1\\B^{2}&B_{x}&B_{y}&1\\C^{2}&C_{x}&C_{y}&1\end{vmatrix}}=0$

where A, B and C are the vertices of the triangle, and the solution for v is the circumcircle. (Note A² = A_x² + A_y².)

Given

$a=\det {\begin{vmatrix}A_{x}&A_{y}&1\\B_{x}&B_{y}&1\\C_{x}&C_{y}&1\end{vmatrix}},\quad S_{x}={\frac {1}{2}}\det {\begin{vmatrix}A^{2}&A_{y}&1\\B^{2}&B_{y}&1\\C^{2}&C_{y}&1\end{vmatrix}},\quad S_{y}={\frac {1}{2}}\det {\begin{vmatrix}A_{x}&A^{2}&1\\B_{x}&B^{2}&1\\C_{x}&C^{2}&1\end{vmatrix}},$

$b=\det {\begin{vmatrix}A_{x}&A_{y}&A^{2}\\B_{x}&B_{y}&B^{2}\\C_{x}&C_{y}&C^{2}\end{vmatrix}}$

we then have av² − 2Sv − b = 0 and, assuming the three points were not in a line (otherwise the circumcircle is that line that can also be seen as a generalized circle with S at infinity), (v − S/a)^{2 = b/a + S2/a2, giving the circumcenter S/a and the circumradius √ (b/a + S2/a2). This approach should also work for the circumsphere of a tetrahedron.}

An equation for the circumcircle in trilinear coordinates x : y : z is a/x + b/y + c/z = 0. An equation for the circumcircle in barycentric coordinates x : y : z is 1/x + 1/y + 1/z = 0.

The isogonal conjugate of the circumcircle is the line at infinity, given in trilinear coordinates by ax + by + cz = 0 and in barycentric coordinates by x + y + z = 0.

Coordinates of circumcenter

The circumcenter has trilinear coordinates (cos $\alpha$, cos $\beta$, cos $\gamma$) where $\alpha ,\beta ,\gamma$ are the angles of the triangle. The circumcenter has barycentric coordinates

$\left(a^{2}(-a^{2}+b^{2}+c^{2}),\;b^{2}(a^{2}-b^{2}+c^{2}),\;c^{2}(a^{2}+b^{2}-c^{2})\right),$

where $a,b,c$ are edge lengths ($BC,CA,AB$ respectively) of the triangle.

The angles at which the circle meets the sides

File:Circumcircle.angles.png

The angles at which the circumscribed circle meet the sides of the triangle coincide with angles at which sides meet each other. The side opposite angle α meets the circle twice: once at each end; in each case at angle α (similarly for the other two angles). The alternate segment theorem states that the angle between the tangent and chord equals the angle in the alternate segment.

Triangle centers on the circumcircle of triangle ABC

In this section, the vertex angles are labeled A, B, C and all coordinates are trilinear coordinates:

• Steiner point = bc/ (b² − c²) : ca/ (c² − a²) : ab/(a² − b²) = the nonvertex point of intersection of the circumcircle with the Steiner ellipse. (The Steiner ellipse, with center = centroid(ABC), is the ellipse of least area that passes through A, B, and C. An equation for this ellipse is 1/(ax) + 1/(by) + 1/(cz) = 0.)

• Tarry point = sec (A + ω) : sec (B + ω) : sec (C + ω) = antipode of the Steiner point

• Focus of the Kiepert parabola = csc (B − C) : csc (C − A) : csc (A − B)

Cyclic quadrilaterals

Cyclic quadrilaterals

Main article: Cyclic quadrilateral

Quadrilaterals that can be circumscribed have particular properties including the fact that opposite angles are supplementary angles (adding up to 180° or π radians).

See also

• inscribed circle
• Jung's theorem, an inequality relating the diameter of a point set to the radius of its minimum bounding circle
• Lester's theorem

References

• ^ Megiddo, N. (1983). "Linear-time algorithms for linear programming in R³ and related problems". SIAM Journal on Computing. 12: 759–776.

• Kimberling, Clark (1998). "Triangle centers and central triangles". Congressus Numerantium. 129: i–xxv, 1–295.

External links

• Triangle centers by Antonio Gutierrez from Geometry Step by Step from the Land of the Incas.
• Triangle circumcircle and circumcenter With interactive animation
• Circumcircle at MathWorld
• Steiner circumellipse at MathWorld
• An interactive Java applet for the circumcenter