Spherical harmonics

In mathematics, the spherical harmonics are the angular portion of a set of solutions to Laplace's equation on the sphere. Represented in a system of spherical coordinates, Laplace's spherical harmonics $Y_{\ell }^{m}$ are a specific set of spherical harmonics which forms an orthogonal system, first introduced by Pierre Simon de Laplace. Spherical harmonics are important in many theoretical and practical applications, particularly in the computation of atomic electron configurations, representation of gravitational fields, geoids, and the magnetic fields of planetary bodies, and characterization of the cosmic microwave background radiation. In 3D computer graphics, spherical harmonics plays a special role in a wide variety of topics including indirect lighting (ambient occlusion, global illumination, precomputed radiance transfer, etc.) and in recognition of 3D shapes.

Introduction

Real (Laplace) spherical harmonics $Y_{\ell m}$, for $\ell =0$ to 4 (top to bottom) and $m=0$ to 4 (left to right). The negative order harmonics $Y_{\ell ,-m}$ are rotated about the $z$ axis by $90^{\circ }/m$ with respect to the positive order ones.

Laplace's equation in spherical coordinates is:

$\nabla ^{2}f={1 \over r^{2}}{\partial \over \partial r}\left(r^{2}{\partial f \over \partial r}\right)+{1 \over r^{2}\sin \theta }{\partial \over \partial \theta }\left(\sin \theta {\partial f \over \partial \theta }\right)+{1 \over r^{2}\sin ^{2}\theta }{\partial ^{2}f \over \partial \varphi ^{2}}=0$

(see also del in cylindrical and spherical coordinates). Consider the problem of finding solutions of the form ƒ(r,θ,φ) = r^ℓΘ(θ)Φ(φ), where ℓ is a non-negative integer. For ƒ of this special form, Laplace's equation reduces to

${\Phi (\varphi ) \over \sin \theta }{d \over d\theta }\left(\sin \theta {d\Theta \over d\theta }\right)+{\Theta (\theta ) \over \sin ^{2}\theta }{d^{2}\Phi \over d\varphi ^{2}}+\ell (\ell +1)\Theta (\theta )\Phi (\varphi )=0.$

Using the technique of separation of variables, two differential equations result:

${\frac {1}{\Phi (\varphi )}}{\frac {d^{2}\Phi (\varphi )}{d\varphi ^{2}}}=-m^{2}$

$\ell (\ell +1)\sin ^{2}(\theta )+{\frac {\sin(\theta )}{\Theta (\theta )}}{\frac {d}{d\theta }}\left[\sin(\theta ){\frac {d\Theta }{d\theta }}\right]=m^{2}$

for some m. Because Φ must be a periodic function whose period evenly divides 2π, m is necessarily an integer. Hence, the angular solutions can be shown to be a product of trigonometric functions and associated Legendre functions:

$Y_{\ell }^{m}(\theta ,\varphi )=N\,e^{im\varphi }\,P_{\ell }^{m}(\cos {\theta }),$

which fulfill

$\nabla ^{2}Y_{\ell }^{m}(\theta ,\varphi )=-\ell (\ell +1)Y_{\ell }^{m}(\theta ,\varphi ),$

on the unit sphere r = 1. Here $Y_{\ell }^{m}$ is called a spherical harmonic function of degree ℓ and order m, $P_{\ell }^{m}$ is an associated Legendre function, N is a normalization constant, and θ and φ represent colatitude and longitude, respectively. In particular, the colatitude θ, or polar angle, ranges from 0 at the North Pole to π at the South Pole, assuming the value of π/2 at the Equator, and the longitude φ, or azimuth, may assume all values with 0 ≤ θ ≤ 2π.

When Laplace's equation is solved on the surface of the sphere, the periodic boundary conditions in φ, as well as regularity conditions at both the north and south poles, ensure that the degree ℓ and order m are integers that satisfy ℓ ≥ 0 and |m| ≤ ℓ. In contrast, if the function ƒ were only to have been defined for θ ≤ θ₀, then the resulting spherical cap harmonics would have been defined for integer order, but non-integer degree. The general solution to Laplace's equation in a ball centered at the origin is a linear combination of the spherical harmonic functions multiplied by the appropriate scale factor r^ℓ,

$f(r,\theta ,\varphi )=\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }f_{\ell }^{m}\,r^{\ell }\,Y_{\ell }^{m}(\theta ,\varphi ),$

where the $f_{\ell }^{m}$ are constants and the factors $r^{\ell }\,Y_{\ell }^{m}$ are known as solid harmonics. Such an expansion is valid in the ball

$r<R=1/\limsup _{\ell \to \infty }|f_{\ell }^{m}|^{1/\ell }.$

Orthogonality and normalization

Several different normalizations are in common use for the spherical harmonic functions. In physics and seismology, these functions are generally defined as

$Y_{\ell }^{m}(\theta ,\varphi )={\sqrt {{(2\ell +1) \over 4\pi }{(\ell -m)! \over (\ell +m)!}}}\,P_{\ell }^{m}(\cos {\theta })\,e^{im\varphi }$

which are orthonormal

$\int _{\theta =0}^{\pi }\int _{\varphi =0}^{2\pi }Y_{\ell }^{m}\,Y_{\ell '}^{m'*}\,d\Omega =\delta _{\ell \ell '}\,\delta _{mm'},$

where δ_aa = 1, δ_ab = 0 if a ≠ b, (see Kronecker delta) and dΩ = sinθ dφ dθ. The disciplines of geodesy and spectral analysis use

$Y_{\ell }^{m}(\theta ,\varphi )={\sqrt {{(2\ell +1)}{(\ell -m)! \over (\ell +m)!}}}\,P_{\ell }^{m}(\cos {\theta })\,e^{im\varphi }$

which possess unit power

${1 \over 4\pi }\int _{\theta =0}^{\pi }\int _{\varphi =0}^{2\pi }Y_{\ell }^{m}\,Y_{\ell '}^{m'*}d\Omega =\delta _{\ell \ell '}\,\delta _{mm'}.$

The magnetics community, in contrast, uses Schmidt semi-normalized harmonics

$Y_{\ell }^{m}(\theta ,\varphi )={\sqrt {(\ell -m)! \over (\ell +m)!}}\,P_{\ell }^{m}(\cos {\theta })\,e^{im\varphi }$

which have the normalization

$\int _{\theta =0}^{\pi }\int _{\varphi =0}^{2\pi }Y_{\ell }^{m}\,Y_{\ell '}^{m'*}d\Omega ={4\pi \over (2\ell +1)}\delta _{\ell \ell '}\,\delta _{mm'}.$

In quantum mechanics this normalization is often used, too, and is there named Racah's normalization after Giulio Racah.

Using the identity (see associated Legendre functions)

$P_{\ell }^{-m}=(-1)^{m}{\frac {(\ell -m)!}{(\ell +m)!}}P_{\ell }^{m}$

it can be shown that all of the above normalized spherical harmonic functions satisfy

$Y_{\ell }^{m*}(\theta ,\varphi )=(-1)^{m}Y_{\ell }^{-m}(\theta ,\varphi ),$

where the superscript * denotes complex conjugation. Alternatively, this equation follows from the relation of the spherical harmonic functions with the Wigner D-matrix. The parity of the spherical harmonics is given by $(-1)^{\ell }$.

Condon-Shortley phase

One source of confusion with the definition of the spherical harmonic functions concerns a phase factor of (-1)^m, commonly referred to as the Condon-Shortley phase in the quantum mechanical literature. In the quantum mechanics community, it is common practice to either include this phase factor in the definition of the associated Legendre functions, or to append it to the definition of the spherical harmonic functions. There is no requirement to use the Condon-Shortley phase in the definition of the spherical harmonic functions, but including it can simplify some quantum mechanical operations, especially the application of raising and lowering operators. The geodesy and magnetics communities never include the Condon-Shortley phase factor in their definitions of the spherical harmonic functions.

Spherical harmonics expansion

The Laplace spherical harmonics form a complete set of orthonormal functions and thus form a vector space analogous to unit basis vectors. On the unit sphere, any square-integrable function can thus be expanded as a linear combination of these:

$f(\theta ,\varphi )=\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }f_{\ell }^{m}\,Y_{\ell }^{m}(\theta ,\varphi ).$

This expansion is exact as long as ℓ goes to infinity. Truncation errors will arise when limiting the sum over ℓ to a finite bandwidth $L$. The expansion coefficients can be obtained by multiplying the above equation by the complex conjugate of a spherical harmonic, integrating over the solid angle $\Omega \!\,$, and utilizing the above orthogonality relationships. For the case of orthonormalized harmonics, this gives:

$f_{\ell }^{m}=\int _{\Omega }f(\theta ,\varphi )\,Y_{\ell }^{m*}(\theta ,\varphi )d\Omega =\int _{0}^{2\pi }d\varphi \int _{0}^{\pi }d\theta \sin \theta f(\theta ,\varphi )Y_{\ell }^{m*}(\theta ,\varphi ).$

An alternative set of spherical harmonics for real functions may be obtained by taking the set:

$Y_{\ell m}={\begin{cases}Y_{\ell }^{0}&{\mbox{if }}m=0\\{1 \over {\sqrt {2}}}\left(Y_{\ell }^{m}+(-1)^{m}\,Y_{\ell }^{-m}\right)={\sqrt {2}}N_{(\ell ,m)}P_{\ell }^{m}(\cos \theta )\cos m\varphi &{\mbox{if }}m>0\\{1 \over i{\sqrt {2}}}\left(Y_{\ell }^{-m}-(-1)^{m}\,Y_{\ell }^{m}\right)={\sqrt {2}}N_{(\ell ,m)}P_{\ell }^{-m}(\cos \theta )\sin m\varphi &{\mbox{if }}m<0.\end{cases}}$

where $N_{(\ell ,m)}$ denotes the normalization constant as a function of ℓ and $m$. These functions have the same normalization properties as the complex ones above. In this notation, a real square-integrable function can be expressed as an infinite sum of real spherical harmonics as:

$f(\theta ,\varphi )=\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }f_{\ell m}\,Y_{\ell m}(\theta ,\varphi ).$

See here for a list of real spherical harmonics up to and including $\ell =5$. Note, however, that the listed functions differ by the phase (-1)^m from the phase given in this article.

Spectrum analysis

The total power of a function $f$ is defined in the signal processing literature as the integral of the function squared, divided by the area it spans. Using the orthonormality properties of the real unit-power spherical harmonic functions, it is straightforward to verify that the total power of a function defined on the unit sphere is related to its spectral coefficients by a generalization of Parseval's theorem:

${\frac {1}{4\,\pi }}\int _{\Omega }f(\Omega )^{2}\,d\Omega =\sum _{\ell =0}^{\infty }S_{f\!f}(\ell ),$

where

$S_{f\!f}(\ell )=\sum _{m=-\ell }^{\ell }f_{\ell m}^{2}$

is defined as the angular power spectrum. In a similar manner, one can define the cross-power of two functions as

${\frac {1}{4\,\pi }}\int _{\Omega }f(\Omega )\,g(\Omega )\,d\Omega =\sum _{\ell =0}^{\infty }S_{fg}(\ell ),$

where

$S_{fg}(\ell )=\sum _{m=-\ell }^{l}f_{\ell m}g_{\ell m}$

is defined as the cross-power spectrum. If the functions $f$ and $g$ have a zero mean (i.e., the spectral coefficients $f_{00}$ and $g_{00}$ are zero), then $S_{ff}(\ell )$ and $S_{fg}(\ell )$ represent the contributions to the function's variance and covariance for degree ℓ, respectively. It is common that the (cross-)power spectrum is well approximated by a power law of the form

$S_{f\!f}(\ell )=C\,\ell ^{\beta }.$

When $\beta =0$, the spectrum is "white" as each degree possesses equal power. When $\beta <0$, the spectrum is termed "red" as there is more power at the low degrees with long wavelengths than higher degrees. Finally, when $\beta >0$, the spectrum is termed "blue".

Addition theorem

A mathematical result of considerable interest and use is called the addition theorem for spherical harmonics. Two vectors r and r', with spherical coordinates $(r,\theta ,\varphi )$ and $(r',\theta ',\varphi ')$,respectively, have an angle $\,\!\gamma$ between them given by

$\cos \gamma =\cos \theta \cos \theta '+\sin \theta \sin \theta '\cos(\varphi -\varphi ').$

The addition theorem expresses a Legendre polynomial of order ℓ in the angle $\gamma$ in terms of products of two spherical harmonics with angular coordinates $(\theta ,\varphi )$ and $(\theta ',\varphi ')$:

$P_{\ell }(\cos \gamma )={\frac {4\pi }{2\ell +1}}\sum _{m=-\ell }^{\ell }Y_{\ell m}^{*}(\theta ',\varphi ')\,Y_{\ell m}(\theta ,\varphi ).$

This expression is valid for both real and complex harmonics. However, it should be emphasized that the quoted form above is valid only for the orthonormalized spherical harmonics. For unit power harmonics it is only necessary to remove the factor of $4\pi$.

Visualization of the spherical harmonics

Schematic representation of $Y_{\ell m}$ on the unit sphere and its nodal lines. $Y_{\ell m}$ is equal to 0 along $m$ great circles passing through the poles, and along $\ell -m$ circles of equal latitude. The function changes sign each time it crosses one of these lines.

3D color plot of the spherical harmonics of degree $n=5$

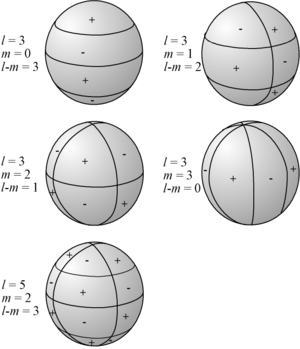
The Laplace spherical harmonics $Y_{\ell }^{m}$ can be visualized by considering their "nodal lines", that is, the set of points on the sphere where $Y_{\ell }^{m}$ vanishes. Nodal lines of $Y_{\ell }^{m}$ are comprised of circles: some are latitudes and others are longitudes. One can determine the number of nodal lines of each type by counting the number of zeros of $Y_{\ell }^{m}$ in the latitudinal and longitudinal directions independently. For the latitudinal direction, the associated Legendre functions possess ℓ−|m| zeros, whereas for the longitudinal direction, the trigonometric sin and cos functions possess 2|m| zeros.

When the spherical harmonic order m is zero, the spherical harmonic functions do not depend upon longitude, and are referred to as zonal. Such spherical harmonics are a special case of zonal spherical functions. When ℓ = |m|, there are no zero crossings in latitude, and the functions are referred to as sectoral. For the other cases, the functions checker the sphere, and they are referred to as tesseral.

More general spherical harmonics of degree ℓ are not necessarily those of the Laplace basis $Y_{\ell }^{m}$, and their nodal sets can be of a fairly general kind.

First few spherical harmonics

Analytic expressions for the first few orthonormalized Laplace spherical harmonics that use the Condon-Shortley phase convention:

$Y_{0}^{0}(\theta ,\varphi )={1 \over 2}{\sqrt {1 \over \pi }}$

$Y_{1}^{-1}(\theta ,\varphi )={1 \over 2}{\sqrt {3 \over 2\pi }}\,\sin \theta \,e^{-i\varphi }$

$Y_{1}^{0}(\theta ,\varphi )={1 \over 2}{\sqrt {3 \over \pi }}\,\cos \theta$

$Y_{1}^{1}(\theta ,\varphi )={-1 \over 2}{\sqrt {3 \over 2\pi }}\,\sin \theta \,e^{i\varphi }$

$Y_{2}^{-2}(\theta ,\varphi )={1 \over 4}{\sqrt {15 \over 2\pi }}\,\sin ^{2}\theta \,e^{-2i\varphi }$

$Y_{2}^{-1}(\theta ,\varphi )={1 \over 2}{\sqrt {15 \over 2\pi }}\,\sin \theta \,\cos \theta \,e^{-i\varphi }$

$Y_{2}^{0}(\theta ,\varphi )={1 \over 4}{\sqrt {5 \over \pi }}\,(3\cos ^{2}\theta -1)$

$Y_{2}^{1}(\theta ,\varphi )={-1 \over 2}{\sqrt {15 \over 2\pi }}\,\sin \theta \,\cos \theta \,e^{i\varphi }$

$Y_{2}^{2}(\theta ,\varphi )={1 \over 4}{\sqrt {15 \over 2\pi }}\,\sin ^{2}\theta \,e^{2i\varphi }$

$Y_{3}^{0}(\theta ,\varphi )={1 \over 4}{\sqrt {7 \over \pi }}\,(5\cos ^{3}\theta -3\cos \theta )$

More spherical harmonics up to Y₁₀

Higher dimensions

The classical spherical harmonics are defined as functions on the unit sphere S² inside three-dimensional Euclidean space. Spherical harmonics can be generalized to higher dimensional Euclidean space Rⁿ as follows. Let P_ℓ denote the space of homogeneous polynomials of degree ℓ in n variables. That is, a polynomial P is in P_ℓ provided that

$P(\lambda \mathbf {x} )=\lambda ^{\ell }P(\mathbf {x} ).$

Let A_ℓ denote the subspace of P_ℓ consisting of all harmonic polynomials; these are the solid spherical harmonics. Let H_ℓ denote the space of functions on the unit

$S^{n-1}=\{\mathbf {x} \in \mathbb {R} ^{n}\,\mid \,|x|=1\}$

obtained by restriction from A_ℓ.

The following properties hold:

• The spaces H_ℓ are dense in the set of continuous functions on Sⁿ⁻¹ with respect to the uniform topology, by the Stone-Weierstrass theorem. As a result, they are also dense in the space L²(Sⁿ⁻¹) of square-integrable functions on the sphere.

• For all ƒ ∈ H_ℓ, one has

$\Delta _{S^{n-1}}f=-\ell (\ell +n-2)f.$

where Δ_Sⁿ⁻¹ is the Laplace-Beltrami operator on Sⁿ⁻¹. This operator is the analog of the angular part of the Laplacian in three dimensions; to wit, the Laplacian in n dimensions decomposes as

$\nabla ^{2}=r^{1-n}{\frac {\partial }{\partial r}}r^{n-1}{\frac {\partial }{\partial r}}+r^{-2}\Delta _{S^{n-1}}.$

• It follows from the Stokes theorem and the preceding property that the spaces H_ℓ are orthogonal with respect to the inner product from L²(Sⁿ⁻¹). That is to say,

$\int _{S^{n-1}}f{\bar {g}}\,d\Omega =0$

for ƒ ∈ H_ℓ and g ∈ H_k for k ≠ ℓ.

• Conversely, the spaces H_ℓ are precisely the eigenspaces of Δ_Sⁿ⁻¹. In particular, an application of the spectral theorem to the Riesz potential $\Delta _{S^{n-1}}^{-1}$ gives another proof that the spaces H_ℓ are pairwise orthogonal and complete in L²(Sⁿ⁻¹).

Generalizations

The spherical harmonics map can be seen as representations of the symmetry group of rotations around a point (RO(3)) and its double-cover SU(2). As such they capture the symmetry of the two-dimensional sphere (or two-sphere). Each set of spherical harmonics with a given value for the l-parameter map onto a different irreducible representation of SO(3).

In addition, the two-sphere is equivalent to the Riemann sphere. The complete set of symmetries of the Riemann sphere are described by the Möbius transformation group PSL(2,C), which is isomorphic as a real Lie group to the Lorentz group. The analog of the spherical harmonics for the Lorentz group are given by the hypergeometric series; indeed, the spherical harmonics can be re-expressed in terms of the hypergeometric series, as SO(3) is a subgroup of PSL(2,C).

More generally, hypergeometric series can be generalized to describe the symmetries of any symmetric space; in particular, hypergeometric series can be developed for any Lie group.

See also

• Clebsch–Gordan coefficients
• Harmonic function
• Rotation group
• Sturm–Liouville theory
• Atomic orbital
• Solid harmonics
• Vector spherical harmonics
• Table of spherical harmonics

References

Cited references

General references

• E.W. Hobson, The Theory of Spherical and Ellipsoidal Harmonics, (1955) Chelsea Pub. Co., ISBN 978-0828401043.
• C. Müller, Spherical Harmonics, (1966) Springer, Lecture Notes in Mathematics, Vol. 17, ISBN 978-3-540-03600-5.
• A.R. Edmonds, Angular Momentum in Quantum Mechanics, (1957) Princeton University Press, ISBN 0-691-07912-9.
• E. U. Condon and G. H. Shortley, The Theory of Atomic Spectra, (1970) Cambridge at the University Press, ISBN 0-521-09209-4, See chapter 3.
• J.D. Jackson, Classical Electrodynamics, ISBN 0-471-30932-X
• Albert Messiah, Quantum Mechanics, volume II. (2000) Dover. ISBN 0-486-40924-4.
• D. A. Varshalovich, A. N. Moskalev, V. K. Khersonskii Quantum Theory of Angular Momentum,(1988) World Scientific Publishing Co., Singapore, ISBN 9971-5-0107-4
• Weisstein, Eric W. "Spherical harmonics". MathWorld.

External links

• Interactive calculator of spherical harmonics on Tal Carmon's Research Homepage
• Spherical harmonics applied to Acoustic Field analysis on Trinnov Audio's research page
• Spherical Harmonics by Stephen Wolfram and Nodal Domains of Spherical Harmonics by Michael Trott, the Wolfram Demonstrations Project
• An accessible introduction to spherical harmonics (by J. B. Calvert)
• Spherical harmonics entry at Citizendium
• OpenGL Spherical harmonics demo
• Allen McNamara's spherical harmonics animations
• Thorsten Becker's spherical harmonics animations

Software

• Spherical harmonics generator in OpenGL
• SHTOOLS: Fortran 95 software archive
• HEALPIX: Fortran 90 and C++ software archive
• SpherePack: Fortran 77 software archive
• SpharmonicKit: C software archive
• Frederik J Simons: Matlab software archive
• NFFT: C subroutine library (fast spherical Fourier transform for arbitrary nodes)
• Shansyn: spherical harmonics package for GMT/netcdf grd files
• SHAPE: Spherical HArmonic Parameterization Explorer