Area

For other uses, see the geometric quantity.

Area is a quantity expressing the two-dimensional size of a defined part of a surface, typically a region bounded by a closed curve. The term surface area refers to the total area of the exposed surface of a 3-dimensional solid, such as the sum of the areas of the exposed sides of a polyhedron. Area is an important invariant in the differential geometry of surfaces.

Units

Units for measuring area include:

area (a) = 100 square meters (m²)

hectare (ha) = 100 ares (a) = 10000 square meters (m²)

square kilometre (km²) = 100 hectars (ha) = 10000 ares (a) = 1000000 square metres (m²)

square megametre (Mm²) = 10¹² square metres

square foot = 144 square inches = 0.09290304 square metres (m²)

square yard = 9 square feet (0.84 m²) = 0.83612736 square metres (m²)

square perch = 30.25 square yards = 25.2928526 square metres (m²)

acre = 10 square chains (also one furlong by one chain); or 160 square perches; or 4840 square yards; or 43,560 square feet (4,047 m²) = 4046.8564224 square metres (m²)

square mile = 640 acres (2.6 km²) = 2.5899881103 square kilometers (km²)

Formulæ

Common formulæ for area:

Shape	Equation	Variables
Square	$s^{2}\,\!$	$s$ is the length of one side of the square.
Regular triangle (equilateral triangle)	${\frac {\sqrt {3}}{4}}s^{2}\,\!$	$s$ is the length of one side of the triangle.
Regular hexagon	${\frac {3{\sqrt {3}}}{2}}s^{2}\,\!$	$s$ is the length of one side of the hexagon.
Regular octagon	$2\left(1+{\sqrt {2}}\right)s^{2}\,\!$	$s$ is the length of one side of the octagon.
Any regular polygon	${\frac {1}{2}}ap\,\!$	$a$ is the apothem, or the radius of an inscribed circle in the polygon, and $p$ is the perimeter of the polygon.
Any regular polygon	${\frac {ns^{2}}{4\cdot \tan(\pi /n)}}\,\!$	$s$ is the sidelength and $n$ is the number of sides.
Any regular polygon (using degree measure)	${\frac {ns^{2}}{4\cdot \tan(180^{\circ }/n)}}\,\!$	$s$ is the sidelength and $n$ is the number of sides.
Rectangle	$lw\,\!$	$l$ and $w$ are the lengths of the rectangle's sides (length and width).
Parallelogram (in general)	$bh\,\!$	$b$ and $h$ are the length of the base and the length of the perpendicular height, respectively.
Rhombus	${\frac {1}{2}}ab$	$a$ and $b$ are the lengths of the two diagonals of the rhombus.
Triangle	${\frac {1}{2}}bh\,\!$	$b$ and $h$ are the base and altitude (measured perpendicular to the base), respectively.
Triangle	${\frac {1}{2}}ab\sin(C)\,\!$	$a$ and $b$ are any two sides, and $C$ is the angle between them.
Circle	$\pi r^{2}\ {\text{or}}\ {\frac {\pi d^{2}}{4}}\,\!$	$r$ is the radius and $d$ the diameter.
Ellipse	$\pi ab\,\!$	$a$ and $b$ are the semi-major and semi-minor axes, respectively.
Trapezoid	${\frac {1}{2}}(a+b)h\,\!$	$a$ and $b$ are the parallel sides and $h$ the distance (height) between the parallels.
Total surface area of a Cylinder	$2\pi r^{2}+2\pi rh\,\!$	$r$ and $h$ are the radius and height, respectively.
Lateral surface area of a cylinder	$2\pi rh\,\!$	$r$ and $h$ are the radius and height, respectively.
Total surface area of a Cone	$\pi r(l+r)\,\!$	$r$ and $l$ are the radius and slant height, respectively.
Lateral surface area of a cone	$\pi rl\,\!$	$r$ and $l$ are the radius and slant height, respectively.
Total surface area of a Sphere	$4\pi r^{2}\ {\text{or}}\ \pi d^{2}\,\!$	$r$ and $d$ are the radius and diameter, respectively.
Total surface area of an ellipsoid		See the article.
Circular sector	${\frac {1}{2}}r^{2}\theta \,\!$	$r$ and $\theta$ are the radius and angle (in radians), respectively.
Square to circular area conversion	${\frac {4}{\pi }}A\,\!$	$A$ is the area of the square in square units.
Circular to square area conversion	${\frac {1}{4}}C\pi \,\!$	$C$ is the area of the circle in circular units.

The above calculations show how to find the area of many common shapes.

The area of irregular polygons can be calculated using the "Surveyor's formula".

Additional formulæ

Areas of 2-dimensional figures

• a triangle: ${\frac {Bh}{2}}$ (where B is any side, and h is the distance from the line on which B lies to the other vertex of the triangle). This formula can be used if the height h is known. If the lengths of the three sides are known then Heron's formula can be used: ${\sqrt {s(s-a)(s-b)(s-c)}}$(where a, b, c are the sides of the triangle, and $s={\frac {a+b+c}{2}}$ is half of its perimeter) If an angle and its two included sides are given, then area=absinC where C is the given angle and a and b are its included sides. If the triangle is graphed on a coordinate plane, a matrix can be used and is simplified to the absolute value of (x₁y₂+ x₂y₃+ x₃y₁ - x₂y₁- x₃y₂- x₁y₃) all divided by 2. This formula is also known as the shoelace formula and is an easy way to solve for the area of a coordinate triangle by substituting the 3 points, (x₁,y₁) (x₂,y₂) (x₃,y ₃). The shoelace formula can also be used to find the areas of other polygons when their vertices are known. Another approach for a coordinate triangle is to use Infinitesimal calculus to find the area.

Area in calculus

The area between two graphs can be evaluated by calculating the difference between the integrals of the two functions

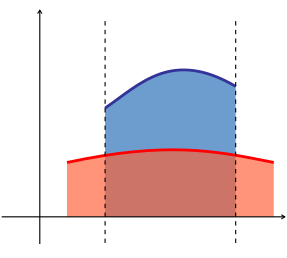
• the area between the graphs of two functions is equal to the integral of one function, f(x), minus the integral of the other function, g(x).
• an area bounded by a function r = r(θ) expressed in polar coordinates is ${1 \over 2}\int _{0}^{2\pi }r^{2}\,d\theta$.
• the area enclosed by a parametric curve ${\vec {u}}(t)=(x(t),y(t))$ with endpoints ${\vec {u}}(t_{0})={\vec {u}}(t_{1})$ is given by the line integrals

$\oint _{t_{0}}^{t_{1}}x{\dot {y}}\,dt=-\oint _{t_{0}}^{t_{1}}y{\dot {x}}\,dt={1 \over 2}\oint _{t_{0}}^{t_{1}}(x{\dot {y}}-y{\dot {x}})\,dt$

(see Green's theorem)

or the z-component of

${1 \over 2}\oint _{t_{0}}^{t_{1}}{\vec {u}}\times {\dot {\vec {u}}}\,dt.$

Surface area of 3-dimensional figures

• cube: $6s^{2}$, where s is the length of the top side
• rectangular box: $2(\ell w+\ell h+wh)$ the length divided by height
• cone: $\pi r\left(r+{\sqrt {r^{2}+h^{2}}}\right)$, where r is the radius of the circular base, and h is the height. That can also be rewritten as $\pi r^{2}+\pi rl$ where r is the radius and l is the slant height of the cone. $\pi r^{2}$ is the base area while $\pi rl$ is the lateral surface area of the cone.
• prism: 2 * Area of Base + Perimeter of Base * Height

General formula

The general formula for the surface area of the graph of a continuously differentiable function $z=f(x,y),$ where $(x,y)\in D\subset \mathbb {R} ^{2}$ and $D$ is a region in the xy-plane with the smooth boundary:

$A=\iint _{D}{\sqrt {\left({\frac {\partial f}{\partial x}}\right)^{2}+\left({\frac {\partial f}{\partial y}}\right)^{2}+1}}\,dx\,dy.$

Even more general formula for the area of the graph of a parametric surface in the vector form $\mathbf {r} =\mathbf {r} (u,v),$ where $\mathbf {r}$ is a continuously differentiable vector function of $(u,v)\in D\subset \mathbb {R} ^{2}$:

$A=\iint _{D}\left|{\frac {\partial \mathbf {r} }{\partial u}}\times {\frac {\partial \mathbf {r} }{\partial v}}\right|\,du\,dv.$

Area minimisation

Given a wire contour, the surface of least area spanning ("filling") it is a minimal surface. Familiar examples include soap bubbles.

The question of the filling area of the Riemannian circle remains open.

See also

• Equi-areal mapping
• Integral
• Orders of magnitude (area)—A list of areas by size.
• Volume

External links

• Area formulas
• Conversion cable diameter to circle cross-sectional area and vice versa