Regular polyhedron: Difference between revisions
| Line 43: | Line 43: | ||
|[[Image:Dodecadodecahedron.png|100px]]<br>[[Dodecadodecahedron]] |
|[[Image:Dodecadodecahedron.png|100px]]<br>[[Dodecadodecahedron]] |
||
|[[Image:Excavated dodecahedron.png|100px]]<br>[[Excavated dodecahedron]] |
|[[Image:Excavated dodecahedron.png|100px]]<br>[[Excavated dodecahedron]] |
||
|[[Image: |
|[[Image:DU36 medial rhombic triacontahedron.png|100px]]<br>[[Medial rhombic triacontahedron]] |
||
|[[Image:DU41 medial triambic icosahedron.png|100px]]<br>[[Medial triambic icosahedron]] |
|[[Image:DU41 medial triambic icosahedron.png|100px]]<br>[[Medial triambic icosahedron]] |
||
|- align=center |
|- align=center |
||
Revision as of 09:20, 31 August 2011
A regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags. This last alone is a sufficient definition.
A regular polyhedron is identified by its Schläfli symbol of the form {n, m}, where n is the number of sides of each face and m the number of faces meeting at each vertex.
The regular polyhedra
There are five convex regular polyhedra, known as the Platonic solids:


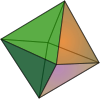


Tetrahedron {3, 3} Cube {4, 3} Octahedron {3, 4} Dodecahedron {5, 3} Icosahedron {3, 5}
and four regular star polyhedra, the Kepler-Poinsot polyhedra:




Small stellated dodecahedron
{5/2, 5}Great stellated dodecahedron
{5/2, 3}Great dodecahedron
{5, 5/2}Great icosahedron
{3, 5/2}
Topological regular polyhedra
Topologically, there are five other regular polyhedra, but they require distortion to be immersed in three-dimensional Euclidean space. They are all topologically equivalent to hyperbolic planes.
Polyhedron 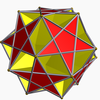
Ditrigonal dodecadodecahedron
Dodecadodecahedron
Excavated dodecahedron
Medial rhombic triacontahedron
Medial triambic icosahedronTiling 
{5, 6}
{5, 4}
{6, 6}
{4, 5}
{6, 5}
These regular polyhedra were identified by H. S. M. Coxeter in his book Regular Polytopes (1977) and again by J. M. Wills in his paper "The combinatorially regular polyhedra of index 2" (1987).[1]
The tiling images have colours corresponding to those of the polyhedra images (except for the ditrigonal dodecadodecahedron, where the correct image is not available yet).
Characteristics
Equivalent properties
The property of having a similar arrangement of faces around each vertex can be replaced by any of the following equivalent conditions in the definition:
- The vertices of the polyhedron all lie on a sphere.
- All the dihedral angles of the polyhedron are equal.
- All the vertex figures of the polyhedron are regular polygons.
- All the solid angles of the polyhedron are congruent. (Cromwell, 1997)
Concentric spheres
A regular polyhedron has all of three related spheres (other polyhedra lack at least one kind) which share its centre:
- An insphere, tangent to all faces.
- An intersphere or midsphere, tangent to all edges.
- A circumsphere, tangent to all vertices.
Symmetry
The regular polyhedra are the most symmetrical of all the polyhedra. They lie in just three symmetry groups, which are named after them:
- Tetrahedral
- Octahedral (or cubic)
- Icosahedral (or dodecahedral)
Any shapes with icosahedral or octahedral symmetry will also contain tetrahedral symmetry.
Euler characteristic
The five Platonic solids have an Euler characteristic of 2. Some of the regular stars have a different value.
Duality of the regular polyhedra
The regular polyhedra come in natural pairs, with each twin being dual to the other (i.e. the vertices of one polyhedron correspond to the faces of the other, and vice versa):
- The tetrahedron is self-dual, i.e. it pairs with itself.
- The cube and octahedron are dual to each other.
- The icosahedron and dodecahedron are dual to each other.
- The small stellated dodecahedron and great dodecahedron are dual to each other.
- The great stellated dodecahedron and great icosahedron are dual to each other.
Among the topologically regular polyhedra:
- The excavated dodecahedron is self-dual.
- The dodecadodecahedron and medial rhombic triacontahedron are dual to each other.
- The ditrigonal dodecadodecahedron and medial triambic icosahedron are dual to each other.
The Schläfli symbol of the dual is just the original written backwards, for example the dual of {5, 3} is {3, 5}.
For further information please see the individual articles or the general polyhedron article.
History
See also Regular polytope: History of discovery.
Prehistory
Stones carved in shapes showing the symmetry of all five of the Platonic solids have been found in Scotland and may be as much as 4,000 years old. These stones show not only the form of each of the five Platonic solids, but also the relations of duality amongst them (that is, that the centres of the faces of the cube gives the vertices of an octahedron, and so on). Examples of these stones are on display in the John Evans room of the Ashmolean Museum at Oxford University. Why these objects were made, or how their creators gained the inspiration for them, is a mystery.
It is also possible that the Etruscans preceded the Greeks in their awareness of at least some of the regular polyhedra, as evidenced by the discovery near Padua (in Northern Italy) in the late 19th century of a dodecahedron made of soapstone, and dating back more than 2,500 years (Lindemann, 1987). Pyritohedric crystals are found in northern Italy[citation needed].
Greeks
The earliest known written records of the regular convex solids originated from Classical Greece. When these solids were all discovered and who by is not known, but Theaetetus, (an Athenian), was the first to give a mathematical description of all five (Van der Waerden, 1954), (Euclid, book XIII). H.S.M. Coxeter (Coxeter, 1948, Section 1.9) credits Plato (400 BC) with having made models of them, and mentions that one of the earlier Pythagoreans, Timaeus of Locri, used all five in a correspondence between the polyhedra and the nature of the universe as it was then perceived - this correspondence is recorded in Plato's dialogue Timaeus. Euclid's reference to Plato led to their common description as the Platonic solids.
One might characterise the Greek definition as follows:
- A regular polygon is a (convex) planar figure with all edges equal and all corners equal
- A regular polyhedron is a solid (convex) figure with all faces being congruent regular polygons, the same number arranged all alike around each vertex.
This definition rules out, for example, the square pyramid (since although all the faces are regular, the square base is not congruent to the triangular sides), or the shape formed by joining two tetrahedra together (since although all faces of that triangular bipyramid would be equilateral triangles, that is, congruent and regular, some vertices have 3 triangles and others have 4).
This concept of a regular polyhedron would remain unchallenged for almost 2000 years.
Regular star polyhedra
Regular star polygons such as the pentagram (star pentagon) were also known to the ancient Greeks - the pentagram was used by the Pythagoreans as their secret sign, but they did not use them to construct polyhedra. It was not until the early 17th century that Johannes Kepler realised that pentagrams could be used as the faces of regular star polyhedra. Some of these star polyhedra may have been discovered by others before Kepler's time, but Kepler was the first to recognise that they could be considered "regular" if one removed the restriction that regular polyhedra be convex. Two hundred years later Louis Poinsot also allowed star vertex figures (circuits around each corner), enabling him to discover two new regular star polyhedra along with rediscovering Kepler's. These four are the only regular star polyhedra, and have come to be known as the the Kepler-Poinsot polyhedra. It was not until the mid-19th century, several decades after Poinsot published, that Cayley gave them their modern English names: (Kepler's) small stellated dodecahedron and great stellated dodecahedron, and (Poinsot's) great icosahedron and great dodecahedron.
The Kepler-Poinsot polyhedra may be constructed from the Platonic solids by a process called stellation. The reciprocal process to stellation is called facetting (or faceting). Every stellation of one polyhedron is dual, or reciprocal, to some facetting of the dual polyhedron. The regular star polyhedra can also be obtained by facetting the Platonic solids. This was first done by Bertrand around the same time that Cayley named them.
By the end of the 19th century there were therefore nine regular polyhedra - five convex and four star.
Further generalisations
The 20th century saw a succession of generalisations of the idea of a regular polyhedron, leading to several new classes.
In the first decades, Coxeter and Petrie allowed "saddle" vertices with alternating ridges and valleys, enabling them to construct three infinite folded surfaces which they called regular skew polyhedra.
Studies of non-Euclidean hyperbolic, elliptic and complex spaces, discovered much earlier, led to the further discovery of new polyhedra such as complex polyhedras which could only take regular form in those spaces.
By now, polyhedra were firmly understood as three-dimensional examples of more general polytopes in any number of dimensions. The second half of the century saw the development of abstract algebraic ideas such as Polyhedral combinatorics, culminating in the idea of an abstract polytope as a partially ordered set (poset) of elements. The elements of an abstract polyhedron are its body (the maximal element), its faces, edges, vertices and the null polytope or empty set. Abstract regular polytopes remain an active area of research.
Regular polyhedra in nature
Each of the Platonic solids occurs naturally in one form or another.
The tetrahedron, cube, and octahedron all occur as crystals. These by no means exhaust the numbers of possible forms of crystals (Smith, 1982, p212), of which there are 48. Neither the regular icosahedron nor the regular dodecahedron are amongst them, although one of the forms, called the pyritohedron, has twelve pentagonal faces arranged in the same pattern as the faces of the regular dodecahedron. The faces of the pyritohedron are, however, not regular, so the pyritohedron is also not regular.
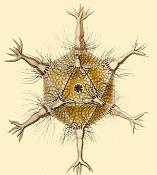
Polyhedra appear in biology as well. In the early 20th century, Ernst Haeckel described a number of species of Radiolaria, some of whose skeletons are shaped like various regular polyhedra. (Haeckel, 1904) Examples include Circoporus octahedrus, Circogonia icosahedra, Lithocubus geometricus and Circorrhegma dodecahedra; the shapes of these creatures are indicated by their names. The outer protein shells of many viruses form regular polyhedra. For example, HIV is enclosed in a regular icosahedron.
A more recent discovery is of a series of new types of carbon molecule, known as the fullerenes (see (Curl, 1991) for an exposition of this discovery). Although C60, the most easily produced fullerene, looks more or less spherical, some of the larger varieties (such as C240, C480 and C960) are hypothesised to take on the form of slightly rounded icosahedra, a few nanometres across.
In ancient times the Pythagoreans believed that there was a harmony between the regular polyhedra and the orbits of the planets. In the 17th century, Johannes Kepler studied data on planetary motion compiled by Tycho Brahe and for a decade tried to establish the Pythagorean ideal by finding a match between the sizes of the polyhedra and the sizes of the planets' orbits. His search failed in its original objective, but out of this research came Kepler's discoveries of the Kepler solids as regular polytopes, the realisation that the orbits of planets are not circles, and the laws of planetary motion for which he is now famous. In Kepler's time only five planets (excluding the earth) were known, nicely matching the number of Platonic solids. Kepler's work, and the discovery since that time of Uranus and Neptune, have invalidated the Pythagorean idea.
Around the same time as the Archimedeans, Plato described a theory of matter in which the five elements (earth, air, fire, water and spirit) each comprised one of the five regular solids. Matter was built up from many tiny copies of these polyhedra. Two thousand years later, Dalton's atomic theory would show this idea to be along the right lines, but not related directly to the regular solids.
See also
References
- Bertrand, J. (1858). Note sur la théorie des polyèdres réguliers, Comptes rendus des séances de l'Académie des Sciences, 46, pp. 79–82.
- Cromwell, Peter R. (1997). Polyhedra. Cambridge University Press. p. 77. ISBN 0-521-66405-5.
- Haeckel, E. (1904). Kunstformen der Natur. Available as Haeckel, E. Art forms in nature, Prestel USA (1998), ISBN 3-7913-1990-6, or online at http://caliban.mpiz-koeln.mpg.de/~stueber/haeckel/kunstformen/natur.html
- Smith, J. V. (1982). Geometrical And Structural Crystallography. John Wiley and Sons.
- Sommerville, D. M. Y. (1930). An Introduction to the Geometry of n Dimensions. E. P. Dutton, New York. (Dover Publications edition, 1958). Chapter X: The Regular Polytopes.
- ^ The Regular Polyhedra (of index two), David A. Richter



















