Fibonacci sequence: Difference between revisions
←Replaced content with 'fibonacci is gay so so so gay' Tag: blanking |
ClueBot NG (talk | contribs) m Reverting possible vandalism by 87.36.48.16 to version by TheRingess. False positive? Report it. Thanks, ClueBot NG. (564387) (Bot) |
||
| Line 1: | Line 1: | ||
[[File:FibonacciBlocks.svg|thumb|180px|right|A tiling with squares whose sides are successive Fibonacci numbers in length]] |
|||
fibonacci is gay |
|||
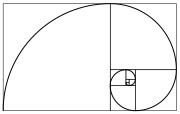
[[File:Fibonacci spiral 34.svg|right|thumb|180px|A Fibonacci spiral created by drawing circular arcs connecting the opposite corners of squares in the Fibonacci tiling; this one uses squares of sizes 1, 1, 2, 3, 5, 8, 13, 21, and 34. See [[golden spiral]].]] |
|||
In [[mathematics]], the '''Fibonacci numbers''' are the numbers in the following [[integer sequence]]: |
|||
:<math>0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\;</math> {{OEIS|id=A000045}}. |
|||
By definition, the first two Fibonacci numbers are 0 and 1, and each subsequent number is the sum of the previous two. |
|||
In mathematical terms, the sequence ''F<sub>n</sub>'' of Fibonacci numbers is defined by the [[recurrence relation]] |
|||
:<math>F_n = F_{n-1} + F_{n-2},\!\,</math> |
|||
with seed values |
|||
:<math>F_0 = 0 \quad\text{and}\quad F_1 = 1.</math><ref>Lucas p. 3</ref> |
|||
The Fibonacci sequence is named after [[Leonardo of Pisa]], who was known as Fibonacci. Fibonacci's 1202 book ''[[Liber Abaci]]'' introduced the sequence to Western European mathematics,<ref name="Sigler"/> although the sequence had been described earlier in [[Indian mathematics]].<ref name="GlobalScience"/><ref name="HistoriaMathematica"/><ref name="Donald Knuth 2006 50"/> |
|||
(By modern convention, the sequence begins with ''F''<sub>0</sub> = 0. The ''Liber Abaci'' began the sequence with ''F''<sub>1</sub> = 1, omitting the initial 0, and the sequence is still written this way by some.) |
|||
Fibonacci numbers are closely related to [[Lucas number]]s in that they are a complementary pair of [[Lucas sequence]]s. They are intimately connected with the [[golden ratio]], for example the [[closest rational approximation]]s to the ratio are 2/1, 3/2, 5/3, 8/5, ... . Applications include computer algorithms such as the [[Fibonacci search technique]] and the [[Fibonacci heap]] data structure, and graphs called [[Fibonacci cube]]s used for interconnecting parallel and distributed systems. They also appear in biological settings,<ref name="S. Douady and Y. Couder 1996 255–274">{{Cite journal|author=S. Douady and Y. Couder |title=Phyllotaxis as a Dynamical Self Organizing Process |journal=Journal of Theoretical Biology |year=1996 |issue=178 |pages= 255–274 |url=http://www.math.ntnu.no/~jarlet/Douady96.pdf |doi = 10.1006/jtbi.1996.0026 |volume=178 |format=PDF}}</ref> such as branching in trees, [[Phyllotaxis|arrangement of leaves on a stem]], the fruit spouts of a [[pineapple]],<ref name="Jones 2006 544">{{Cite book|first=Judy |last=Jones |coauthors=William Wilson |title=An Incomplete Education |publisher=Ballantine Books |year=2006 |isbn=978-0-7394-7582-9 |page=544 |chapter=Science}}</ref> the flowering of [[artichoke]], an uncurling [[fern]] and the arrangement of a [[pine cone]].<ref name="A. Brousseau 1969 525–532">{{Cite journal|author=A. Brousseau |title=Fibonacci Statistics in Conifers |journal=[[Fibonacci Quarterly]] |year=1969 |issue=7 |pages= 525–532}}</ref> |
|||
==Origins== |
|||
The Fibonacci sequence appears in [[Indian mathematics]], in connection with [[Sanskrit prosody]].<ref name="HistoriaMathematica">{{Cite journal|first=Parmanand|last=Singh|title=The So-called Fibonacci numbers in ancient and medieval India|journal=Historia Mathematica|volume=12|issue=3|pages=229–244|year=1985|doi=10.1016/0315-0860(85)90021-7}} |
|||
</ref><ref name=knuth-v1> |
|||
{{cite book |
|||
|title=The Art Of Computer Programming, Volume 1 |
|||
|author=[[Donald Knuth]] |
|||
|publisher=Addison Wesley |
|||
|year=1968 |
|||
|isbn=8177587544 |
|||
|url=http://books.google.com/?id=MooMkK6ERuYC&pg=PA100&dq=knuth+gopala+fibonacci#v=onepage& |
|||
}}quote: |
|||
"Before Fibonacci wrote his work, the sequence Fn had already been discussed |
|||
by Indian scholars, who had long been interested in rhythmic |
|||
patterns... both Gopala (before 1135AD) and Hemachandra (c.1150) mentioned |
|||
the numbers 1,2,3,5,8,13,21 explicitly. [See P. Singh Historia Math 12 |
|||
(1985) 229–244]" p. 100 (3d ed)...</ref> In the Sanskrit oral tradition, there was much emphasis on how long (L) syllables mix with the short (S), and counting the different patterns of L and S within a given fixed length results in the Fibonacci numbers; the number of patterns that are ''m'' short syllables long is the Fibonacci number ''F''<sub>''m'' + 1</sub>.<ref name="Donald Knuth 2006 50">{{Cite book|title = The Art of Computer Programming: Generating All Trees—History of Combinatorial Generation; Volume 4 |author=Donald Knuth |publisher=Addison–Wesley |year=2006 |isbn=9780321335708 | page=50 |url=http://books.google.com/?id=56LNfE2QGtYC&pg=PA50&dq=rhythms}} |
|||
quote: |
|||
it was natural to consider the set of all sequences of [L] and [S] that |
|||
have exactly m beats. ... there are exactly Fm+1 of them. For example the 21 |
|||
sequences when ''m'' = 7 are: [gives list]. |
|||
In this way Indian prosodists were led to discover the Fibonacci sequence, as |
|||
we have observed in Section 1.2.8 (from v.1)</ref> |
|||
Susantha Goonatilake writes that the development of the Fibonacci sequence "is attributed in part to [[Pingala]] (200 BC), later being associated with [[Virahanka]] (c. 700 AD), [[Gopala (mathematician)|Gopāla]] (c.1135 AD), and [[Hemachandra]] (c.1150)".<ref name="GlobalScience">{{Cite book|title =Toward a Global Science | author = Susantha Goonatilake |publisher = Indiana University Press |year = 1998 |page = 126 |isbn = 9780253333889 |url =http://books.google.com/?id=SI5ip95BbgEC&pg=PA126&dq=Virahanka+Fibonacci |
|||
}}</ref> Parmanand Singh cites Pingala's cryptic formula ''misrau cha'' ("the two are mixed") and cites scholars who interpret it in context as saying that the cases for ''m'' beats (''F''<sub>''m''</sub>) is obtained by adding a [S] to ''F''<sub>''m''−1</sub> cases and [L] to the ''F''<sub>''m''−2</sub> cases. He dates Pingala before 450 BCE.<ref>[Agrawala. V. S. 1969]. pAninikAlIna bhAratavarSha (Hn.). Varanasi-I: TheChowkhamba Vidyabhawan. |
|||
<!-- |
|||
quote:SadgurushiShya writes |
|||
that Pingala was a younger brother of Panini [Agrawala 1969, lb]. There is |
|||
an alternative opinion that he was a maternal uncle of Panini [Vinayasagar |
|||
1965, Preface, 121. |
|||
... Agrawala [1969, 463–476[, after a careful investigation in which |
|||
he considered the views of earlier scholars. has concluded that PAnini |
|||
lived between 480 and 410 B.C. |
|||
--> |
|||
</ref> |
|||
However, the clearest exposition of the series arises in the work of [[Virahanka]] (c. 700AD), whose own work is lost, but is available in a quotation by Gopala (c.1135): |
|||
: Variations of two earlier meters [is the variation]... For example, for [a meter of length] four, variations of meters of two [and] three being mixed, five happens. [works out examples 8, 13, 21]... In this way, the process should be followed in all ''mAtrA-vr.ttas'' (prosodic combinations).<ref>{{cite book |
|||
|author = Velankar, H. D. |
|||
|year = 1962. |
|||
|title = _Vr^ttajAtisamuccaya_ of kavi Virahanka |
|||
|publisher = Rajasthan Oriental Research Institute, Jodhpur |
|||
}} p.101. quote: " |
|||
For four, variations of meters of two [and] three being mixed, five happens. |
|||
For five, variations of two earlier – three [and] four, being mixed, eight is obtained. |
|||
:In this way, for six, [variations] of four [and] of five being mixed, thirteen happens. And like that, variations of two earlier meters being mixed, seven morae [is] twenty-one. In this way, the process should be |
|||
followed in all mAtrA-vr^ttas.</ref> |
|||
The series is also discussed by Gopala (before 1135AD) and by the Jain scholar Hemachandra (c. 1150AD). |
|||
In the West, the Fibonacci sequence first appears in the book [[Liber Abaci]] (1202) by Leonardo of Pisa, known as [[Fibonacci]].<ref name=Sigler>{{Cite book|title = Fibonacci's Liber Abaci |author = Sigler, Laurence E. (trans.) |publisher = Springer-Verlag |year = 2002 |isbn = 0-387-95419-8}} Chapter II.12, pp. 404–405.</ref> Fibonacci considers the growth of an idealized (biologically unrealistic) [[rabbit]] population, assuming that: a newly born pair of rabbits, one male, one female, are put in a field; rabbits are able to mate at the age of one month so that at the end of its second month a female can produce another pair of rabbits; rabbits never die and a mating pair always produces one new pair (one male, one female) every month from the second month on. The puzzle that Fibonacci posed was: how many pairs will there be in one year? |
|||
so so so gay |
|||
* At the end of the first month, they mate, but there is still only 1 pair. |
|||
* At the end of the second month the female produces a new pair, so now there are 2 pairs of rabbits in the field. |
|||
* At the end of the third month, the original female produces a second pair, making 3 pairs in all in the field. |
|||
* At the end of the fourth month, the original female has produced yet another new pair, the female born two months ago produces her first pair also, making 5 pairs. |
|||
At the end of the ''n''th month, the number of pairs of rabbits is equal to the number of new pairs (which is the number of pairs in month ''n'' − 2) plus the number of pairs alive last month (''n'' − 1). This is the ''n''th Fibonacci number.<ref>{{cite web |
|||
| last = Knott |
|||
| first = Ron |
|||
| title = Fibonacci's Rabbits |
|||
| url=http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibnat.html#Rabbits |
|||
| publisher =[[University of Surrey]] Faculty of Engineering and Physical Sciences}}</ref> |
|||
The name "Fibonacci sequence" was first used by the 19th-century number theorist [[Édouard Lucas]].<ref>{{cite book |
|||
|author = [[Martin Gardner]] |
|||
|title=Mathematical Circus |
|||
|publisher = The Mathematical Association of America |
|||
|year=1996 |
|||
|isbn= 0883855062}}quote: |
|||
"It is ironic that Leonardo, who made valuable contributions to mathematics, |
|||
is remembered today mainly because a 19th-century French number theorist, |
|||
Edouard Lucas ... attached the name Fibonacci to a number sequence that appears |
|||
in a trivial problem in Liber abaci." p.153</ref> |
|||
==List of Fibonacci numbers== |
|||
The first 21 Fibonacci numbers ''F<sub>n</sub>'' for ''n'' = 0, 1, 2, ..., 20 are:<ref>The website [http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibtable.html] has the first 300 F<sub>''n''</sub> factored into primes and links to more extensive tables.</ref> |
|||
:{| class="wikitable" style="text-align:right" |
|||
|- |
|||
| ''F''<sub>0</sub> |
|||
| ''F''<sub>1</sub> |
|||
| ''F''<sub>2</sub> |
|||
| ''F''<sub>3</sub> |
|||
| ''F''<sub>4</sub> |
|||
| ''F''<sub>5</sub> |
|||
| ''F''<sub>6</sub> |
|||
| ''F''<sub>7</sub> |
|||
| ''F''<sub>8</sub> |
|||
| ''F''<sub>9</sub> |
|||
| ''F''<sub>10</sub> |
|||
| ''F''<sub>11</sub> |
|||
| ''F''<sub>12</sub> |
|||
| ''F''<sub>13</sub> |
|||
| ''F''<sub>14</sub> |
|||
| ''F''<sub>15</sub> |
|||
| ''F''<sub>16</sub> |
|||
| ''F''<sub>17</sub> |
|||
| ''F''<sub>18</sub> |
|||
| ''F''<sub>19</sub> |
|||
| ''F''<sub>20</sub> |
|||
|- |
|||
| 0 |
|||
| 1 |
|||
| 1 |
|||
| 2 |
|||
| 3 |
|||
| 5 |
|||
| 8 |
|||
| 13 |
|||
| 21 |
|||
| 34 |
|||
| 55 |
|||
| 89 |
|||
| 144 |
|||
| 233 |
|||
| 377 |
|||
| 610 |
|||
| 987 |
|||
| 1597 |
|||
| 2584 |
|||
| 4181 |
|||
| 6765 |
|||
|} |
|||
The sequence can also be extended to negative index ''n'' using the re-arranged recurrence relation |
|||
:<math>F_{n-2} = F_n - F_{n-1}, \, </math> |
|||
{{anchor|Negafibonacci}} which yields the sequence of "negafibonacci" numbers<ref>Knuth, Donald. "Negafibonacci Numbers and the Hyperbolic Plane" Paper presented at the annual meeting of the Mathematical Association of America, The Fairmont Hotel, San Jose, CA. 2008-12-11 <http://www.allacademic.com/meta/p206842_index.html></ref> satisfying |
|||
:<math>F_{-n} = (-1)^{n+1} F_n. \, </math> |
|||
Thus the complete sequence is |
|||
:{| class="wikitable" style="text-align:right" |
|||
|- |
|||
| ''F''<sub>−8</sub> |
|||
| ''F''<sub>−7</sub> |
|||
| ''F''<sub>−6</sub> |
|||
| ''F''<sub>−5</sub> |
|||
| ''F''<sub>−4</sub> |
|||
| ''F''<sub>−3</sub> |
|||
| ''F''<sub>−2</sub> |
|||
| ''F''<sub>−1</sub> |
|||
| ''F''<sub>0</sub> |
|||
| ''F''<sub>1</sub> |
|||
| ''F''<sub>2</sub> |
|||
| ''F''<sub>3</sub> |
|||
| ''F''<sub>4</sub> |
|||
| ''F''<sub>5</sub> |
|||
| ''F''<sub>6</sub> |
|||
| ''F''<sub>7</sub> |
|||
| ''F''<sub>8</sub> |
|||
|- |
|||
| −21 |
|||
| 13 |
|||
| −8 |
|||
| 5 |
|||
| −3 |
|||
| 2 |
|||
| −1 |
|||
| 1 |
|||
| 0 |
|||
| 1 |
|||
| 1 |
|||
| 2 |
|||
| 3 |
|||
| 5 |
|||
| 8 |
|||
| 13 |
|||
| 21 |
|||
|} |
|||
==Occurrences in mathematics== |
|||
[[File:PascalTriangleFibanacci.svg|thumb|right|360px|The Fibonacci numbers are the sums of the "shallow" diagonals (shown in red) of [[Pascal's triangle]].]] |
|||
The Fibonacci numbers occur in the sums of "shallow" diagonals in [[Pascal's triangle]] (''see [[Binomial coefficient]]'').<ref>Lucas p. 7</ref> |
|||
The Fibonacci numbers can be found in different ways in the sequence of [[binary numeral system|binary]] [[String (computer science)|strings]]. |
|||
* The number of binary strings of length ''n'' without consecutive 1s is the Fibonacci number ''F''<sub>''n''+2</sub>. For example, out of the 16 binary strings of length 4, there are ''F''<sub>6</sub> = 8 without consecutive 1s – they are 0000, 1000, 0100, 0010, 1010, 0001, 1001 and 0101. By symmetry, the number of strings of length ''n'' without consecutive 0s is also ''F''<sub>''n''+2</sub>. |
|||
* The number of binary strings of length ''n'' without an odd number of consecutive 1s is the Fibonacci number ''F''<sub>''n+1''</sub>. For example, out of the 16 binary strings of length 4, there are ''F''<sub>5</sub> = 5 without an odd number of consecutive 1s – they are 0000, 0011, 0110, 1100, 1111. |
|||
* The number of binary strings of length ''n'' without an even number of consecutive 0s or 1s is 2''F''<sub>''n''</sub>. For example, out of the 16 binary strings of length 4, there are 2''F''<sub>4</sub> = 6 without an even number of consecutive 0s or 1s – they are 0001, 1000, 1110, 0111, 0101, 1010. |
|||
==Relation to the golden ratio== |
|||
===Closed-form expression=== |
|||
Like every sequence defined by linear [[Recurrence relation|recurrence]],<ref>{{Cite document|contribution=2.1.1 Constant coefficients – A) Homogeneous equations|title=Mathematics for the Analysis of Algorithms|first1=Daniel H.|last1=Greene|first2=Donald E.|last2=Knuth|author2-link=Donald Knuth|edition=2nd|publisher=Birkhäuser|page=17|year=1982}}</ref> the Fibonacci numbers have a [[closed form expression|closed-form solution]]. It has become very well known as '''[[Jacques Philippe Marie Binet|Binet]]'s formula''', even though it was already known by [[Abraham de Moivre]]:{{Citation needed|date=May 2011}} |
|||
:<math>F_n = \frac{\varphi^n-\psi^n}{\varphi-\psi} = \frac{\varphi^n-\psi^n}{\sqrt 5}</math> |
|||
where |
|||
:<math>\varphi = \frac{1 + \sqrt{5}}{2} \approx 1.61803\,39887\dots\,</math> |
|||
is the [[golden ratio]] {{OEIS|id=A001622}}, and |
|||
:<math>\psi = \frac{1 - \sqrt{5}}{2} = 1 - \varphi = - {1 \over \varphi}.</math><ref>Ball p. 156</ref> |
|||
To see this,<ref>Following Ball p. 155-156</ref> note that φ and ψ are both solutions of the equations |
|||
:<math>x^2=x+1,\,x^n=x^{n-1}+x^{n-2},\,</math> |
|||
so the powers of φ and ψ satisfy the Fibonacci recursion. In other words |
|||
:<math>\varphi^n = \varphi^{n-1} + \varphi^{n-2}\, </math> |
|||
and |
|||
:<math>\psi^n = \psi^{n-1} + \psi^{n-2}\, .</math> |
|||
It follows that for any values ''a'' and ''b'', the sequence defined by |
|||
:<math>U_n=a \varphi^n + b \psi^n</math> |
|||
satisfies the same recurrence |
|||
:<math>U_n=a \varphi^{n-1} + b \psi^{n-1} + a \varphi^{n-2} + b \psi^{n-2}=U_{n-1}+U_{n-2}.\,</math> |
|||
If ''a'' and ''b'' are chosen so that ''U''<sub>0</sub> = 0 and ''U''<sub>1</sub> = 1 then the resulting sequence ''U''<sub>''n''</sub> must be the Fibonacci sequence. This is the same as requiring ''a'' and ''b'' satisfy the system of equations: |
|||
:<math>a+b=0\,</math> |
|||
:<math>\varphi a + \psi b = 1\,</math> |
|||
which has solution |
|||
:<math>a=1/(\varphi-\psi)=1/\sqrt 5,\, b=-a</math> |
|||
producing the required formula. |
|||
===Computation by rounding=== |
|||
Since |
|||
:<math>|\psi|^n/\sqrt 5 < 1/2</math> |
|||
for all ''n'' ≥ 0, the number ''F''<sub>''n''</sub> is the closest integer to |
|||
:<math>\varphi^n/\sqrt 5\, .</math> |
|||
Therefore it can be found by [[Rounding#Exact computation with rounded arithmetic|rounding]], or in terms of the [[floor function]]: |
|||
:<math>F_n=\bigg\lfloor\frac{\varphi^n}{\sqrt 5} + \frac{1}{2}\bigg\rfloor,\ n \geq 0.</math> |
|||
Similarly, if we already know that the number ''F'' > 1 is a Fibonacci number, we can determine its index within the sequence by |
|||
:<math>n(F) = \bigg\lfloor \log_\varphi \left(F\cdot\sqrt{5} + \frac{1}{2}\right) \bigg\rfloor</math> |
|||
===Limit of consecutive quotients=== |
|||
[[Johannes Kepler]] observed that the ratio of consecutive Fibonacci numbers converges. He wrote that "as 5 is to 8 so is 8 to 13, practically, and as 8 is to 13, so is 13 to 21 almost", and concluded that the limit approaches the golden ratio <math>\varphi\,</math>.<ref>{{Cite book|last=Kepler |first=Johannes |title=A New Year Gift: On Hexagonal Snow |year=1966 |isbn=0198581203 |publisher=Oxford University Press |page=92}} Strena seu de Nive Sexangula (1611).</ref> |
|||
:<math>\lim_{n\to\infty}\frac{F_{n+1}}{F_n}=\varphi</math> |
|||
This convergence does not depend on the starting values chosen, excluding 0, 0. For example, the initial values 19 and 31 generate the sequence 19, 31, 50, 81, 131, 212, 343, 555 ... etc. The ratio of consecutive terms in this sequence shows the same convergence towards the golden ratio. |
|||
In fact this holds for any sequence which satisfies the Fibonacci recurrence other than a sequence of 0's. This can be derived from Binet's formula. |
|||
===Decomposition of powers of the golden ratio=== |
|||
Since the golden ratio satisfies the equation |
|||
:<math>\varphi^2=\varphi+1,\,</math> |
|||
this expression can be used to decompose higher powers <math>\varphi^n</math> as a linear function of lower powers, which in turn can be decomposed all the way down to a linear combination of <math>\varphi\, </math> and 1. The resulting [[recurrence relation]]ships yield Fibonacci numbers as the linear coefficients: |
|||
:<math>\varphi^n=F(n)\varphi+F(n-1).</math> |
|||
This expression is also true for <math>n \, <\, 1 \, </math> if the Fibonacci sequence <math>F(n) \,</math> is [[Generalizations of Fibonacci numbers#Extension to negative integers|extended to negative integers]] using the Fibonacci rule <math>F(n) = F(n-1) + F(n-2) . \, </math> |
|||
==Matrix form== |
|||
A 2-dimensional system of linear [[difference equations]] that describes the Fibonacci sequence is |
|||
:<math>{F_{k+2} \choose F_{k+1}} = \begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix} {F_{k+1} \choose F_{k}}</math> |
|||
or |
|||
:<math>\vec F_{k+1} = A \vec F_{k}\,.</math> |
|||
The [[eigenvalue]]s of the matrix A are <math>\varphi\,\!</math> and <math>(1-\varphi)\,\!</math>, and the elements of the [[eigenvector]]s of A, <math>{\varphi \choose 1}</math> and <math>{1 \choose -\varphi}</math>, are in the ratios <math>\varphi\,\!</math> and <math>(1-\varphi\,\!).</math> Using these facts, and the properties of eigenvalues, we can derive a direct formula for the nth element in the fibonacci series: |
|||
:<math>F_{n} = \cfrac{1}{\sqrt{5}}\cdot\left(\cfrac{1+\sqrt{5}}{2}\right)^n-\cfrac{1}{\sqrt{5}}\cdot\left(\cfrac{1-\sqrt{5}}{2}\right)^n.</math> |
|||
The matrix has a [[determinant]] of −1, and thus it is a 2×2 [[unimodular matrix]]. This property can be understood in terms of the [[continued fraction]] representation for the golden ratio: |
|||
:<math>\varphi |
|||
=1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{\;\;\ddots\,}}} \;. </math> |
|||
The Fibonacci numbers occur as the ratio of successive convergents of the continued fraction for <math>\varphi\,\!</math>, and the matrix formed from successive convergents of any continued fraction has a determinant of +1 or −1. |
|||
The matrix representation gives the following [[closed expression]] for the Fibonacci numbers: |
|||
:<math>\begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix}^n = |
|||
\begin{pmatrix} F_{n+1} & F_n \\ |
|||
F_n & F_{n-1} \end{pmatrix}. |
|||
</math> |
|||
Taking the determinant of both sides of this equation yields [[Cassini's identity]] |
|||
:<math>(-1)^n = F_{n+1}F_{n-1} - F_n^2\,.</math> |
|||
Additionally, since <math> A^n A^m=A^{m+n}</math> for any square matrix ''A'', the following identities can be derived: |
|||
:<math>{F_m}{F_n} + {F_{m-1}}{F_{n-1}} = F_{m+n-1}\,,</math> |
|||
:<math>F_{n+1}F_{m} + F_n F_{m-1} = F_{m+n}\,.</math> |
|||
In particular, with <math>m = n</math>, |
|||
:<math>F_{2n-1} = F_n^2 + F_{n-1}^2\,,</math> |
|||
:<math>F_{2n} = (F_{n-1}+F_{n+1})F_n = (2F_{n-1}+F_n)F_n\,.</math> |
|||
==Recognizing Fibonacci numbers== |
|||
The question may arise whether a positive integer ''z'' is a Fibonacci number. Since <math>F(n)</math> is the closest integer to <math>\varphi^n/\sqrt{5}</math>, the most straightforward, brute-force test is the identity |
|||
:<math>F\bigg(\bigg\lfloor\log_\varphi\bigg(z\cdot\sqrt{5}+\frac{1}{2}\bigg)\bigg\rfloor\bigg)=z,</math> |
|||
which is true [[if and only if]] ''z'' is a Fibonacci number. In this formula, <math>F(n)</math> can be computed rapidly using any of the previously discussed closed-form expressions. |
|||
One implication of the above expression is this: if it is known that a number ''z'' is a Fibonacci number, we may determine an ''n'' such that ''F(n) = z'' by the following: |
|||
:<math>\bigg\lfloor\log_\varphi\bigg(z\cdot\sqrt{5}+\frac{1}{2}\bigg)\bigg\rfloor = n</math> |
|||
Alternatively, a positive integer ''z'' is a Fibonacci number if and only if one of <math>5z^2+4</math> or <math>5z^2-4</math> is a [[Square number|perfect square]].<ref>{{Cite book|last=Posamentier |first=Alfred |coauthors = Lehmann, Ingmar |title=The (Fabulous) FIBONACCI Numbers |year=2007 |isbn=978-1-59102-475-0 |publisher=Prometheus Books |page=305}}</ref> |
|||
A slightly more sophisticated test uses the fact that the [[convergent (continued fraction)|convergent]]s of the [[continued fraction]] representation of <math>\varphi\, </math> are ratios of successive Fibonacci numbers. That is, the inequality |
|||
:<math>\bigg|\varphi-\frac{p}{q}\bigg|<\frac{1}{q^2}</math> |
|||
(with [[coprime]] positive integers ''p'', ''q'') is true if and only if ''p'' and ''q'' are successive Fibonacci numbers. From this one derives the criterion that ''z'' is a Fibonacci number if and only if the [[closed interval]] |
|||
:<math>\bigg[\varphi z-\frac{1}{z},\varphi z+\frac{1}{z}\bigg]</math> |
|||
contains a positive integer.<ref>M. Möbius, ''Wie erkennt man eine Fibonacci Zahl?'', Math. Semesterber. (1998) 45; 243–246.</ref> For <math>z \geq 2</math>, it is easy to show that this interval contains at most one integer, and in the event that ''z'' is a Fibonacci number, the contained integer is equal to the next successive Fibonacci number after ''z''. Somewhat remarkably, this result still holds for the case <math>z=1</math>, but it must be stated carefully since <math>1</math> appears twice in the Fibonacci sequence, and thus has two distinct successors. |
|||
==Identities== |
|||
Most identities involving Fibonacci numbers draw from [[combinatorial proof|combinatorial arguments]]. |
|||
''F''(''n'') can be interpreted as the number of sequences of 1s and 2s that sum to ''n'' − 1, with the convention that ''F''(0) = 0, meaning no sum will add up to −1, and that ''F''(1) = 1, meaning the empty sum will "add up" to 0. |
|||
Here the order of the summands matters. For example, 1 + 2 and 2 + 1 are considered two different sums and are counted twice. |
|||
===First identity=== |
|||
: <math>F_{n} = F_{n-1} + F_{n-2} \, </math> |
|||
:''For n > 1.'' |
|||
:''The nth Fibonacci number is the sum of the previous two Fibonacci numbers.'' |
|||
{| class="collapsible collapsed" style="width:100%; border:1px solid #aaa;" |
|||
|- |
|||
! style="background:#ccf;"|Proof |
|||
|- |
|||
| |
|||
We must establish that the sequence of numbers defined by the combinatorial interpretation above satisfy the same recurrence relation as the Fibonacci numbers (and so are indeed identical to the Fibonacci numbers). |
|||
The set of ''F''(''n'' + 1) ways of making ordered sums of 1s and 2s that sum to ''n'' may be divided into two non-overlapping sets. The first set contains those sums whose first summand is 1; the remainder sums to ''n'' − 1, so there are ''F''(''n'') sums in the first set. The second set contains those sums whose first summand is 2; the remainder sums to ''n'' − 2, so there are ''F''(''n'' − 1) sums in the second set. The first summand can only be 1 or 2, so these two sets exhaust the original set. Thus ''F''(''n'' + 1) = ''F''(''n'') + ''F''(''n'' − 1). |
|||
|} |
|||
===Second identity=== |
|||
The sum of the first ''n'' Fibonacci numbers is equal to the ''n''+2<sup>nd</sup> Fibonacci number minus 1.<ref>Lucas p. 4</ref> In symbols: |
|||
:<math>\sum_{i=0}^n F_i = F_{n+2} - 1</math> |
|||
:''The sum of the first ''n'' Fibonacci numbers is the (''n'' + 2)nd Fibonacci number minus 1.'' |
|||
{| class="collapsible collapsed" style="width:100%; border:1px solid #aaa;" |
|||
|- |
|||
! style="background:#ccf;"|Proof |
|||
|- |
|||
| |
|||
We count the number of ways summing 1s and 2s to ''n'' + 1 such that at least one of the summands is 2. |
|||
As before, there are ''F''(''n'' + 2) ways summing 1s and 2s to ''n'' + 1 when ''n'' ≥ 0. |
|||
Since there is only one sum of ''n'' + 1 that does not use any 2, namely 1 + ... + 1 (''n'' + 1 terms), we subtract 1 from ''F''(''n'' + 2). |
|||
Equivalently, we can consider the first occurrence of 2 as a summand. |
|||
If, in a sum, the first summand is 2, then there are ''F''(''n'') ways to the complete the counting for ''n'' − 1. |
|||
If the second summand is 2 but the first is 1, then there are ''F''(''n'' − 1) ways to complete the counting for ''n'' − 2. |
|||
Proceed in this fashion. |
|||
Eventually we consider the (''n'' + 1)th summand. |
|||
If it is 2 but all of the previous ''n'' summands are 1s, then there are ''F''(0) ways to complete the counting for 0. |
|||
If a sum contains 2 as a summand, the first occurrence of such summand must take place in between the first and (''n'' + 1)th position. |
|||
Thus ''F''(''n'') + ''F''(''n'' − 1) + ... + ''F''(0) gives the desired counting. |
|||
By induction: |
|||
:For <math>n=0</math>, <math>\sum_{i=0}^0 F_i = F_2 - 1 = 1 - 1 = 0</math>, so the equation is true for <math>n=0</math>. |
|||
:For <math>n=x</math>, assume <math>\sum_{i=0}^x F_i = F_{x+2} - 1</math>. |
|||
:Add the next Fibonacci number <math>F_{x+1}</math> to both sides: <math>F_{x+1} + \sum_{i=0}^x F_i = F_{x+1} + F_{x+2} - 1</math>. |
|||
:By the Fibonacci recurrence relation, <math>F_{x+1} + F_{x+2} = F_{x+3}</math>, so <math>\sum_{i=0}^{x+1} F_i = F_{x+3} - 1</math>, which is the <math>n=x+1</math> case, proving that where the equation is true for <math>n=x</math>, so is it for <math>n=x+1</math>. |
|||
|} |
|||
===Third identity=== |
|||
This identity has slightly different forms for ''F''<sub>''j''</sub>, depending on whether ''j'' is odd or even. |
|||
''The sum of the first n − 1 Fibonacci numbers, F<sub>j</sub>, such that j is odd, is the (2n)th Fibonacci number.'' |
|||
:<math>\sum_{i=0}^{n-1} F_{2i+1} = F_{2n}</math> |
|||
''The sum of the first n Fibonacci numbers, F<sub>j</sub>, such that j is even, is the (2n + 1)th Fibonacci number minus 1.'' |
|||
:<math>\sum_{i=0}^{n} F_{2i} = F_{2n+1}-1</math> |
|||
<ref>{{Cite book|title = Fibonacci Numbers |last = Vorobiev |first = Nikolaĭ Nikolaevich |coauthors = Mircea Martin |publisher = Birkhäuser |year = 2002 |isbn = 3-7643-6135-2 |chapter=Chapter 1 |pages = 5–6}}</ref> |
|||
{| class="collapsible collapsed" style="width:100%; border:1px solid #aaa;" |
|||
|- |
|||
! style="background:#ccf;"|Proofs |
|||
|- |
|||
| |
|||
'''1: j is odd''' |
|||
By induction for ''F''<sub>2''n''</sub>: |
|||
:<math>F_1+F_3+F_5+\cdots+F_{2n-3}+F_{2n-1}=F_{2n}\,</math> |
|||
:<math>F_1+F_3+F_5+\cdots+F_{2n-3}+F_{2n-1}+F_{2n+1}=F_{2n}+F_{2n+1}\,</math> |
|||
:<math>F_1+F_3+F_5+\cdots+F_{2n-3}+F_{2n-1}+F_{2n+1}=F_{2n+2}\,</math> |
|||
A basis case for this could be ''F''<sub>1</sub> = ''F''<sub>2</sub>. |
|||
'''2: j is even''' |
|||
By induction for ''F''<sub>2''n''+1</sub>: |
|||
:<math>F_0+F_2+F_4+\cdots+F_{2n-2}+F_{2n}=F_{2n+1}-1\,</math> |
|||
:<math>F_0+F_2+F_4+\cdots+F_{2n-2}+F_{2n}+F_{2n+2}=F_{2n+1}+F_{2n+2}-1\,</math> |
|||
:<math>F_0+F_2+F_4+\cdots+F_{2n-2}+F_{2n}+F_{2n+2}=F_{2n+3}-1\,</math> |
|||
A basis case for this could be ''F''<sub>0</sub> = ''F''<sub>1</sub> − 1. |
|||
|} |
|||
<br> |
|||
{| class="collapsible collapsed" style="width:100%; border:1px solid #aaa;" |
|||
|- |
|||
! style="background:#ccf;"|Alternative proof |
|||
|- |
|||
| |
|||
By using identity 1 we can construct a telescoping sum: |
|||
:<math>\sum_{i=0}^{n-1} F_{2i+1} = \sum_{i=0}^{n-1} [ F_{2(i+1)}-F_{2i} ] = F_{2n}-F_{0} = F_{2n}</math> |
|||
If the summands are the Fibonacci numbers with even index, the proof is very similar. |
|||
Summing both cases yields identity 2. |
|||
|} |
|||
===Fourth identity=== |
|||
:<math>\sum_{i=0}^n iF_i = nF_{n+2} - F_{n+3} + 2</math> |
|||
{| class="collapsible collapsed" style="width:100%; border:1px solid #aaa;" |
|||
|- |
|||
! style="background:#ccf;"|Proof |
|||
|- |
|||
| |
|||
This identity can be established in two stages. |
|||
First, we count the number of ways summing 1s and 2s to −1, 0, ..., or ''n'' + 1 such that at least one of the summands is 2. |
|||
By our second identity, there are ''F''(''n'' + 2) − 1 ways summing to ''n'' + 1; ''F''(''n'' + 1) − 1 ways summing to ''n''; ...; and, eventually, ''F''(2) − 1 way summing to 1. |
|||
As ''F''(1) − 1 = ''F''(0) = 0, we can add up all ''n'' + 1 sums and apply the second identity again to obtain |
|||
: [''F''(''n'' + 2) − 1] + [''F''(''n'' + 1) − 1] + ... + [''F''(2) − 1] |
|||
: = [''F''(''n'' + 2) − 1] + [''F''(''n'' + 1) − 1] + ... + [''F''(2) − 1] + [''F''(1) − 1] + ''F''(0) |
|||
: = ''F''(''n'' + 2) + [''F''(''n'' + 1) + ... + ''F''(1) + ''F''(0)] − (''n'' + 2) |
|||
: = ''F''(''n'' + 2) + [''F''(''n'' + 3) − 1] − (''n'' + 2) |
|||
: = ''F''(''n'' + 2) + ''F''(''n'' + 3) − (''n'' + 3). |
|||
On the other hand, we observe from the second identity that there are |
|||
* ''F''(0) + ''F''(1) + ... + ''F''(''n'' − 1) + ''F''(''n'') ways summing to ''n'' + 1; |
|||
* ''F''(0) + ''F''(1) + ... + ''F''(''n'' − 1) ways summing to ''n''; |
|||
...... |
|||
* ''F''(0) way summing to −1. |
|||
Adding up all ''n'' + 1 sums, we see that there are |
|||
* (''n'' + 1) ''F''(0) + ''n'' ''F''(1) + ... + ''F''(''n'') ways summing to −1, 0, ..., or ''n'' + 1. |
|||
Since the two methods of counting refer to the same number, we have |
|||
: (''n'' + 1) ''F''(0) + ''n'' ''F''(1) + ... + ''F''(''n'') = ''F''(''n'' + 2) + ''F''(''n'' + 3) − (''n'' + 3) |
|||
Finally, we complete the proof by subtracting the above identity from ''n'' + 1 times the second identity. |
|||
|} |
|||
===Fifth identity=== |
|||
:<math>\sum_{i=0}^n {F_i}^2 = F_{n} F_{n+1}</math> |
|||
:''The sum of the squares of the first n Fibonacci numbers is the product of the nth and (n + 1)th Fibonacci numbers.'' |
|||
{| class="collapsible collapsed" style="width:100%; border:1px solid #aaa;" |
|||
|- |
|||
! style="background:#ccf;"|Proof |
|||
|- |
|||
| |
|||
Although this identity can be established by either induction or direct, albeit messy, algebraic manipulation, perhaps the most elegant and most insightful method is by a simple geometric argument. |
|||
Consider the Fibonacci Rectangles constructed in previous sections. Using a common trick, we will compute the area of this rectangle in two different ways. But since this must yield the same answer in both cases, we know these resulting expressions must be equal, which will yield the desired identity. |
|||
On the one hand, the ''n''-th rectangle is composed of ''n'' squares, whose side lengths are ''F''(1), ''F''(2), ..., ''F''(''n''). Its area is therefore the sum of each of these squares, which is given by |
|||
:<math>\sum_{i=0}^n {F_i}^2.</math> |
|||
On the other hand, we know that the ''n''-th rectangle has side lengths ''F''(''n'') and ''F''(''n'' + 1). Thus, its area is simply given by |
|||
:<math>F_{n} F_{n+1}. \, </math> |
|||
Setting these expressions equal to each other completes the proof. |
|||
|} |
|||
===Identity for doubling ''n''=== |
|||
:<math>F_{2n} = F_{n+1}^2 - F_{n-1}^2 = F_n(F_{n+1}+F_{n-1}) = F_nL_n</math><ref name="MathWorld">{{MathWorld|urlname=FibonacciNumber |title=Fibonacci Number}}</ref> |
|||
Where <math>L_n</math> is the ''n'''th [[Lucas Numbers|Lucas Number]]. |
|||
===Another identity=== |
|||
Another identity useful for calculating ''F<sub>n</sub>'' for large values of ''n'' is<ref name="MathWorld" /> |
|||
:<math>F_{kn+c} = \sum_{i=0}^k {k\choose i} F_{c-i} F_n^i F_{n+1}^{k-i},</math> |
|||
from which other identities for specific values of k, n, and c can be derived below, including |
|||
:<math>F_{2n+k} = F_k F_{n+1}^2 + 2 F_{k-1} F_{n+1} F_n + F_{k-2} F_n^2 </math> |
|||
for all integers ''n'' and ''k''. Doubling identities of this type can be used to calculate ''F<sub>n</sub>'' using O(log ''n'') [[long multiplication]] operations of size ''n'' bits. The number of bits of precision needed to perform each multiplication doubles at each step, so the performance is limited by the final multiplication; if the fast [[Schönhage–Strassen algorithm|Schönhage–Strassen multiplication algorithm]] is used, this is O(''n'' log ''n'' log log ''n'') bit operations. Notice that, with the definition of Fibonacci numbers with negative ''n'' given in the introduction, this formula reduces to the ''double n'' formula when ''k'' = 0. |
|||
===Other identities=== |
|||
Other identities include relationships to the [[Lucas number]]s, which have the same recursive properties but start with ''L''<sub>0</sub> = 2 and ''L''<sub>1</sub> = 1. These properties include ''F''<sub>2''n''</sub> = ''F''<sub>''n''</sub>''L''<sub>''n''</sub>. |
|||
There are also scaling identities, which take you from ''F''<sub>''n''</sub> and ''F''<sub>''n''+1</sub> to a variety of things of the form ''F''<sub>''an''+''b''</sub>; for instance |
|||
: <math>F_{3n} = 2F_n^3 + 3F_n F_{n+1} F_{n-1} = 5F_n^3 + 3 (-1)^n F_n \, </math> by Cassini's identity. |
|||
: <math>F_{3n+1} = F_{n+1}^3 + 3 F_{n+1}F_n^2 - F_n^3 \, </math> |
|||
: <math>F_{3n+2} = F_{n+1}^3 + 3 F_{n+1}^2F_n + F_n^3 \, </math> |
|||
: <math>F_{4n} = 4F_nF_{n+1}(F_{n+1}^2 + 2F_n^2) - 3F_n^2(F_n^2 + 2F_{n+1}^2) \, </math> |
|||
These can be found experimentally using [[lattice reduction]], and are useful in setting up the [[special number field sieve]] to [[Factorization|factorize]] a Fibonacci number. Such relations exist in a very general sense for numbers defined by recurrence relations. See the section on multiplication formulae under [[Perrin number]]s for details. |
|||
==Power series== |
|||
The [[generating function]] of the Fibonacci sequence is the [[power series]] |
|||
:<math>s(x)=\sum_{k=0}^{\infty} F_k x^k.</math> |
|||
This series has a simple and interesting closed-form solution for <math>|x| < \frac{1}{\varphi}</math>:<ref>Glaister, P.. ''Fibonacci power series''. The Mathematical Gazette, 1995, p. 521.</ref> |
|||
:<math>s(x)=\frac{x}{1-x-x^2}.</math> |
|||
This solution can be proven by using the Fibonacci recurrence to expand each coefficient in the infinite sum defining <math>s(x)</math>: |
|||
:<math>\begin{align} |
|||
s(x) &= \sum_{k=0}^{\infty} F_k x^k \\ |
|||
&= F_0 + F_1x + \sum_{k=2}^{\infty} \left( F_{k-1} + F_{k-2} \right) x^k \\ |
|||
&= x + \sum_{k=2}^{\infty} F_{k-1} x^k + \sum_{k=2}^{\infty} F_{k-2} x^k \\ |
|||
&= x + x\sum_{k=0}^{\infty} F_k x^k + x^2\sum_{k=0}^{\infty} F_k x^k \\ |
|||
&= x + x s(x) + x^2 s(x). |
|||
\end{align}</math> |
|||
Solving the equation <math>s(x)=x+xs(x)+x^2s(x)</math> for <math>s(x)</math> results in the closed form solution. |
|||
In particular, math puzzle-books note the curious value <math>\frac{s(\frac{1}{10})}{10}=\frac{1}{89}</math>,<ref>[http://www.geom.uiuc.edu/~rminer/1over89/ The Remarkable Number 1/89] at The Geometry Center.</ref> or more generally |
|||
:<math>\sum_{n = 1}^{\infty}{\frac {F_n}{10^{(k + 1)(n + 1)}}} = \frac {1}{10^{2k + 2} - 10^{k + 1} - 1}</math> |
|||
for all integers <math>k \geq 0</math>. |
|||
Conversely, |
|||
:<math>\sum_{n=0}^\infty\,\frac{F_n}{k^{n}}\,=\,\frac{k}{k^{2}-k-1}.</math> |
|||
==Reciprocal sums== |
|||
<!-- |
|||
{{cite book |
|||
| last =Borwein |
|||
| first =Jonathan M. |
|||
| authorlink =Jonathan Borwein |
|||
| coauthors =[[Peter Borwein|Peter B. Borwein]] |
|||
| title =Pi and the AGM: A Study in Analytic Number Theory and Computational Complexity |
|||
| pages =91–101 |
|||
| publisher =Wiley |
|||
| year =1998 |
|||
| month =July |
|||
| url =http://www.wiley.com/WileyCDA/WileyTitle/productCd-047131515X.html |
|||
| isbn = 978-0-471-31515-5 }} |
|||
It credits some formulae to {{cite journal | author = Landau, E. | title = Sur la Série des Invers de Nombres de Fibonacci | journal = Bull. Soc. Math. France | volume = 27 | year = 1899 | pages = 298–300}} |
|||
--> |
|||
Infinite sums over reciprocal Fibonacci numbers can sometimes be evaluated in terms of [[theta function]]s. For example, we can write the sum of every odd-indexed reciprocal Fibonacci number as |
|||
:<math>\sum_{k=0}^\infty \frac{1}{F_{2k+1}} = \frac{\sqrt{5}}{4}\vartheta_2^2 \left(0, \frac{3-\sqrt 5}{2}\right) ,</math> |
|||
and the sum of squared reciprocal Fibonacci numbers as |
|||
:<math>\sum_{k=1}^\infty \frac{1}{F_k^2} = \frac{5}{24} \left(\vartheta_2^4\left(0, \frac{3-\sqrt 5}{2}\right) - \vartheta_4^4\left(0, \frac{3-\sqrt 5}{2}\right) + 1 \right).</math> |
|||
If we add 1 to each Fibonacci number in the first sum, there is also the closed form |
|||
:<math>\sum_{k=0}^\infty \frac{1}{1+F_{2k+1}} = \frac{\sqrt{5}}{2},</math> |
|||
and there is a nice ''nested'' sum of squared Fibonacci numbers giving the reciprocal of the [[golden ratio]], |
|||
:<math>\sum_{k=1}^\infty \frac{(-1)^{k+1}}{\sum_{j=1}^k {F_{j}}^2} = \frac{\sqrt{5}-1}{2}.</math> |
|||
Results such as these make it plausible that a closed formula for the plain sum of reciprocal Fibonacci numbers could be found, but none is yet known. Despite that, the [[reciprocal Fibonacci constant]] |
|||
:<math>\psi = \sum_{k=1}^{\infty} \frac{1}{F_k} = 3.359885666243 \dots</math> |
|||
has been proved [[irrational number|irrational]] by [[Richard André-Jeannin]]. |
|||
'''Millin series''' gives a remarkable identity:<ref>{{MathWorld |title=Millin Series |urlname=MillinSeries}}</ref> |
|||
:<math>\sum_{n=0}^{\infty} \frac{1}{F_{2^n}} = \frac{7 - \sqrt{5}}{2}</math> |
|||
which follows from the closed form for its partial sums as ''N'' tends to infinity: |
|||
:<math>\sum_{n=0}^N \frac{1}{F_{2^n}} = 3 - \frac{F_{2^N-1}}{F_{2^N}}.</math> |
|||
==Primes and divisibility== |
|||
===Divisibility properties=== |
|||
Every 3rd number of the sequence is even and more generally, every ''k''th number of the sequence is a multiple of ''F<sub>k</sub>''. Thus the Fibonacci sequence is an example of a [[divisibility sequence]]. In fact, the Fibonacci sequence satisfies the stronger divisibility property |
|||
:<math>\gcd(F_m,F_n) = F_{\gcd(m,n)}\, .</math> |
|||
===Fibonacci primes=== |
|||
{{Main|Fibonacci prime}} |
|||
A '''Fibonacci prime''' is a Fibonacci number that is [[prime number|prime]] {{OEIS|id=A005478}}. The first few are: |
|||
: 2, 3, 5, 13, 89, 233, 1597, 28657, 514229, ... |
|||
Fibonacci primes with thousands of digits have been found, but it is not known whether there are infinitely many.<ref>{{MathWorld |urlname=FibonacciPrime |title=Fibonacci Prime }}</ref> |
|||
''F''<sub>''kn''</sub> is divisible by ''F''<sub>''n''</sub>, so, apart from ''F''<sub>4</sub> = 3, any Fibonacci prime must have a prime index. As there are [[Arbitrarily large|arbitrarily long]] runs of [[composite number]]s, there are therefore also arbitrarily long runs of composite Fibonacci numbers. |
|||
With the exceptions of 1, 8 and 144 (''F''<sub>1</sub> = ''F''<sub>2</sub>, ''F''<sub>6</sub> and ''F''<sub>12</sub>) every Fibonacci number has a prime factor that is not a factor of any smaller Fibonacci number ([[Carmichael's theorem]]).<ref>Ron Knott, [http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibtable.html "The Fibonacci numbers"].</ref> |
|||
144 is the only nontrivial |
|||
[[square number|square]] Fibonacci number.<ref>{{Cite journal|title=Square Fibonacci Numbers Etc |author= J H E Cohn |journal= Fibonacci Quarterly |volume= 2 |year= 1964 |pages=109–113 |url= http://math.la.asu.edu/~checkman/SquareFibonacci.html}}</ref> Attila Pethő proved<ref>A. Pethő, Diophantine properties of linear recursive sequences II, ''Acta Math. Paedagogicae Nyíregyháziensis'', '''17'''(2001), 81–96.</ref> in 2001 that there are only finitely many perfect power Fibonacci numbers. In 2006, Y. Bugeaud, M. Mignotte, and S. Siksek proved that only 8 and 144 are non-trivial perfect powers.<ref>Y. Bugeaud, M. Mignotte, S. Siksek: Classical and modular approaches to exponential Diophantine equations. I. Fibonacci and Lucas perfect powers. |
|||
''Ann. Math.'' (2), '''163'''(2006), 969–1018.</ref> |
|||
No Fibonacci number greater than ''F''<sub>6</sub> = 8 is one greater or one less than a prime number.<ref>Ross Honsberger ''Mathematical Gems III'' (AMS Dolciani Mathematical Expositions No. 9), 1985, ISBN 0-88385-318-3, p. 133.</ref> |
|||
Any three consecutive Fibonacci numbers, taken two at a time, are [[relatively prime]]: that is, |
|||
:[[greatest common divisor|gcd]](''F''<sub>''n''</sub>, ''F''<sub>''n''+1</sub>) = gcd(''F''<sub>''n''</sub>, ''F''<sub>''n''+2</sub>) = 1. |
|||
More generally, |
|||
:gcd(''F''<sub>''n''</sub>, ''F''<sub>''m''</sub>) = ''F''<sub>gcd(''n'', ''m'').</sub><ref>[[Paulo Ribenboim]], ''My Numbers, My Friends'', Springer-Verlag 2000.</ref><ref>Su, Francis E., et al. [http://www.math.hmc.edu/funfacts/ffiles/20004.5.shtml "Fibonacci GCD's, please."], ''Mudd Math Fun Facts''.</ref> |
|||
===Prime divisors of Fibonacci numbers=== |
|||
The divisibility of Fibonacci numbers by a prime ''p'' is related to the [[Legendre symbol]] <math>\;\left(\tfrac{p}{5}\right)</math> which is evaluated as follows: |
|||
:<math>\left(\frac{p}{5}\right) = \begin{cases} 0 & \textrm{if}\;p =5\\ 1 &\textrm{if}\;p \equiv \pm1 \pmod 5\\ -1 &\textrm{if}\;p \equiv \pm2 \pmod 5.\end{cases}</math> |
|||
If ''p'' is a prime number then |
|||
<math> |
|||
F_p \equiv \left(\frac{p}{5}\right) \pmod p \;\;\text{ and }\;\;\; |
|||
F_{p-\left(\frac{p}{5}\right)} \equiv 0 \pmod p. |
|||
</math><ref>[[Paulo Ribenboim]] (1996), ''The New Book of Prime Number Records'', New York: Springer, ISBN 0-387-94457-5, p. 64.</ref><ref>Franz Lemmermeyer (2000), ''Reciprocity Laws'', New York: Springer, ISBN 3-540-66957-4, ex 2.25–2.28, pp. 73–74.</ref> |
|||
<blockquote> |
|||
For example, |
|||
:<math>\begin{align} |
|||
(\tfrac{2}{5}) &= -1, & F_3 &= 2, &F_2&=1, \\ |
|||
(\tfrac{3}{5}) &= -1, &F_4 &= 3,&F_3&=2, \\ |
|||
(\tfrac{5}{5}) &= 0, &F_5 &= 5, \\ |
|||
(\tfrac{7}{5}) &= -1, &F_8 &= 21,&F_7&=13, \\ |
|||
(\tfrac{11}{5})& = +1, & F_{10}& = 55, &F_{11}&=89. |
|||
\end{align} |
|||
</math> |
|||
</blockquote> |
|||
It is not known whether there exists a prime ''p'' such that <math>F_{p-\left(\frac{p}{5}\right)} \equiv 0 \pmod{p^2}</math>. Such primes (if there are any) would be called [[Wall–Sun–Sun prime]]s. |
|||
Also, if ''p'' ≠ 5 is an odd prime number then:<ref>Lemmermeyer, ex. 2.28, pp. 73–74.</ref> |
|||
:<math>5F^2_{\left(p \pm 1 \right) / 2} |
|||
\equiv |
|||
\begin{cases} |
|||
\frac{5\left(\frac{p}{5}\right)\pm 5}{2} \pmod p & \textrm{if}\;p \equiv 1 \pmod 4\\ |
|||
\\ |
|||
\frac{5\left(\frac{p}{5}\right)\mp 3}{2} \pmod p & \textrm{if}\;p \equiv 3 \pmod 4. |
|||
\end{cases} |
|||
</math> |
|||
<blockquote> |
|||
Examples of all the cases: |
|||
:<math>p=7 \equiv 3 \pmod 4, \;\;(\tfrac{7}{5}) = -1, \frac{5(\frac{7}{5})+3}{2} =-1\text{ and }\frac{5(\frac{7}{5})-3}{2}=-4.</math> |
|||
::<math>F_3=2 \text{ and } F_4=3.\ </math> |
|||
::<math>5F_3^2=20\equiv -1 \pmod {7}\;\;\text{ and }\;\;5F_4^2=45\equiv -4 \pmod {7}</math> |
|||
:<math>p=11 \equiv 3 \pmod 4, \;\;(\tfrac{11}{5}) = +1, \frac{5(\frac{11}{5})+3}{2} =4\text{ and }\frac{5(\frac{11}{5})- 3}{2}=1.</math> |
|||
::<math>F_5=5 \text{ and } F_6=8.\ </math> |
|||
::<math>5F_5^2=125\equiv 4 \pmod {11} \;\;\text{ and }\;\;5F_6^2=320\equiv 1 \pmod {11}</math> |
|||
:<math>p=13 \equiv 1 \pmod 4, \;\;(\tfrac{13}{5}) = -1, \frac{5(\frac{13}{5})-5}{2} =-5\text{ and }\frac{5(\frac{13}{5})+ 5}{2}=0.</math> |
|||
::<math>F_6=8 \text{ and } F_7=13.\ </math> |
|||
::<math>5F_6^2=320\equiv -5 \pmod {13} \;\;\text{ and }\;\;5F_7^2=845\equiv 0 \pmod {13}</math> |
|||
:<math>p=29 \equiv 1 \pmod 4, \;\;(\tfrac{29}{5}) = +1, \frac{5(\frac{29}{5})-5}{2} =0\text{ and }\frac{5(\frac{29}{5})+5}{2}=5.\ </math> |
|||
::<math>F_{14}=377 \text{ and } F_{15}=610.\ </math> |
|||
::<math>5F_{14}^2=710645\equiv 0 \pmod {29} \;\;\text{ and }\;\;5F_{15}^2=1860500\equiv 5 \pmod {29}</math> |
|||
</blockquote> |
|||
For odd ''n'', all odd prime divisors of ''F''<sub>''n''</sub> are ≡ 1 (mod 4), implying that all odd divisors of ''F''<sub>''n''</sub> (as the products of odd prime divisors) are ≡ 1 (mod 4).<ref>Lemmermeyer, ex. 2.27 p. 73.</ref><ref>The website [http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibtable.html] has the first 300 Fibonacci numbers factored into primes.</ref> |
|||
<blockquote>For example, |
|||
''F''<sub>1</sub> = 1, ''F''<sub>3</sub> = 2, ''F''<sub>5</sub> = 5, ''F''<sub>7</sub> = 13, ''F''<sub>9</sub> = 34 = 2×17, ''F''<sub>11</sub> = 89, ''F''<sub>13</sub> = 233, ''F''<sub>15</sub> = 610 = 2×5×61 |
|||
</blockquote> |
|||
===Periodicity modulo ''n''=== |
|||
{{Main|Pisano period}} |
|||
It may be seen that if the members of the Fibonacci sequence are taken mod ''n'', the resulting sequence must be [[periodic sequence|periodic]] with period at most ''n''<sup>2</sup>. The lengths of the periods for various ''n'' form the so-called [[Pisano period]]s {{OEIS|id=A001175}}. Determining the Pisano periods in general is an open problem,{{Citation needed|date=March 2008}} although for any particular ''n'' it can be solved as an instance of [[cycle detection]]. |
|||
==Right triangles== |
|||
Starting with 5, every second Fibonacci number is the length of the hypotenuse of a right triangle with integer sides, or in other words, the largest number in a [[Pythagorean triple]]. The length of the longer leg of this triangle is equal to the sum of the three sides of the preceding triangle in this series of triangles, and the shorter leg is equal to the difference between the preceding bypassed Fibonacci number and the shorter leg of the preceding triangle. |
|||
The first triangle in this series has sides of length 5, 4, and 3. Skipping 8, the next triangle has sides of length 13, 12 (5 + 4 + 3), and 5 (8 − 3). Skipping 21, the next triangle has sides of length 34, 30 (13 + 12 + 5), and 16 (21 − 5). This series continues indefinitely. The triangle sides ''a'', ''b'', ''c'' can be calculated directly: |
|||
:<math>\displaystyle a_n = F_{2n-1}</math> |
|||
:<math>\displaystyle b_n = 2 F_n F_{n-1}</math> |
|||
:<math>\displaystyle c_n = F_n^2 - F_{n-1}^2.</math> |
|||
These formulas satisfy <math>a_n ^2 = b_n ^2 + c_n ^2</math> for all ''n'', but they only represent triangle sides when ''n'' > 2. |
|||
Any four consecutive Fibonacci numbers ''F''<sub>''n''</sub>, ''F''<sub>''n''+1</sub>, ''F''<sub>''n''+2</sub> and ''F''<sub>''n''+3</sub> can also be used to generate a Pythagorean triple in a different way<ref>{{cite book |title=Elementary number theory with applications |first=Thomas|last=Koshy|publisher=Academic Press|year=2007 |
|||
|isbn=0123724872|page=581}}</ref>: |
|||
:<math> a = F_n F_{n+3} \, ; \, b = 2 F_{n+1} F_{n+2} \, ; \, c = F_{n+1}^2 + F_{n+2}^2 \, ; \, a^2 + b^2 = c^2 \,.</math> |
|||
Example 1: let the Fibonacci numbers be 1, 2, 3 and 5. Then: |
|||
:<math>\displaystyle a = 1 \times 5 = 5</math> |
|||
:<math>\displaystyle b = 2 \times 2 \times 3 = 12</math> |
|||
:<math>\displaystyle c = 2^2 + 3^2 = 13 \,</math> |
|||
:<math>\displaystyle 5^2 + 12^2 = 13^2 \,.</math> |
|||
==Magnitude== |
|||
Since <math>F_n</math> is [[Asymptotic analysis|asymptotic]] to <math>\varphi^n/\sqrt5</math>, the number of digits in <math>F_n\,</math> is asymptotic to <math>n\,\log_{10}\varphi\approx0.2090\,n</math>. As a consequence, for every integer <math>d>1</math> there are either 4 or 5 Fibonacci numbers with ''d'' decimal digits. |
|||
More generally, in the base ''b'' representation, the number of digits in <math>F_n</math> is asymptotic to <math>n\,\log_b\varphi</math>. |
|||
==Applications== |
|||
The Fibonacci numbers are important in the computational run-time analysis of [[Euclidean algorithm|Euclid's algorithm]] to determine the [[greatest common divisor]] of two integers: the worst case input for this algorithm is a pair of consecutive Fibonacci numbers.<ref>{{Cite book|first=Donald E.|last=Knuth|authorlink=Donald Knuth|year=1997|title=The Art of Computer Programming, Volume 1: Fundamental Algorithms|edition=3rd|publisher=Addison–Wesley|isbn=0-201-89683-4}} (p. 343).</ref> |
|||
[[Yuri Matiyasevich]] was able to show that the Fibonacci numbers can be defined by a [[Diophantine equation]], which led to [[Matiyasevich's theorem|his original solution]] of [[Hilbert's tenth problem]]. |
|||
The Fibonacci numbers are also an example of a [[complete sequence]]. This means that every positive integer can be written as a sum of Fibonacci numbers, where any one number is used once at most. Specifically, every positive integer can be written in a unique way as the sum of ''one or more'' distinct Fibonacci numbers in such a way that the sum does not include any two consecutive Fibonacci numbers. This is known as [[Zeckendorf's theorem]], and a sum of Fibonacci numbers that satisfies these conditions is called a Zeckendorf representation. The Zeckendorf representation of a number can be used to derive its [[Fibonacci coding]]. |
|||
Fibonacci numbers are used by some [[pseudorandom number generators]].<!-- Knuth vol. 2 --> |
|||
Fibonacci numbers are used in a polyphase version of the [[merge sort]] algorithm in which an unsorted list is divided into two lists whose lengths correspond to sequential Fibonacci numbers – by dividing the list so that the two parts have lengths in the approximate proportion φ. A tape-drive implementation of the [[polyphase merge sort]] was described in ''[[The Art of Computer Programming]]''. |
|||
Fibonacci numbers arise in the analysis of the [[Fibonacci heap]] data structure. |
|||
The [[Fibonacci cube]] is an [[undirected graph]] with a Fibonacci number of nodes that has been proposed as a [[network topology]] for [[parallel computing]]. |
|||
A one-dimensional optimization method, called the [[Fibonacci search technique]], uses Fibonacci numbers.<ref>{{Cite journal|author=M. Avriel and D.J. Wilde |title=Optimality of the Symmetric Fibonacci Search Technique |journal=Fibonacci Quarterly|year=1966 |issue=3 |pages= 265–269}}</ref> |
|||
The Fibonacci number series is used for optional [[lossy compression]] in the [[Interchange File Format|IFF]] [[8SVX]] audio file format used on [[Amiga]] computers. The number series [[companding|compands]] the original audio wave similar to logarithmic methods such as [[µ-law]].<ref>Amiga ROM Kernel Reference Manual, Addison–Wesley 1991.</ref><ref>[http://wiki.multimedia.cx/index.php?title=IFF#Fibonacci_Delta_Compression IFF – MultimediaWiki].</ref> |
|||
In [[music]], Fibonacci numbers are sometimes used to determine tunings, and, as in visual art, to determine the length or size of content or [[form (music)|formal]] elements. It is commonly thought that the third movement of [[Béla Bartók]]'s ''[[Music for Strings, Percussion, and Celesta]]'' was structured using Fibonacci numbers. |
|||
Since the [[conversion of units|conversion]] factor 1.609344 for miles to kilometers is close to the golden ratio (denoted φ), the decomposition of distance in miles into a sum of Fibonacci numbers becomes nearly the kilometer sum when the Fibonacci numbers are replaced by their successors. This method amounts to a [[radix]] 2 number [[processor register|register]] in [[golden ratio base]] φ being shifted. To convert from kilometers to miles, shift the register down the Fibonacci sequence instead.<ref>[http://eom.springer.de/Z/z120020.htm Zeckendorf representation].</ref> |
|||
==In nature== |
|||
[[File:FibonacciChamomile.PNG|frame|size 300px|[[Yellow Chamomile]] head showing the arrangement in 21 (blue) and 13 (aqua) spirals. Such arrangements involving consecutive Fibonacci numbers appear in a wide variety of plants.]] |
|||
Fibonacci sequences appear in biological settings,<ref name="S. Douady and Y. Couder 1996 255–274"/> in two consecutive Fibonacci numbers, such as branching in trees, [[Phyllotaxis|arrangement of leaves on a stem]], the fruitlets of a [[pineapple]],<ref name="Jones 2006 544"/> the flowering of [[artichoke]], an uncurling fern and the arrangement of a [[pine cone]].<ref name="A. Brousseau 1969 525–532"/> In addition, numerous poorly substantiated claims of Fibonacci numbers or [[golden section]]s in nature are found in popular sources, e.g., relating to the breeding of rabbits, the spirals of shells, and the curve of waves.<ref>{{cite web|url=http://www.lhup.edu/~dsimanek/pseudo/fibonacc.htm |title=Fibonacci Flim-Flam}}</ref> The Fibonacci numbers are also found in the family tree of honeybees.<ref>{{cite web|url = http://www.cs4fn.org/maths/bee-davinci.php |work = Computer Science For Fun: CS4FN |title = Marks for the da Vinci Code: B– }}</ref> |
|||
[[Przemysław Prusinkiewicz]] advanced the idea that real instances can in part be understood as the expression of certain algebraic constraints on [[free group]]s, specifically as certain [[L-system|Lindenmayer grammar]]s.<ref>{{Cite book|first=Przemyslaw |last=Prusinkiewicz |coauthors=James Hanan|title=Lindenmayer Systems, Fractals, and Plants (Lecture Notes in Biomathematics) |publisher=[[Springer Science+Business Media|Springer-Verlag]] |year=1989 |isbn=0-387-97092-4}}</ref> |
|||
[[Image:SunflowerModel.svg|thumb|left|Illustration of Vogel's model for ''n''=1 ... 500]] |
|||
A model for the pattern of [[floret]]s in the head of a [[sunflower]] was proposed by H. Vogel in 1979.<ref> |
|||
{{Cite journal |
|||
| last =Vogel |
|||
| first =H |
|||
| title =A better way to construct the sunflower head |
|||
| journal =Mathematical Biosciences |
|||
| issue =44 |
|||
| pages =179–189 |
|||
| year =1979 |
|||
| doi =10.1016/0025-5564(79)90080-4 |
|||
| volume =44 |
|||
| postscript =<!--None--> |
|||
}}</ref> |
|||
This has the form |
|||
:<math>\theta = \frac{2\pi}{\phi^2} n,\ r = c \sqrt{n}</math> |
|||
where ''n'' is the index number of the floret and ''c'' is a constant scaling factor; the florets thus lie on [[Fermat's spiral]]. The divergence angle, approximately 137.51°, is the [[golden angle]], dividing the circle in the golden ratio. Because this ratio is irrational, no floret has a neighbor at exactly the same angle from the center, so the florets pack efficiently. Because the rational approximations to the golden ratio are of the form ''F''(''j''):''F''(''j'' + 1), the nearest neighbors of floret number ''n'' are those at ''n'' ± ''F''(''j'') for some index ''j'' which depends on ''r'', the distance from the center. It is often said that sunflowers and similar arrangements have 55 spirals in one direction and 89 in the other (or some other pair of adjacent Fibonacci numbers), but this is true only of one range of radii, typically the outermost and thus most conspicuous.<ref>{{Cite book |
|||
| last =Prusinkiewicz |
|||
| first =Przemyslaw |
|||
| authorlink =Przemyslaw Prusinkiewicz |
|||
| coauthors =[[Aristid Lindenmayer|Lindenmayer, Aristid]] |
|||
| title =[[The Algorithmic Beauty of Plants]] |
|||
| publisher =Springer-Verlag |
|||
| year= 1990 |
|||
| location = |
|||
| pages =101–107 |
|||
| url =http://algorithmicbotany.org/papers/#webdocs |
|||
| doi = |
|||
| isbn = 978-0387972978 }}</ref> |
|||
===The bee ancestry code=== |
|||
Fibonacci numbers also appear in the description of the reproduction of a population of idealized honeybees, according to the following rules: |
|||
*If an egg is laid by an unmated female, it hatches a male or [[Drone (bee)|drone bee]]. |
|||
*If, however, an egg was fertilized by a male, it hatches a female. |
|||
Thus, a male bee will always have one parent, and a female bee will have two. |
|||
If one traces the ancestry of any male bee (1 bee), he has 1 parent (1 bee), 2 grandparents, 3 great-grandparents, 5 great-great-grandparents, and so on. This sequence of numbers of parents is the Fibonacci sequence. The number of ancestors at each level, ''F''<sub>''n''</sub>, is the number of female ancestors, which is ''F''<sub>''n''−1</sub>, plus the number of male ancestors, which is ''F''<sub>''n''−2</sub>.<ref>[http://www1.math.american.edu/newstudents/shared/puzzles/fibbee.html The Fibonacci Numbers and the Ancestry of Bees].</ref> (This is under the unrealistic assumption that the ancestors at each level are otherwise unrelated.) |
|||
==Popular culture== |
|||
{{Main|Fibonacci numbers in popular culture}} |
|||
<!--NOTE: YOUR FAVOURITE FIBONACCI REFERENCE SHOULD ONLY BE IN MAIN ARTICLE (Fibonacci numbers in popular culture) AND MAY ALREADY BE THERE!--> |
|||
==Generalizations== |
|||
{{Main|Generalizations of Fibonacci numbers}} |
|||
The Fibonacci sequence has been generalized in many ways. These include: |
|||
* Generalizing the index to negative integers to produce the [[Negafibonacci]] numbers. |
|||
* Generalizing the index to real numbers using a modification of Binet's formula.<ref name="MathWorld" /> |
|||
* Starting with other integers. [[Lucas number]]s have ''L''<sub>1</sub> = 1, ''L''<sub>2</sub> = 3, and ''L<sub>n</sub>'' = ''L''<sub>''n''−1</sub> + ''L''<sub>''n''−2</sub>. [[Primefree sequence]]s use the Fibonacci recursion with other starting points in order to generate sequences in which all numbers are [[composite number|composite]]. |
|||
* Letting a number be a linear function (other than the sum) of the 2 preceding numbers. The [[Pell number]]s have ''P<sub>n</sub>'' = 2''P''<sub>''n'' – 1</sub> + ''P''<sub>''n'' – 2</sub>. |
|||
* Not adding the immediately preceding numbers. The [[Padovan sequence]] and [[Perrin number]]s have ''P''(''n'') = ''P''(''n'' – 2) + ''P''(''n'' – 3). |
|||
* Generating the next number by adding 3 numbers (tribonacci numbers), 4 numbers (tetranacci numbers), or more. The resulting sequences are known as ''n-Step Fibonacci numbers''.<ref>{{MathWorld|urlname=Fibonaccin-StepNumber |title=Fibonacci ''n''-Step Number}}</ref> |
|||
* Adding other objects than integers, for example functions or strings—one essential example is [[Fibonacci polynomials]]. |
|||
==See also== |
|||
{{Refbegin|2}} |
|||
*[[Collatz conjecture]] |
|||
*[[Fibonacci word]] |
|||
*[[Helicoid]] |
|||
*[[Lucas numbers]] |
|||
*[[The Fibonacci Association]] |
|||
*[[Recursion (computer science)#Fibonacci]] |
|||
{{Refend}} |
|||
==Notes== |
|||
{{Reflist|colwidth=30em}} |
|||
{{inconsistent citations}} |
|||
==References== |
|||
*{{cite book|title=Strange Curves, Counting Rabbits, and Other Mathematical Explorations|first=Keith M.|last=Ball |
|||
|publisher=Princeton University Press|year=2003 |
|||
|chapter=Chapter 8: Fibonacci's Rabbits Revisited |
|||
|isbn=0691113211}} |
|||
*{{cite book |title=Théorie des nombres|first=Édouard|last=Lucas|publisher=Gauthier-Villars|year=1891|volume=1}} |
|||
==External links== |
|||
{{wikibooks|Fibonacci number program}} |
|||
<!--======================== {{No more links}} ============================ |
|||
| PLEASE BE CAUTIOUS IN ADDING MORE LINKS TO THIS ARTICLE. Wikipedia | |
|||
| is not a collection of links nor should it be used for advertising. | |
|||
| | |
|||
| Excessive or inappropriate links WILL BE DELETED. | |
|||
| See [[Wikipedia:External links]] & [[Wikipedia:Spam]] for details. | |
|||
| | |
|||
| If there are already plentiful links, please propose additions or | |
|||
| replacements on this article's discussion page, or submit your link | |
|||
| to the relevant category at the Open Directory Project (dmoz.org) | |
|||
| and link back to that category using the {{dmoz}} template. | |
|||
======================= {{No more links}} =====================--> |
|||
* {{In Our Time|Fibonacci Sequence|b008ct2j|Fibonacci_Sequence}} |
|||
* Sequence {{OEIS2C|A000045}} ''Fibonacci Numbers'' at the [[On-Line Encyclopedia of Integer Sequences]] |
|||
* [http://www.mathpages.com/home/kmath078.htm Periods of Fibonacci Sequences Mod m] at MathPages |
|||
* [http://www.physorg.com/news97227410.html Scientists find clues to the formation of Fibonacci spirals in nature] |
|||
* [http://wikinternet.com/wordpress/code/lisp/fibonacci-number/ Implementation to calculate Fibonacci sequence in Lisp] |
|||
{{DEFAULTSORT:Fibonacci Number}} |
|||
[[Category:Fibonacci numbers|*]] |
|||
[[Category:Articles containing proofs]] |
|||
[[ar:متتالية فيبوناتشي]] |
|||
[[az:Fibonaççi ədədləri]] |
|||
[[bn:ফিবোনাচ্চি রাশিমালা]] |
|||
[[bs:Fibonaccijev broj]] |
|||
[[bg:Числа на Фибоначи]] |
|||
[[ca:Successió de Fibonacci]] |
|||
[[cs:Fibonacciho posloupnost]] |
|||
[[da:Fibonacci-tal]] |
|||
[[de:Fibonacci-Folge]] |
|||
[[et:Fibonacci jada]] |
|||
[[el:Ακολουθία Φιμπονάτσι]] |
|||
[[es:Sucesión de Fibonacci]] |
|||
[[eo:Fibonaĉi-nombro]] |
|||
[[eu:Fibonacciren zenbakiak]] |
|||
[[fa:اعداد فیبوناچی]] |
|||
[[fr:Suite de Fibonacci]] |
|||
[[ga:Seicheamh Fibonacci]] |
|||
[[gv:Straih Fibonacci]] |
|||
[[ko:피보나치 수]] |
|||
[[hi:हेमचन्द्र श्रेणी]] |
|||
[[hr:Fibonaccijev broj]] |
|||
[[id:Bilangan Fibonacci]] |
|||
[[is:Fibonacci-runa]] |
|||
[[it:Successione di Fibonacci]] |
|||
[[he:סדרת פיבונאצ'י]] |
|||
[[kk:Фибоначчи сандары]] |
|||
[[la:Numeri Fibonacciani]] |
|||
[[lv:Fibonači skaitļi]] |
|||
[[lt:Fibonačio skaičius]] |
|||
[[hu:Fibonacci-számok]] |
|||
[[ml:ഫിബനാച്ചി ശ്രേണി]] |
|||
[[ms:Bilangan Fibonacci]] |
|||
[[mn:Фибоначчийн тоо]] |
|||
[[nl:Rij van Fibonacci]] |
|||
[[ja:フィボナッチ数]] |
|||
[[no:Fibonaccitall]] |
|||
[[nn:Fibonaccifølgja]] |
|||
[[uz:Fibonachchi sonlari]] |
|||
[[pms:Sequensa ëd Fibonacci]] |
|||
[[pl:Ciąg Fibonacciego]] |
|||
[[pt:Número de Fibonacci]] |
|||
[[kaa:Fibonachchi sanları]] |
|||
[[ro:Numerele Fibonacci]] |
|||
[[ru:Числа Фибоначчи]] |
|||
[[sq:Numrat e Fibonaccit]] |
|||
[[scn:Succissioni di Fibonacci]] |
|||
[[si:ෆිබොනාච්චි සංඛ්යා]] |
|||
[[simple:Fibonacci number]] |
|||
[[sk:Fibonacciho postupnosť]] |
|||
[[sl:Fibonaccijevo število]] |
|||
[[sr:Фибоначијев низ]] |
|||
[[fi:Fibonaccin lukujono]] |
|||
[[sv:Fibonaccital]] |
|||
[[ta:ஃபிபனாச்சி எண்கள்]] |
|||
[[th:เลขฟีโบนัชชี]] |
|||
[[tr:Fibonacci dizisi]] |
|||
[[uk:Послідовність Фібоначчі]] |
|||
[[vi:Dãy Fibonacci]] |
|||
[[vls:Reke van Fibonacci]] |
|||
[[zh:斐波那契数列]] |
|||
Revision as of 08:20, 2 September 2011

In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:
By definition, the first two Fibonacci numbers are 0 and 1, and each subsequent number is the sum of the previous two.
In mathematical terms, the sequence Fn of Fibonacci numbers is defined by the recurrence relation
with seed values
The Fibonacci sequence is named after Leonardo of Pisa, who was known as Fibonacci. Fibonacci's 1202 book Liber Abaci introduced the sequence to Western European mathematics,[2] although the sequence had been described earlier in Indian mathematics.[3][4][5] (By modern convention, the sequence begins with F0 = 0. The Liber Abaci began the sequence with F1 = 1, omitting the initial 0, and the sequence is still written this way by some.)
Fibonacci numbers are closely related to Lucas numbers in that they are a complementary pair of Lucas sequences. They are intimately connected with the golden ratio, for example the closest rational approximations to the ratio are 2/1, 3/2, 5/3, 8/5, ... . Applications include computer algorithms such as the Fibonacci search technique and the Fibonacci heap data structure, and graphs called Fibonacci cubes used for interconnecting parallel and distributed systems. They also appear in biological settings,[6] such as branching in trees, arrangement of leaves on a stem, the fruit spouts of a pineapple,[7] the flowering of artichoke, an uncurling fern and the arrangement of a pine cone.[8]
Origins
The Fibonacci sequence appears in Indian mathematics, in connection with Sanskrit prosody.[4][9] In the Sanskrit oral tradition, there was much emphasis on how long (L) syllables mix with the short (S), and counting the different patterns of L and S within a given fixed length results in the Fibonacci numbers; the number of patterns that are m short syllables long is the Fibonacci number Fm + 1.[5]
Susantha Goonatilake writes that the development of the Fibonacci sequence "is attributed in part to Pingala (200 BC), later being associated with Virahanka (c. 700 AD), Gopāla (c.1135 AD), and Hemachandra (c.1150)".[3] Parmanand Singh cites Pingala's cryptic formula misrau cha ("the two are mixed") and cites scholars who interpret it in context as saying that the cases for m beats (Fm) is obtained by adding a [S] to Fm−1 cases and [L] to the Fm−2 cases. He dates Pingala before 450 BCE.[10]
However, the clearest exposition of the series arises in the work of Virahanka (c. 700AD), whose own work is lost, but is available in a quotation by Gopala (c.1135):
- Variations of two earlier meters [is the variation]... For example, for [a meter of length] four, variations of meters of two [and] three being mixed, five happens. [works out examples 8, 13, 21]... In this way, the process should be followed in all mAtrA-vr.ttas (prosodic combinations).[11]
The series is also discussed by Gopala (before 1135AD) and by the Jain scholar Hemachandra (c. 1150AD).
In the West, the Fibonacci sequence first appears in the book Liber Abaci (1202) by Leonardo of Pisa, known as Fibonacci.[2] Fibonacci considers the growth of an idealized (biologically unrealistic) rabbit population, assuming that: a newly born pair of rabbits, one male, one female, are put in a field; rabbits are able to mate at the age of one month so that at the end of its second month a female can produce another pair of rabbits; rabbits never die and a mating pair always produces one new pair (one male, one female) every month from the second month on. The puzzle that Fibonacci posed was: how many pairs will there be in one year?
- At the end of the first month, they mate, but there is still only 1 pair.
- At the end of the second month the female produces a new pair, so now there are 2 pairs of rabbits in the field.
- At the end of the third month, the original female produces a second pair, making 3 pairs in all in the field.
- At the end of the fourth month, the original female has produced yet another new pair, the female born two months ago produces her first pair also, making 5 pairs.
At the end of the nth month, the number of pairs of rabbits is equal to the number of new pairs (which is the number of pairs in month n − 2) plus the number of pairs alive last month (n − 1). This is the nth Fibonacci number.[12]
The name "Fibonacci sequence" was first used by the 19th-century number theorist Édouard Lucas.[13]
List of Fibonacci numbers
The first 21 Fibonacci numbers Fn for n = 0, 1, 2, ..., 20 are:[14]
F0 F1 F2 F3 F4 F5 F6 F7 F8 F9 F10 F11 F12 F13 F14 F15 F16 F17 F18 F19 F20 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765
The sequence can also be extended to negative index n using the re-arranged recurrence relation
which yields the sequence of "negafibonacci" numbers[15] satisfying
Thus the complete sequence is
F−8 F−7 F−6 F−5 F−4 F−3 F−2 F−1 F0 F1 F2 F3 F4 F5 F6 F7 F8 −21 13 −8 5 −3 2 −1 1 0 1 1 2 3 5 8 13 21
Occurrences in mathematics

The Fibonacci numbers occur in the sums of "shallow" diagonals in Pascal's triangle (see Binomial coefficient).[16]
The Fibonacci numbers can be found in different ways in the sequence of binary strings.
- The number of binary strings of length n without consecutive 1s is the Fibonacci number Fn+2. For example, out of the 16 binary strings of length 4, there are F6 = 8 without consecutive 1s – they are 0000, 1000, 0100, 0010, 1010, 0001, 1001 and 0101. By symmetry, the number of strings of length n without consecutive 0s is also Fn+2.
- The number of binary strings of length n without an odd number of consecutive 1s is the Fibonacci number Fn+1. For example, out of the 16 binary strings of length 4, there are F5 = 5 without an odd number of consecutive 1s – they are 0000, 0011, 0110, 1100, 1111.
- The number of binary strings of length n without an even number of consecutive 0s or 1s is 2Fn. For example, out of the 16 binary strings of length 4, there are 2F4 = 6 without an even number of consecutive 0s or 1s – they are 0001, 1000, 1110, 0111, 0101, 1010.
Relation to the golden ratio
Closed-form expression
Like every sequence defined by linear recurrence,[17] the Fibonacci numbers have a closed-form solution. It has become very well known as Binet's formula, even though it was already known by Abraham de Moivre:[citation needed]
where
is the golden ratio (sequence A001622 in the OEIS), and
To see this,[19] note that φ and ψ are both solutions of the equations
so the powers of φ and ψ satisfy the Fibonacci recursion. In other words
and
It follows that for any values a and b, the sequence defined by
satisfies the same recurrence
If a and b are chosen so that U0 = 0 and U1 = 1 then the resulting sequence Un must be the Fibonacci sequence. This is the same as requiring a and b satisfy the system of equations:
which has solution
producing the required formula.
Computation by rounding
Since
for all n ≥ 0, the number Fn is the closest integer to
Therefore it can be found by rounding, or in terms of the floor function:
Similarly, if we already know that the number F > 1 is a Fibonacci number, we can determine its index within the sequence by
Limit of consecutive quotients
Johannes Kepler observed that the ratio of consecutive Fibonacci numbers converges. He wrote that "as 5 is to 8 so is 8 to 13, practically, and as 8 is to 13, so is 13 to 21 almost", and concluded that the limit approaches the golden ratio .[20]
This convergence does not depend on the starting values chosen, excluding 0, 0. For example, the initial values 19 and 31 generate the sequence 19, 31, 50, 81, 131, 212, 343, 555 ... etc. The ratio of consecutive terms in this sequence shows the same convergence towards the golden ratio.
In fact this holds for any sequence which satisfies the Fibonacci recurrence other than a sequence of 0's. This can be derived from Binet's formula.
Decomposition of powers of the golden ratio
Since the golden ratio satisfies the equation
this expression can be used to decompose higher powers as a linear function of lower powers, which in turn can be decomposed all the way down to a linear combination of and 1. The resulting recurrence relationships yield Fibonacci numbers as the linear coefficients:
This expression is also true for if the Fibonacci sequence is extended to negative integers using the Fibonacci rule
Matrix form
A 2-dimensional system of linear difference equations that describes the Fibonacci sequence is
or
The eigenvalues of the matrix A are and , and the elements of the eigenvectors of A, and , are in the ratios and Using these facts, and the properties of eigenvalues, we can derive a direct formula for the nth element in the fibonacci series:
The matrix has a determinant of −1, and thus it is a 2×2 unimodular matrix. This property can be understood in terms of the continued fraction representation for the golden ratio:
The Fibonacci numbers occur as the ratio of successive convergents of the continued fraction for , and the matrix formed from successive convergents of any continued fraction has a determinant of +1 or −1.
The matrix representation gives the following closed expression for the Fibonacci numbers:
Taking the determinant of both sides of this equation yields Cassini's identity
Additionally, since for any square matrix A, the following identities can be derived:
In particular, with ,
Recognizing Fibonacci numbers
The question may arise whether a positive integer z is a Fibonacci number. Since is the closest integer to , the most straightforward, brute-force test is the identity
which is true if and only if z is a Fibonacci number. In this formula, can be computed rapidly using any of the previously discussed closed-form expressions.
One implication of the above expression is this: if it is known that a number z is a Fibonacci number, we may determine an n such that F(n) = z by the following:
Alternatively, a positive integer z is a Fibonacci number if and only if one of or is a perfect square.[21]
A slightly more sophisticated test uses the fact that the convergents of the continued fraction representation of are ratios of successive Fibonacci numbers. That is, the inequality
(with coprime positive integers p, q) is true if and only if p and q are successive Fibonacci numbers. From this one derives the criterion that z is a Fibonacci number if and only if the closed interval
contains a positive integer.[22] For , it is easy to show that this interval contains at most one integer, and in the event that z is a Fibonacci number, the contained integer is equal to the next successive Fibonacci number after z. Somewhat remarkably, this result still holds for the case , but it must be stated carefully since appears twice in the Fibonacci sequence, and thus has two distinct successors.
Identities
Most identities involving Fibonacci numbers draw from combinatorial arguments. F(n) can be interpreted as the number of sequences of 1s and 2s that sum to n − 1, with the convention that F(0) = 0, meaning no sum will add up to −1, and that F(1) = 1, meaning the empty sum will "add up" to 0. Here the order of the summands matters. For example, 1 + 2 and 2 + 1 are considered two different sums and are counted twice.
First identity
- For n > 1.
- The nth Fibonacci number is the sum of the previous two Fibonacci numbers.
| Proof |
|---|
|
We must establish that the sequence of numbers defined by the combinatorial interpretation above satisfy the same recurrence relation as the Fibonacci numbers (and so are indeed identical to the Fibonacci numbers). The set of F(n + 1) ways of making ordered sums of 1s and 2s that sum to n may be divided into two non-overlapping sets. The first set contains those sums whose first summand is 1; the remainder sums to n − 1, so there are F(n) sums in the first set. The second set contains those sums whose first summand is 2; the remainder sums to n − 2, so there are F(n − 1) sums in the second set. The first summand can only be 1 or 2, so these two sets exhaust the original set. Thus F(n + 1) = F(n) + F(n − 1). |
Second identity
The sum of the first n Fibonacci numbers is equal to the n+2nd Fibonacci number minus 1.[23] In symbols:
- The sum of the first n Fibonacci numbers is the (n + 2)nd Fibonacci number minus 1.
| Proof |
|---|
|
We count the number of ways summing 1s and 2s to n + 1 such that at least one of the summands is 2. As before, there are F(n + 2) ways summing 1s and 2s to n + 1 when n ≥ 0. Since there is only one sum of n + 1 that does not use any 2, namely 1 + ... + 1 (n + 1 terms), we subtract 1 from F(n + 2). Equivalently, we can consider the first occurrence of 2 as a summand. If, in a sum, the first summand is 2, then there are F(n) ways to the complete the counting for n − 1. If the second summand is 2 but the first is 1, then there are F(n − 1) ways to complete the counting for n − 2. Proceed in this fashion. Eventually we consider the (n + 1)th summand. If it is 2 but all of the previous n summands are 1s, then there are F(0) ways to complete the counting for 0. If a sum contains 2 as a summand, the first occurrence of such summand must take place in between the first and (n + 1)th position. Thus F(n) + F(n − 1) + ... + F(0) gives the desired counting. By induction:
|
Third identity
This identity has slightly different forms for Fj, depending on whether j is odd or even.
The sum of the first n − 1 Fibonacci numbers, Fj, such that j is odd, is the (2n)th Fibonacci number.
The sum of the first n Fibonacci numbers, Fj, such that j is even, is the (2n + 1)th Fibonacci number minus 1.
| Proofs |
|---|
|
1: j is odd By induction for F2n: A basis case for this could be F1 = F2. 2: j is even By induction for F2n+1: A basis case for this could be F0 = F1 − 1. |
| Alternative proof |
|---|
|
By using identity 1 we can construct a telescoping sum: If the summands are the Fibonacci numbers with even index, the proof is very similar. Summing both cases yields identity 2. |
Fourth identity
| Proof |
|---|
|
This identity can be established in two stages. First, we count the number of ways summing 1s and 2s to −1, 0, ..., or n + 1 such that at least one of the summands is 2. By our second identity, there are F(n + 2) − 1 ways summing to n + 1; F(n + 1) − 1 ways summing to n; ...; and, eventually, F(2) − 1 way summing to 1. As F(1) − 1 = F(0) = 0, we can add up all n + 1 sums and apply the second identity again to obtain
On the other hand, we observe from the second identity that there are
......
Adding up all n + 1 sums, we see that there are
Since the two methods of counting refer to the same number, we have
Finally, we complete the proof by subtracting the above identity from n + 1 times the second identity. |
Fifth identity
- The sum of the squares of the first n Fibonacci numbers is the product of the nth and (n + 1)th Fibonacci numbers.
| Proof |
|---|
|
Although this identity can be established by either induction or direct, albeit messy, algebraic manipulation, perhaps the most elegant and most insightful method is by a simple geometric argument. Consider the Fibonacci Rectangles constructed in previous sections. Using a common trick, we will compute the area of this rectangle in two different ways. But since this must yield the same answer in both cases, we know these resulting expressions must be equal, which will yield the desired identity. On the one hand, the n-th rectangle is composed of n squares, whose side lengths are F(1), F(2), ..., F(n). Its area is therefore the sum of each of these squares, which is given by On the other hand, we know that the n-th rectangle has side lengths F(n) and F(n + 1). Thus, its area is simply given by Setting these expressions equal to each other completes the proof. |
Identity for doubling n
Where is the n'th Lucas Number.
Another identity
Another identity useful for calculating Fn for large values of n is[25]
from which other identities for specific values of k, n, and c can be derived below, including
for all integers n and k. Doubling identities of this type can be used to calculate Fn using O(log n) long multiplication operations of size n bits. The number of bits of precision needed to perform each multiplication doubles at each step, so the performance is limited by the final multiplication; if the fast Schönhage–Strassen multiplication algorithm is used, this is O(n log n log log n) bit operations. Notice that, with the definition of Fibonacci numbers with negative n given in the introduction, this formula reduces to the double n formula when k = 0.
Other identities
Other identities include relationships to the Lucas numbers, which have the same recursive properties but start with L0 = 2 and L1 = 1. These properties include F2n = FnLn.
There are also scaling identities, which take you from Fn and Fn+1 to a variety of things of the form Fan+b; for instance
- by Cassini's identity.
These can be found experimentally using lattice reduction, and are useful in setting up the special number field sieve to factorize a Fibonacci number. Such relations exist in a very general sense for numbers defined by recurrence relations. See the section on multiplication formulae under Perrin numbers for details.
Power series
The generating function of the Fibonacci sequence is the power series
This series has a simple and interesting closed-form solution for :[26]
This solution can be proven by using the Fibonacci recurrence to expand each coefficient in the infinite sum defining :
Solving the equation for results in the closed form solution.
In particular, math puzzle-books note the curious value ,[27] or more generally
for all integers .
Conversely,
Reciprocal sums
Infinite sums over reciprocal Fibonacci numbers can sometimes be evaluated in terms of theta functions. For example, we can write the sum of every odd-indexed reciprocal Fibonacci number as
and the sum of squared reciprocal Fibonacci numbers as
If we add 1 to each Fibonacci number in the first sum, there is also the closed form
and there is a nice nested sum of squared Fibonacci numbers giving the reciprocal of the golden ratio,
Results such as these make it plausible that a closed formula for the plain sum of reciprocal Fibonacci numbers could be found, but none is yet known. Despite that, the reciprocal Fibonacci constant
has been proved irrational by Richard André-Jeannin.
Millin series gives a remarkable identity:[28]
which follows from the closed form for its partial sums as N tends to infinity:
Primes and divisibility
Divisibility properties
Every 3rd number of the sequence is even and more generally, every kth number of the sequence is a multiple of Fk. Thus the Fibonacci sequence is an example of a divisibility sequence. In fact, the Fibonacci sequence satisfies the stronger divisibility property
Fibonacci primes
A Fibonacci prime is a Fibonacci number that is prime (sequence A005478 in the OEIS). The first few are:
- 2, 3, 5, 13, 89, 233, 1597, 28657, 514229, ...
Fibonacci primes with thousands of digits have been found, but it is not known whether there are infinitely many.[29]
Fkn is divisible by Fn, so, apart from F4 = 3, any Fibonacci prime must have a prime index. As there are arbitrarily long runs of composite numbers, there are therefore also arbitrarily long runs of composite Fibonacci numbers.
With the exceptions of 1, 8 and 144 (F1 = F2, F6 and F12) every Fibonacci number has a prime factor that is not a factor of any smaller Fibonacci number (Carmichael's theorem).[30]
144 is the only nontrivial square Fibonacci number.[31] Attila Pethő proved[32] in 2001 that there are only finitely many perfect power Fibonacci numbers. In 2006, Y. Bugeaud, M. Mignotte, and S. Siksek proved that only 8 and 144 are non-trivial perfect powers.[33]
No Fibonacci number greater than F6 = 8 is one greater or one less than a prime number.[34]
Any three consecutive Fibonacci numbers, taken two at a time, are relatively prime: that is,
- gcd(Fn, Fn+1) = gcd(Fn, Fn+2) = 1.
More generally,
Prime divisors of Fibonacci numbers
The divisibility of Fibonacci numbers by a prime p is related to the Legendre symbol which is evaluated as follows:
If p is a prime number then [37][38]
For example,
It is not known whether there exists a prime p such that . Such primes (if there are any) would be called Wall–Sun–Sun primes.
Also, if p ≠ 5 is an odd prime number then:[39]
Examples of all the cases:
For odd n, all odd prime divisors of Fn are ≡ 1 (mod 4), implying that all odd divisors of Fn (as the products of odd prime divisors) are ≡ 1 (mod 4).[40][41]
For example,
F1 = 1, F3 = 2, F5 = 5, F7 = 13, F9 = 34 = 2×17, F11 = 89, F13 = 233, F15 = 610 = 2×5×61
Periodicity modulo n
It may be seen that if the members of the Fibonacci sequence are taken mod n, the resulting sequence must be periodic with period at most n2. The lengths of the periods for various n form the so-called Pisano periods (sequence A001175 in the OEIS). Determining the Pisano periods in general is an open problem,[citation needed] although for any particular n it can be solved as an instance of cycle detection.
Right triangles
Starting with 5, every second Fibonacci number is the length of the hypotenuse of a right triangle with integer sides, or in other words, the largest number in a Pythagorean triple. The length of the longer leg of this triangle is equal to the sum of the three sides of the preceding triangle in this series of triangles, and the shorter leg is equal to the difference between the preceding bypassed Fibonacci number and the shorter leg of the preceding triangle.
The first triangle in this series has sides of length 5, 4, and 3. Skipping 8, the next triangle has sides of length 13, 12 (5 + 4 + 3), and 5 (8 − 3). Skipping 21, the next triangle has sides of length 34, 30 (13 + 12 + 5), and 16 (21 − 5). This series continues indefinitely. The triangle sides a, b, c can be calculated directly:
These formulas satisfy for all n, but they only represent triangle sides when n > 2.
Any four consecutive Fibonacci numbers Fn, Fn+1, Fn+2 and Fn+3 can also be used to generate a Pythagorean triple in a different way[42]:
Example 1: let the Fibonacci numbers be 1, 2, 3 and 5. Then:
Magnitude
Since is asymptotic to , the number of digits in is asymptotic to . As a consequence, for every integer there are either 4 or 5 Fibonacci numbers with d decimal digits.
More generally, in the base b representation, the number of digits in is asymptotic to .
Applications
The Fibonacci numbers are important in the computational run-time analysis of Euclid's algorithm to determine the greatest common divisor of two integers: the worst case input for this algorithm is a pair of consecutive Fibonacci numbers.[43]
Yuri Matiyasevich was able to show that the Fibonacci numbers can be defined by a Diophantine equation, which led to his original solution of Hilbert's tenth problem.
The Fibonacci numbers are also an example of a complete sequence. This means that every positive integer can be written as a sum of Fibonacci numbers, where any one number is used once at most. Specifically, every positive integer can be written in a unique way as the sum of one or more distinct Fibonacci numbers in such a way that the sum does not include any two consecutive Fibonacci numbers. This is known as Zeckendorf's theorem, and a sum of Fibonacci numbers that satisfies these conditions is called a Zeckendorf representation. The Zeckendorf representation of a number can be used to derive its Fibonacci coding.
Fibonacci numbers are used by some pseudorandom number generators.
Fibonacci numbers are used in a polyphase version of the merge sort algorithm in which an unsorted list is divided into two lists whose lengths correspond to sequential Fibonacci numbers – by dividing the list so that the two parts have lengths in the approximate proportion φ. A tape-drive implementation of the polyphase merge sort was described in The Art of Computer Programming.
Fibonacci numbers arise in the analysis of the Fibonacci heap data structure.
The Fibonacci cube is an undirected graph with a Fibonacci number of nodes that has been proposed as a network topology for parallel computing.
A one-dimensional optimization method, called the Fibonacci search technique, uses Fibonacci numbers.[44]
The Fibonacci number series is used for optional lossy compression in the IFF 8SVX audio file format used on Amiga computers. The number series compands the original audio wave similar to logarithmic methods such as µ-law.[45][46]
In music, Fibonacci numbers are sometimes used to determine tunings, and, as in visual art, to determine the length or size of content or formal elements. It is commonly thought that the third movement of Béla Bartók's Music for Strings, Percussion, and Celesta was structured using Fibonacci numbers.
Since the conversion factor 1.609344 for miles to kilometers is close to the golden ratio (denoted φ), the decomposition of distance in miles into a sum of Fibonacci numbers becomes nearly the kilometer sum when the Fibonacci numbers are replaced by their successors. This method amounts to a radix 2 number register in golden ratio base φ being shifted. To convert from kilometers to miles, shift the register down the Fibonacci sequence instead.[47]
In nature
Fibonacci sequences appear in biological settings,[6] in two consecutive Fibonacci numbers, such as branching in trees, arrangement of leaves on a stem, the fruitlets of a pineapple,[7] the flowering of artichoke, an uncurling fern and the arrangement of a pine cone.[8] In addition, numerous poorly substantiated claims of Fibonacci numbers or golden sections in nature are found in popular sources, e.g., relating to the breeding of rabbits, the spirals of shells, and the curve of waves.[48] The Fibonacci numbers are also found in the family tree of honeybees.[49]
Przemysław Prusinkiewicz advanced the idea that real instances can in part be understood as the expression of certain algebraic constraints on free groups, specifically as certain Lindenmayer grammars.[50]

A model for the pattern of florets in the head of a sunflower was proposed by H. Vogel in 1979.[51] This has the form
where n is the index number of the floret and c is a constant scaling factor; the florets thus lie on Fermat's spiral. The divergence angle, approximately 137.51°, is the golden angle, dividing the circle in the golden ratio. Because this ratio is irrational, no floret has a neighbor at exactly the same angle from the center, so the florets pack efficiently. Because the rational approximations to the golden ratio are of the form F(j):F(j + 1), the nearest neighbors of floret number n are those at n ± F(j) for some index j which depends on r, the distance from the center. It is often said that sunflowers and similar arrangements have 55 spirals in one direction and 89 in the other (or some other pair of adjacent Fibonacci numbers), but this is true only of one range of radii, typically the outermost and thus most conspicuous.[52]
The bee ancestry code
Fibonacci numbers also appear in the description of the reproduction of a population of idealized honeybees, according to the following rules:
- If an egg is laid by an unmated female, it hatches a male or drone bee.
- If, however, an egg was fertilized by a male, it hatches a female.
Thus, a male bee will always have one parent, and a female bee will have two.
If one traces the ancestry of any male bee (1 bee), he has 1 parent (1 bee), 2 grandparents, 3 great-grandparents, 5 great-great-grandparents, and so on. This sequence of numbers of parents is the Fibonacci sequence. The number of ancestors at each level, Fn, is the number of female ancestors, which is Fn−1, plus the number of male ancestors, which is Fn−2.[53] (This is under the unrealistic assumption that the ancestors at each level are otherwise unrelated.)
Popular culture
Generalizations
The Fibonacci sequence has been generalized in many ways. These include:
- Generalizing the index to negative integers to produce the Negafibonacci numbers.
- Generalizing the index to real numbers using a modification of Binet's formula.[25]
- Starting with other integers. Lucas numbers have L1 = 1, L2 = 3, and Ln = Ln−1 + Ln−2. Primefree sequences use the Fibonacci recursion with other starting points in order to generate sequences in which all numbers are composite.
- Letting a number be a linear function (other than the sum) of the 2 preceding numbers. The Pell numbers have Pn = 2Pn – 1 + Pn – 2.
- Not adding the immediately preceding numbers. The Padovan sequence and Perrin numbers have P(n) = P(n – 2) + P(n – 3).
- Generating the next number by adding 3 numbers (tribonacci numbers), 4 numbers (tetranacci numbers), or more. The resulting sequences are known as n-Step Fibonacci numbers.[54]
- Adding other objects than integers, for example functions or strings—one essential example is Fibonacci polynomials.
See also
Notes
- ^ Lucas p. 3
- ^ a b Sigler, Laurence E. (trans.) (2002). Fibonacci's Liber Abaci. Springer-Verlag. ISBN 0-387-95419-8. Chapter II.12, pp. 404–405.
- ^ a b Susantha Goonatilake (1998). Toward a Global Science. Indiana University Press. p. 126. ISBN 9780253333889.
- ^ a b Singh, Parmanand (1985). "The So-called Fibonacci numbers in ancient and medieval India". Historia Mathematica. 12 (3): 229–244. doi:10.1016/0315-0860(85)90021-7.
- ^ a b Donald Knuth (2006). The Art of Computer Programming: Generating All Trees—History of Combinatorial Generation; Volume 4. Addison–Wesley. p. 50. ISBN 9780321335708. quote: it was natural to consider the set of all sequences of [L] and [S] that have exactly m beats. ... there are exactly Fm+1 of them. For example the 21 sequences when m = 7 are: [gives list]. In this way Indian prosodists were led to discover the Fibonacci sequence, as we have observed in Section 1.2.8 (from v.1)
- ^ a b S. Douady and Y. Couder (1996). "Phyllotaxis as a Dynamical Self Organizing Process" (PDF). Journal of Theoretical Biology. 178 (178): 255–274. doi:10.1006/jtbi.1996.0026.
- ^ a b Jones, Judy (2006). "Science". An Incomplete Education. Ballantine Books. p. 544. ISBN 978-0-7394-7582-9.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ a b A. Brousseau (1969). "Fibonacci Statistics in Conifers". Fibonacci Quarterly (7): 525–532.
- ^ Donald Knuth (1968). The Art Of Computer Programming, Volume 1. Addison Wesley. ISBN 8177587544.quote: "Before Fibonacci wrote his work, the sequence Fn had already been discussed by Indian scholars, who had long been interested in rhythmic patterns... both Gopala (before 1135AD) and Hemachandra (c.1150) mentioned the numbers 1,2,3,5,8,13,21 explicitly. [See P. Singh Historia Math 12 (1985) 229–244]" p. 100 (3d ed)...
- ^ [Agrawala. V. S. 1969]. pAninikAlIna bhAratavarSha (Hn.). Varanasi-I: TheChowkhamba Vidyabhawan.
- ^ Velankar, H. D. (1962.). _Vr^ttajAtisamuccaya_ of kavi Virahanka. Rajasthan Oriental Research Institute, Jodhpur.
{{cite book}}: Check date values in:|year=(help)CS1 maint: year (link) p.101. quote: " For four, variations of meters of two [and] three being mixed, five happens. For five, variations of two earlier – three [and] four, being mixed, eight is obtained.- In this way, for six, [variations] of four [and] of five being mixed, thirteen happens. And like that, variations of two earlier meters being mixed, seven morae [is] twenty-one. In this way, the process should be
- ^ Knott, Ron. "Fibonacci's Rabbits". University of Surrey Faculty of Engineering and Physical Sciences.
- ^ Martin Gardner (1996). Mathematical Circus. The Mathematical Association of America. ISBN 0883855062.quote: "It is ironic that Leonardo, who made valuable contributions to mathematics, is remembered today mainly because a 19th-century French number theorist, Edouard Lucas ... attached the name Fibonacci to a number sequence that appears in a trivial problem in Liber abaci." p.153
- ^ The website [1] has the first 300 Fn factored into primes and links to more extensive tables.
- ^ Knuth, Donald. "Negafibonacci Numbers and the Hyperbolic Plane" Paper presented at the annual meeting of the Mathematical Association of America, The Fairmont Hotel, San Jose, CA. 2008-12-11 <http://www.allacademic.com/meta/p206842_index.html>
- ^ Lucas p. 7
- ^ Greene, Daniel H.; Knuth, Donald E. (1982). "Mathematics for the Analysis of Algorithms" (Document). Birkhäuser. p. 17.
{{cite document}}: Unknown parameter|contribution=ignored (help); Unknown parameter|edition=ignored (help) - ^ Ball p. 156
- ^ Following Ball p. 155-156
- ^ Kepler, Johannes (1966). A New Year Gift: On Hexagonal Snow. Oxford University Press. p. 92. ISBN 0198581203. Strena seu de Nive Sexangula (1611).
- ^ Posamentier, Alfred (2007). The (Fabulous) FIBONACCI Numbers. Prometheus Books. p. 305. ISBN 978-1-59102-475-0.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ M. Möbius, Wie erkennt man eine Fibonacci Zahl?, Math. Semesterber. (1998) 45; 243–246.
- ^ Lucas p. 4
- ^ Vorobiev, Nikolaĭ Nikolaevich (2002). "Chapter 1". Fibonacci Numbers. Birkhäuser. pp. 5–6. ISBN 3-7643-6135-2.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ a b c Weisstein, Eric W. "Fibonacci Number". MathWorld.
- ^ Glaister, P.. Fibonacci power series. The Mathematical Gazette, 1995, p. 521.
- ^ The Remarkable Number 1/89 at The Geometry Center.
- ^ Weisstein, Eric W. "Millin Series". MathWorld.
- ^ Weisstein, Eric W. "Fibonacci Prime". MathWorld.
- ^ Ron Knott, "The Fibonacci numbers".
- ^ J H E Cohn (1964). "Square Fibonacci Numbers Etc". Fibonacci Quarterly. 2: 109–113.
- ^ A. Pethő, Diophantine properties of linear recursive sequences II, Acta Math. Paedagogicae Nyíregyháziensis, 17(2001), 81–96.
- ^ Y. Bugeaud, M. Mignotte, S. Siksek: Classical and modular approaches to exponential Diophantine equations. I. Fibonacci and Lucas perfect powers. Ann. Math. (2), 163(2006), 969–1018.
- ^ Ross Honsberger Mathematical Gems III (AMS Dolciani Mathematical Expositions No. 9), 1985, ISBN 0-88385-318-3, p. 133.
- ^ Paulo Ribenboim, My Numbers, My Friends, Springer-Verlag 2000.
- ^ Su, Francis E., et al. "Fibonacci GCD's, please.", Mudd Math Fun Facts.
- ^ Paulo Ribenboim (1996), The New Book of Prime Number Records, New York: Springer, ISBN 0-387-94457-5, p. 64.
- ^ Franz Lemmermeyer (2000), Reciprocity Laws, New York: Springer, ISBN 3-540-66957-4, ex 2.25–2.28, pp. 73–74.
- ^ Lemmermeyer, ex. 2.28, pp. 73–74.
- ^ Lemmermeyer, ex. 2.27 p. 73.
- ^ The website [2] has the first 300 Fibonacci numbers factored into primes.
- ^ Koshy, Thomas (2007). Elementary number theory with applications. Academic Press. p. 581. ISBN 0123724872.
- ^ Knuth, Donald E. (1997). The Art of Computer Programming, Volume 1: Fundamental Algorithms (3rd ed.). Addison–Wesley. ISBN 0-201-89683-4. (p. 343).
- ^ M. Avriel and D.J. Wilde (1966). "Optimality of the Symmetric Fibonacci Search Technique". Fibonacci Quarterly (3): 265–269.
- ^ Amiga ROM Kernel Reference Manual, Addison–Wesley 1991.
- ^ IFF – MultimediaWiki.
- ^ Zeckendorf representation.
- ^ "Fibonacci Flim-Flam".
- ^ "Marks for the da Vinci Code: B–". Computer Science For Fun: CS4FN.
- ^ Prusinkiewicz, Przemyslaw (1989). Lindenmayer Systems, Fractals, and Plants (Lecture Notes in Biomathematics). Springer-Verlag. ISBN 0-387-97092-4.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ Vogel, H (1979). "A better way to construct the sunflower head". Mathematical Biosciences. 44 (44): 179–189. doi:10.1016/0025-5564(79)90080-4.
- ^ Prusinkiewicz, Przemyslaw (1990). [[The Algorithmic Beauty of Plants]]. Springer-Verlag. pp. 101–107. ISBN 978-0387972978.
{{cite book}}: URL–wikilink conflict (help); Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ The Fibonacci Numbers and the Ancestry of Bees.
- ^ Weisstein, Eric W. "Fibonacci n-Step Number". MathWorld.
Template:Inconsistent citations
References
- Ball, Keith M. (2003). "Chapter 8: Fibonacci's Rabbits Revisited". Strange Curves, Counting Rabbits, and Other Mathematical Explorations. Princeton University Press. ISBN 0691113211.
- Lucas, Édouard (1891). Théorie des nombres. Vol. 1. Gauthier-Villars.
External links
- Fibonacci Sequence on In Our Time at the BBC
- Sequence OEIS: A000045 Fibonacci Numbers at the On-Line Encyclopedia of Integer Sequences
- Periods of Fibonacci Sequences Mod m at MathPages
- Scientists find clues to the formation of Fibonacci spirals in nature
- Implementation to calculate Fibonacci sequence in Lisp





















































![{\displaystyle {\bigg [}\varphi z-{\frac {1}{z}},\varphi z+{\frac {1}{z}}{\bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14edda62f581eb4023de98ff582af9a5cf01aae5)






















![{\displaystyle \sum _{i=0}^{n-1}F_{2i+1}=\sum _{i=0}^{n-1}[F_{2(i+1)}-F_{2i}]=F_{2n}-F_{0}=F_{2n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2dccea9c790fa1e5e033c29f8282fe242f865d13)






























































