Community structure: Difference between revisions
Aaron McDaid (talk | contribs) →Surprise maximization: Beating modularity is easy. Everyone and their dog (including me!) has done so. |
Aaron McDaid (talk | contribs) →Surprise maximization: Modularity does take account of the number of nodes (indirectly, via the total degree of the nodes). Modularity is awful, I agree, but let's not misrepresent it. |
||
| Line 158: | Line 158: | ||
===Surprise maximization=== |
===Surprise maximization=== |
||
Another approach to detect community structure is the maximization of [[Surprise (networks)|Surprise]] (''S'').<ref name = "Surprise" /> ''S'' evaluates the quality of a partition of a network into communities using a cumulative hypergeometric distribution. Surprise maximization, like many other non-modularity methods, outperforms modularity maximization, <ref name = "Surprise" /> |
Another approach to detect community structure is the maximization of [[Surprise (networks)|Surprise]] (''S'').<ref name = "Surprise" /> ''S'' evaluates the quality of a partition of a network into communities using a cumulative hypergeometric distribution. Surprise maximization, like many other non-modularity methods, outperforms modularity maximization, <ref name = "Surprise" />. Several algorithms use Surprise maximization to obtain the best partitions in trees obtained by hierarchical consensus clustering of a graph <ref name = "jerarca"> |
||
{{cite journal |
{{cite journal |
||
| author = Rodrigo Aldecoa and Ignacio Marín |
| author = Rodrigo Aldecoa and Ignacio Marín |
||
Revision as of 15:05, 4 March 2013
| Part of a series on | ||||
| Network science | ||||
|---|---|---|---|---|
| Network types | ||||
| Graphs | ||||
|
||||
| Models | ||||
|
||||
| ||||
In the study of complex networks, a network is said to have community structure if the nodes of the network can be easily grouped into (potentially overlapping) sets of nodes such that each set of nodes is densely connected internally. In the particular case of non-overlapping community finding, this implies that the network divides naturally into groups of nodes with dense connections internally and sparser connections between groups. But overlapping communities are also allowed. The more general definition is based on the principle that pairs of nodes are more likely to be connected if they are both members of the same community(ies), and less likely to be connected if they do not share communities.
Properties
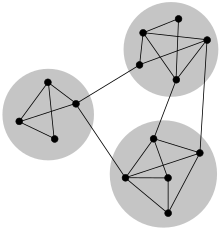
In the study of networks, such as computer and information networks, social networks or biological networks, a number of different characteristics have been found to occur commonly, including the small-world property, heavy-tailed degree distributions, and clustering, among others. Another common characteristic is community structure [1] [2] [3] . In the context of networks, community structure refers to the occurrence of groups of nodes in a network that are more densely connected internally than with the rest of the network, as shown in the example image to the right. This inhomogeneity of connections suggests that the network has certain natural divisions within it. The communities are often defined in terms of the partition of the set of vertices, that is each node is put into one and only one community, just as in the figure. This is a useful simplification but may not be appropriate in many cases. Not all networks need display community structure. Many model networks, for example, such as the random graph and the Barabási–Albert model, do not display community structure.
Applications
Community structures are quite common in real networks. Social networks often include community groups (the origin of the term, in fact) based on common location, interests, occupation, etc. Metabolic networks have communities based on functional groupings. Citation networks form communities by research topic.[1] Being able to identify these sub-structures within a network can provide insight into how network function and topology affect each other.
Algorithms for finding communities
Finding communities within an arbitrary network can be a computationally difficult task. The number of communities, if any, within the network is typically unknown and the communities are often of unequal size and/or density. Despite these difficulties, however, several methods for community finding have been developed and employed with varying levels of success.[3]
Minimum-cut method
One of the oldest algorithms for dividing networks into parts is the minimum-cut method (and variants such as ratio cut and normalized cut). This method sees use, for example, in load balancing for parallel computing in order to minimize communication between processor nodes.
In the minimum-cut method, the network is divided into a predetermined number of parts, usually of approximately the same size, chosen such that the number of edges between groups is minimized. The method works well in many of the applications for which it was originally intended but is less than ideal for finding community structure in general networks since it will find communities regardless of whether they are implicit in the structure, and it will find only a fixed number of them. [4]
Hierarchical clustering
Another method for finding community structures in networks is hierarchical clustering. In this method one defines a similarity measure quantifying some (usually topological) type of similarity between node pairs. Commonly used measures include the cosine similarity, the Jaccard index, and the Hamming distance between rows of the adjacency matrix. Then one groups similar nodes into communities according to this measure. There are several common schemes for performing the grouping, the two simplest being single-linkage clustering, in which two groups are considered separate communities if and only if all pairs of nodes in different groups have similarity lower than a given threshold, and complete linkage clustering, in which all nodes within every group have similarity greater than threshold.
Girvan–Newman algorithm
Another commonly used algorithm for finding communities is the Girvan–Newman algorithm.[1] This algorithm identifies edges in a network that lie between communities and then removes them, leaving behind just the communities themselves. The identification is performed by employing the graph-theoretic measure betweenness, which assigns a number to each edge which is large if the edge lies "between" many pairs of nodes.
The Girvan–Newman algorithm returns results of reasonable quality and is popular because it has been implemented in a number of standard software packages. But it also runs slowly, taking time O(m2n) on a network of n vertices and m edges, making it impractical for networks of more than a few thousand nodes .[5]
Modularity maximization
In spite of its known drawbacks, one of the most widely used methods for community detection is modularity maximization.[5] Modularity is a benefit function that measures the quality of a particular division of a network into communities. The modularity maximization method detects communities by searching over possible divisions of a network for one or more that have particularly high modularity. Since exhaustive search over all possible divisions is usually intractable, practical algorithms are based on approximate optimization methods such as greedy algorithms, simulated annealing, or spectral optimization, with different approaches offering different balances between speed and accuracy. [6]. A popular modularity maximization approach is the Louvain method, which iteratively optimizes local communities until global modularity can no longer be improved given perturbations to the current community state.[7]
The usefulness of modularity optimization is however questionable: on the one hand, it has been shown that modularity optimization often fails to detect clusters smaller than some scale, depending on the size of the network (resolution limit [8] ); on the other hand the landscape of modularity values is characterized by a huge degeneracy of partitions with high modularity, close to the absolute maximum, which may be very different from each other .[9] It is also significant that surprise maximization (see below) has been shown to perform better than modularity maximization in benchmarks consisting in networks of known structure .[10]
Surprise maximization
Another approach to detect community structure is the maximization of Surprise (S).[10] S evaluates the quality of a partition of a network into communities using a cumulative hypergeometric distribution. Surprise maximization, like many other non-modularity methods, outperforms modularity maximization, [10]. Several algorithms use Surprise maximization to obtain the best partitions in trees obtained by hierarchical consensus clustering of a graph [11]. Among them, the best known is the oldest, called UVCLUSTER [12], which has been used in several papers to obtain data from empirical networks (e. g. protein-interaction networks; protein domain networks) and cited in more than one hundred articles [13].
Clique based methods
Cliques are subgraphs in which every node is connected to every other node in the clique. As nodes can not be more tightly connected than this, it is not surprising that there are many approaches to community detection in networks based on the detection of cliques in a graph and the analysis of how these overlap. Note that as a node can be a member of more than one clique, a node can be a member of more than one community in these methods giving an overlapping community structure.
One approach is to find the maximal cliques, that is find the cliques which are not the subgraph of any other clique. The classic algorithm to find these is the Bron-Kerbosch algorithm. The overlap of these can be used to define communities in several ways. The simplest is to consider only maximal cliques bigger than a minimum size (number of nodes). The union of these cliques then defines a subgraph whose components (disconnected parts) then define communities.[14] Such approaches are often implemented in social network analysis software such as UCInet.
The alternative approach to is to use cliques of fixed size, k. The overlap of these can be used to define a type of k-regular hypergraph or a structure which is a generalisation of the line graph (the case when k=2) known as a Clique graph.[15] The clique graphs have vertices which represent the cliques in the original graph while the edges of the clique graph record the overlap of the clique in the original graph. Applying any of the previous community detection methods (which assign each node to a community) to the clique graph then assigns each clique to a community. This can then be used to determine community membership of nodes in the cliques. Again as a node may be in several cliques, it can be a member of several communities. For instance the clique percolation method[16] defines communities as percolation clusters of k-cliques. To do this it finds all k-cliques in a network, that is all the complete sub-graphs of k-nodes. It then defines two k-cliques to be adjacent if they share k − 1 nodes, that is this is used to define edges in a clique graph. A community is then defined to be the maximal union of k-cliques in which we can reach any k-clique from any other k-clique through series of k-clique adjacencies. That is communities are just the connected components in the clique graph. Since a node can belong to several different k-clique percolation clusters at the same time, the communities can overlap with each other.
Testing methods of finding communities algorithms
The evaluation of algorithms, to detect which are better at detecting community structure, is still an open question. It must be based on analyses of networks of known structure. A typical example is the "four groups" test, in which a network is divided into four equally-sized groups (usually of 32 nodes each) and the probabilities of connection within and between groups varied to create more or less challenging structures for the detection algorithm. Such benchmark graphs are a special case of the planted l-partition model [17] of Condon and Karp, or more generally of "stochastic block models," a general class of random network models containing community structure. Other more flexible benchmarks have been proposed that allow for varying group sizes and nontrivial degree distributions, such as LFR benchmark proposed by Lancichinetti et al. ,[18] which is an extension of the four groups benchmark that includes heterogeneous distributions of node degree and community size, making it a more severe test of community detection methods.
Commonly used computer-generated benchmarks start with a network of well-defined communities. Then, this structure is degraded by rewiring or removing links and it gets harder and harder for the algorithms to detect the original partition. At the end, the network reaches a point where it is essentially random. This kind of benchmark may be called "open". The performance on these benchmarks is evaluated by measures such as normalized mutual information or variation of information. They compare the solution obtained by an algorithm with the original community structure, evaluating the similarity of both partitions. While this is a reasonable approach when the original structure has been slightly blurred, it becomes pointless if it has been greatly modified, since the original community structure is not present anymore. Recently, Aldecoa and Marín have proposed the closed benchmarks.[19] They also start with a network with well-known community structure. However, the rewiring process is now guided toward a second structure which is identical to the initial one, although the node labels have been mapped from the former to the latter. In this manner, it can be tested if the solutions of the algorithms follow the evolution of the community structure or not. Moreover, the characteristic configuration of the closed benchmarks allows to check the optimality of an obtained partition, at any moment of the process, using the variation of information.
See also
External links
- Bibliography of community structure links
- Review article Community Detection in Graphs
- Survey article Communities in Networks (Notices of the American Mathematical Society, 10/09)
- Community Structure on arxiv.org
References
- ^ a b c M. Girvan and M. E. J. Newman (2002). "Community structure in social and biological networks". Proc. Natl. Acad. Sci. USA. 99 (12): 7821–7826. doi:10.1073/pnas.122653799. PMC 122977. PMID 12060727.
- ^ S. Fortunato (2010). "Community detection in graphs". Phys. Rep. 486 (3–5): 75–174. doi:10.1016/j.physrep.2009.11.002.
- ^ a b M. A. Porter, J.-P. Onnela and P. J. Mucha (2009). "Communities in Networks" (PDF). Not. Amer. Math. Soc. 56: 1082–1097, 1164–1166.
- ^ M. E. J. Newman (2004). "Detecting community structure in networks". Eur. Phys. J. B. 38 (2): 321–330. doi:10.1140/epjb/e2004-00124-y.
- ^ a b M. E. J. Newman (2004). "Fast algorithm for detecting community structure in networks". Phys. Rev. E. 69 (6): 066133. doi:10.1103/PhysRevE.69.066133.
- ^
L. Danon, J. Duch, A. Díaz-Guilera and A. Arenas (2005). "Comparing community structure identification". J. Stat. Mech. 2005 (09): P09008. doi:10.1088/1742-5468/2005/09/P09008.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^
V.D. Blondel, J.-L. Guillaume, R. Lambiotte and E. Lefebvre (2008). "Fast unfolding of community hierarchies in large networks". J. Stat. Mech. 2008 (10): P10008. doi:10.1088/1742-5468/2008/10/P10008.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ S. Fortunato and M. Barthelemy (2007). "Resolution limit in community detection". Proceedings of the National Academy of Science of the USA. 104 (1): 36–41. doi:10.1073/pnas.0605965104. PMC 1765466. PMID 17190818.
- ^ B. H. Good, Y.-A. de Montjoye and A. Clauset (2010). "The performance of modularity maximization in practical contexts". Phys. Rev. E. 81 (4): 046106. doi:10.1103/PhysRevE.81.046106.
- ^ a b c
Rodrigo Aldecoa and Ignacio Marín (2011). "Deciphering network community structure by Surprise". PLoS ONE. 6 (9): e24195. doi:10.1371/journal.pone.0024195. PMID 21909420.
{{cite journal}}: CS1 maint: unflagged free DOI (link) - ^
Rodrigo Aldecoa and Ignacio Marín (2010). "Jerarca: Efficient Analysis of Complex Networks Using Hierarchical Clustering". PLoS ONE. 5: e11585. doi:10.1371/journal.pone.0011585.
{{cite journal}}: CS1 maint: unflagged free DOI (link) - ^ Vicente Arnau, Sergio Mars and Ignacio Marín (2005). "Iterative Cluster Analysis of Protein Interaction Data". Bioinformatics. 21: 364–378. doi:10.1093/bioinformatics/bti021.
- ^ (http://scholar.google.com/scholar?cites=5396059551679935817&as_sdt=2005&sciodt=0,5&hl=en)
- ^ M.G. Everett and S.P. Borgatti (1998). "Analyzing Clique Overlap Connections". Connections. 21: 49.
- ^ T.S. Evans (2010). "Clique Graphs and Overlapping Communities". J. Stat. Mech.: P12037. arXiv:arXiv:1009.0638. doi:10.1088/1742-5468/2010/12/P12037.
{{cite journal}}: Check|arxiv=value (help) - ^
G. Palla, I. Derényi, I. Farkas and T. Vicsek (2005). "Uncovering the overlapping community structure of complex networks in nature and society". Nature. 435 (7043): 814–818. doi:10.1038/nature03607. PMID 15944704.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ Condon, A.; Karp, R. M. (2001). "Algorithms for graph partitioning on the planted partition model". Random Struct. Algor. 18 (2): 116–140. doi:10.1002/1098-2418(200103)18:2<116::AID-RSA1001>3.0.CO;2-2.
- ^ A. Lancichinetti, S. Fortunato and F. Radicchi (2008). "Benchmark graphs for testing community detection algorithms". Phys. Rev. E. 78 (4): 046110. doi:10.1103/PhysRevE.78.046110.
- ^ Rodrigo Aldecoa and Ignacio Marín (2012). "Closed benchmarks for network community structure characterization". Physical Review E. 85 (2): 026109. arXiv:1202.5909. doi:10.1103/PhysRevE.85.026109.

