Scale-free network

| Part of a series on | ||||
| Network science | ||||
|---|---|---|---|---|
| Network types | ||||
| Graphs | ||||
|
||||
| Models | ||||
|
||||
| ||||
A scale-free network is a network whose degree distribution follows a power law, at least asymptotically. That is, the fraction P(k) of nodes in the network having k connections to other nodes goes for large values of k as
where is a parameter whose value is typically in the range (wherein the second moment (scale parameter) of is infinite but the first moment is finite), although occasionally it may lie outside these bounds.[1][2] The name "scale-free" could be explained by the fact that some moments of the degree distribution are not defined, so that the network does not have a characteristic scale or "size".
Many networks have been reported to be scale-free, although statistical analysis has refuted many of these claims and seriously questioned others.[3][4] Additionally, some have argued that simply knowing that a degree-distribution is fat-tailed is more important than knowing whether a network is scale-free according to statistically rigorous definitions.[5][6] Preferential attachment and the fitness model have been proposed as mechanisms to explain conjectured power law degree distributions in real networks. Alternative models such as super-linear preferential attachment and second-neighbour preferential attachment may appear to generate transient scale-free networks, but the degree distribution deviates from a power law as networks become very large.[7][8]
History[edit]
In studies of the networks of citations between scientific papers, Derek de Solla Price showed in 1965 that the number of links to papers—i.e., the number of citations they receive—had a heavy-tailed distribution following a Pareto distribution or power law, and thus that the citation network is scale-free. He did not however use the term "scale-free network", which was not coined until some decades later. In a later paper in 1976, Price also proposed a mechanism to explain the occurrence of power laws in citation networks, which he called "cumulative advantage" but which is today more commonly known under the name preferential attachment.
Recent interest in scale-free networks started in 1999 with work by Albert-László Barabási and Réka Albert at the University of Notre Dame who mapped the topology of a portion of the World Wide Web,[9] finding that some nodes, which they called "hubs", had many more connections than others and that the network as a whole had a power-law distribution of the number of links connecting to a node. After finding that a few other networks, including some social and biological networks, also had heavy-tailed degree distributions, Barabási and Réka Albert coined the term "scale-free network" to describe the class of networks that exhibit a power-law degree distribution. However, studying seven examples of networks in social, economic, technological, biological, and physical systems, Amaral et al. were not able to find a scale-free network among these seven examples. Only one of these examples, the movie-actor network, had degree distribution P(k) following a power law regime for moderate k, though eventually this power law regime was followed by a sharp cutoff showing exponential decay for large k.[10]
Barabási and Réka Albert proposed a generative mechanism to explain the appearance of power-law distributions, which they called "preferential attachment" and which is essentially the same as that proposed by Price. Analytic solutions for this mechanism (also similar to the solution of Price) were presented in 2000 by Dorogovtsev, Mendes and Samukhin[11] and independently by Krapivsky, Redner, and Leyvraz, and later rigorously proved by mathematician Béla Bollobás.[12] Notably, however, this mechanism only produces a specific subset of networks in the scale-free class, and many alternative mechanisms have been discovered since.[13]
The history of scale-free networks also includes some disagreement. On an empirical level, the scale-free nature of several networks has been called into question. For instance, the three brothers Faloutsos believed that the Internet had a power law degree distribution on the basis of traceroute data; however, it has been suggested that this is a layer 3 illusion created by routers, which appear as high-degree nodes while concealing the internal layer 2 structure of the ASes they interconnect. [14]
On a theoretical level, refinements to the abstract definition of scale-free have been proposed. For example, Li et al. (2005) offered a potentially more precise "scale-free metric". Briefly, let G be a graph with edge set E, and denote the degree of a vertex (that is, the number of edges incident to ) by . Define
This is maximized when high-degree nodes are connected to other high-degree nodes. Now define
where smax is the maximum value of s(H) for H in the set of all graphs with degree distribution identical to that of G. This gives a metric between 0 and 1, where a graph G with small S(G) is "scale-rich", and a graph G with S(G) close to 1 is "scale-free". This definition captures the notion of self-similarity implied in the name "scale-free".
Overview[edit]
When the concept of "scale-free" was initially introduced in the context of networks,[9] it primarily referred to a specific trait: a power-law distribution for a given variable , expressed as . This property maintains its form when subjected to a continuous scale transformation , evoking parallels with the renormalization group techniques in statistical field theory.[15][16]
However, there's a key difference. In statistical field theory, the term "scale" often pertains to system size. In the realm of networks, "scale" is a measure of connectivity, generally quantified by a node's degree—that is, the number of links attached to it. Networks featuring a higher number of high-degree nodes are deemed to have greater connectivity.
The power-law degree distribution enables us to make "scale-free" assertions about the prevalence of high-degree nodes.[17] For instance, we can say that "nodes with triple the average connectivity occur half as frequently as nodes with average connectivity." The specific numerical value of what constitutes "average connectivity" becomes irrelevant, whether it's a hundred or a million.[18]
Characteristics[edit]
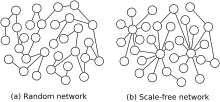
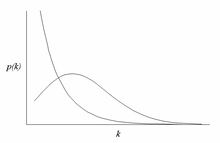
The most notable characteristic in a scale-free network is the relative commonness of vertices with a degree that greatly exceeds the average. The highest-degree nodes are often called "hubs", and are thought to serve specific purposes in their networks, although this depends greatly on the domain.
Clustering[edit]
Another important characteristic of scale-free networks is the clustering coefficient distribution, which decreases as the node degree increases. This distribution also follows a power law. This implies that the low-degree nodes belong to very dense sub-graphs and those sub-graphs are connected to each other through hubs. Consider a social network in which nodes are people and links are acquaintance relationships between people. It is easy to see that people tend to form communities, i.e., small groups in which everyone knows everyone (one can think of such community as a complete graph). In addition, the members of a community also have a few acquaintance relationships to people outside that community. Some people, however, are connected to a large number of communities (e.g., celebrities, politicians). Those people may be considered the hubs responsible for the small-world phenomenon.
At present, the more specific characteristics of scale-free networks vary with the generative mechanism used to create them. For instance, networks generated by preferential attachment typically place the high-degree vertices in the middle of the network, connecting them together to form a core, with progressively lower-degree nodes making up the regions between the core and the periphery. The random removal of even a large fraction of vertices impacts the overall connectedness of the network very little, suggesting that such topologies could be useful for security, while targeted attacks destroys the connectedness very quickly. Other scale-free networks, which place the high-degree vertices at the periphery, do not exhibit these properties. Similarly, the clustering coefficient of scale-free networks can vary significantly depending on other topological details.
Immunization[edit]
The question of how to immunize efficiently scale free networks which represent realistic networks such as the Internet and social networks has been studied extensively. One such strategy is to immunize the largest degree nodes, i.e., targeted (intentional) attacks since for this case p is relatively high and less nodes are needed to be immunized. However, in many realistic cases the global structure is not available and the largest degree nodes are not known.
Properties of random graph may change or remain invariant under graph transformations. Mashaghi A. et al., for example, demonstrated that a transformation which converts random graphs to their edge-dual graphs (or line graphs) produces an ensemble of graphs with nearly the same degree distribution, but with degree correlations and a significantly higher clustering coefficient. Scale free graphs, as such, remain scale free under such transformations.[19]
Examples[edit]
Although many real-world networks are thought to be scale-free, the evidence often remains inconclusive, primarily due to the developing awareness of more rigorous data analysis techniques.[3] As such, the scale-free nature of many networks is still being debated by the scientific community. A few examples of networks claimed to be scale-free include:
- Some Social networks, including collaboration networks. Two examples that have been studied extensively are the collaboration of movie actors in films and the co-authorship by mathematicians of papers.
- Many kinds of computer networks, including the internet and the webgraph of the World Wide Web.
- Some financial networks such as interbank payment networks [20][21]
- Protein–protein interaction networks.
- Semantic networks.[22]
- Airline networks.

Scale free topology has been also found in high temperature superconductors.[23] The qualities of a high-temperature superconductor — a compound in which electrons obey the laws of quantum physics, and flow in perfect synchrony, without friction — appear linked to the fractal arrangements of seemingly random oxygen atoms and lattice distortion.[24]
A space-filling cellular structure, weighted planar stochastic lattice (WPSL) has recently been proposed whose coordination number distribution follow a power-law. It implies that the lattice has a few blocks which have astonishingly large number neighbors with whom they share common borders. Its construction starts with an initiator, say a square of unit area, and a generator that divides it randomly into four blocks. The generator thereafter is sequentially applied over and over again to only one of the available blocks picked preferentially with respect to their areas. It results in the partitioning of the square into ever smaller mutually exclusive rectangular blocks. The dual of the WPSL (DWPSL), which is obtained by replacing each block with a node at its center, and each common border between blocks with an edge joining the two corresponding vertices, emerges as a network whose degree distribution follows a power-law.[25][26] The reason for it is that it grows following mediation-driven attachment model rule which also embodies preferential attachment rule but in disguise.
Generative models[edit]
Scale-free networks do not arise by chance alone. Erdős and Rényi (1960) studied a model of growth for graphs in which, at each step, two nodes are chosen uniformly at random and a link is inserted between them. The properties of these random graphs are different from the properties found in scale-free networks, and therefore a model for this growth process is needed.
The most widely known generative model for a subset of scale-free networks is Barabási and Albert's (1999) rich get richer generative model in which each new Web page creates links to existing Web pages with a probability distribution which is not uniform, but proportional to the current in-degree of Web pages. This model was originally invented by Derek J. de Solla Price in 1965 under the term cumulative advantage, but did not reach popularity until Barabási rediscovered the results under its current name (BA Model). According to this process, a page with many in-links will attract more in-links than a regular page. This generates a power-law but the resulting graph differs from the actual Web graph in other properties such as the presence of small tightly connected communities. More general models and network characteristics have been proposed and studied. For example, Pachon et al. (2018) proposed a variant of the rich get richer generative model which takes into account two different attachment rules: a preferential attachment mechanism and a uniform choice only for the most recent nodes.[27] For a review see the book by Dorogovtsev and Mendes.[citation needed] Some mechanisms such as super-linear preferential attachment and second neighbour attachment generate networks which are transiently scale-free, but deviate from a power law as networks grow large.[7][8]
A somewhat different generative model for Web links has been suggested by Pennock et al. (2002). They examined communities with interests in a specific topic such as the home pages of universities, public companies, newspapers or scientists, and discarded the major hubs of the Web. In this case, the distribution of links was no longer a power law but resembled a normal distribution. Based on these observations, the authors proposed a generative model that mixes preferential attachment with a baseline probability of gaining a link.
Another generative model is the copy model studied by Kumar et al.[28] (2000), in which new nodes choose an existent node at random and copy a fraction of the links of the existent node. This also generates a power law.
There are two major components that explain the emergence of the power-law distribution in the Barabási–Albert model: the growth and the preferential attachment.[29] By "growth" is meant a growth process where, over an extended period of time, new nodes join an already existing system, a network (like the World Wide Web which has grown by billions of web pages over 10 years). Finally, by "preferential attachment" is meant that new nodes prefer to connect to nodes that already have a high number of links with others. Thus, there is a higher probability that more and more nodes will link themselves to that one which has already many links, leading this node to a hub in-fine.[9] Depending on the network, the hubs might either be assortative or disassortative. Assortativity would be found in social networks in which well-connected/famous people would tend to know better each other. Disassortativity would be found in technological (Internet, World Wide Web) and biological (protein interaction, metabolism) networks.[29]
However, the growth of the networks (adding new nodes) is not a necessary condition for creating a scale-free network (see Dangalchev[30]). One possibility (Caldarelli et al. 2002) is to consider the structure as static and draw a link between vertices according to a particular property of the two vertices involved. Once specified the statistical distribution for these vertex properties (fitnesses), it turns out that in some circumstances also static networks develop scale-free properties.
Generalized scale-free model[edit]
There has been a burst of activity in the modeling of scale-free complex networks. The recipe of Barabási and Albert[31] has been followed by several variations and generalizations[32][33][34][35][27] and the revamping of previous mathematical works.[36]
In today's terms, if a complex network has a power-law distribution of any of its metrics, it's generally considered a scale-free network. Similarly, any model with this feature is called a scale-free model.[17]
Features[edit]
Many real networks are (approximately) scale-free and hence require scale-free models to describe them. In Price's scheme, there are two ingredients needed to build up a scale-free model:
1. Adding or removing nodes. Usually we concentrate on growing the network, i.e. adding nodes.
2. Preferential attachment: The probability that new nodes will be connected to the "old" node.
Note that some models (see Dangalchev[30] and Fitness model below) can work also statically, without changing the number of nodes. It should also be kept in mind that the fact that "preferential attachment" models give rise to scale-free networks does not prove that this is the mechanism underlying the evolution of real-world scale-free networks, as there might exist different mechanisms at work in real-world systems that nevertheless give rise to scaling.
Examples[edit]
There have been several attempts to generate scale-free network properties. Here are some examples:
The Barabási–Albert model[edit]
The Barabási–Albert model, an undirected version of Price's model has a linear preferential attachment and adds one new node at every time step.
(Note, another general feature of in real networks is that , i.e. there is a nonzero probability that a new node attaches to an isolated node. Thus in general has the form , where is the initial attractiveness of the node.)
Two-level network model[edit]
Dangalchev (see [30]) builds a 2-L model by considering the importance of each of the neighbours of a target node in preferential attachment. The attractiveness of a node in the 2-L model depends not only on the number of nodes linked to it but also on the number of links in each of these nodes.
where C is a coefficient between 0 and 1.
A variant of the 2-L model, the k2 model, where first and second neighbour nodes contribute equally to a target node's attractiveness, demonstrates the emergence of transient scale-free networks.[8] In the k2 model, the degree distribution appears approximately scale-free as long as the network is relatively small, but significant deviations from the scale-free regime emerge as the network grows larger. This results in the relative attractiveness of nodes with different degrees changing over time, a feature also observed in real networks.
Mediation-driven attachment (MDA) model[edit]
In the mediation-driven attachment (MDA) model, a new node coming with edges picks an existing connected node at random and then connects itself, not with that one, but with of its neighbors, also chosen at random. The probability that the node of the existing node picked is
The factor is the inverse of the harmonic mean (IHM) of degrees of the neighbors of a node . Extensive numerical investigation suggest that for approximately the mean IHM value in the large limit becomes a constant which means . It implies that the higher the links (degree) a node has, the higher its chance of gaining more links since they can be reached in a larger number of ways through mediators which essentially embodies the intuitive idea of rich get richer mechanism (or the preferential attachment rule of the Barabasi–Albert model). Therefore, the MDA network can be seen to follow the PA rule but in disguise.[37]
However, for it describes the winner takes it all mechanism as we find that almost of the total nodes has degree one and one is super-rich in degree. As value increases the disparity between the super rich and poor decreases and as we find a transition from rich get super richer to rich get richer mechanism.
Non-linear preferential attachment[edit]
The Barabási–Albert model assumes that the probability that a node attaches to node is proportional to the degree of node . This assumption involves two hypotheses: first, that depends on , in contrast to random graphs in which , and second, that the functional form of is linear in .
In non-linear preferential attachment, the form of is not linear, and recent studies have demonstrated that the degree distribution depends strongly on the shape of the function
Krapivsky, Redner, and Leyvraz[34] demonstrate that the scale-free nature of the network is destroyed for nonlinear preferential attachment. The only case in which the topology of the network is scale free is that in which the preferential attachment is asymptotically linear, i.e. as . In this case the rate equation leads to
This way the exponent of the degree distribution can be tuned to any value between 2 and .[clarification needed]
Hierarchical network model[edit]
Hierarchical network models are, by design, scale free and have high clustering of nodes.[38]
The iterative construction leads to a hierarchical network. Starting from a fully connected cluster of five nodes, we create four identical replicas connecting the peripheral nodes of each cluster to the central node of the original cluster. From this, we get a network of 25 nodes (N = 25). Repeating the same process, we can create four more replicas of the original cluster – the four peripheral nodes of each one connect to the central node of the nodes created in the first step. This gives N = 125, and the process can continue indefinitely.
Fitness model[edit]
The idea is that the link between two vertices is assigned not randomly with a probability p equal for all the couple of vertices. Rather, for every vertex j there is an intrinsic fitness xj and a link between vertex i and j is created with a probability .[39] In the case of World Trade Web it is possible to reconstruct all the properties by using as fitnesses of the country their GDP, and taking
Hyperbolic geometric graphs[edit]
Assuming that a network has an underlying hyperbolic geometry, one can use the framework of spatial networks to generate scale-free degree distributions. This heterogeneous degree distribution then simply reflects the negative curvature and metric properties of the underlying hyperbolic geometry.[41]
Edge dual transformation to generate scale free graphs with desired properties[edit]
Starting with scale free graphs with low degree correlation and clustering coefficient, one can generate new graphs with much higher degree correlations and clustering coefficients by applying edge-dual transformation.[19]
Uniform-preferential-attachment model (UPA model)[edit]
UPA model is a variant of the preferential attachment model (proposed by Pachon et al.) which takes into account two different attachment rules: a preferential attachment mechanism (with probability 1−p) that stresses the rich get richer system, and a uniform choice (with probability p) for the most recent nodes. This modification is interesting to study the robustness of the scale-free behavior of the degree distribution. It is proved analytically that the asymptotically power-law degree distribution is preserved.[27]
Scale-free ideal networks[edit]
In the context of network theory a scale-free ideal network is a random network with a degree distribution following the scale-free ideal gas density distribution. These networks are able to reproduce city-size distributions and electoral results by unraveling the size distribution of social groups with information theory on complex networks when a competitive cluster growth process is applied to the network.[42][43] In models of scale-free ideal networks it is possible to demonstrate that Dunbar's number is the cause of the phenomenon known as the 'six degrees of separation'.
Novel characteristics[edit]
For a scale-free network with nodes and power-law exponent , the induced subgraph constructed by vertices with degrees larger than is a scale-free network with , almost surely.[44]
Estimating the power law exponent[edit]
Estimating the power-law exponent of a scale-free network is typically done by using the maximum likelihood estimation with the degrees of a few uniformly sampled nodes.[3] However, since uniform sampling does not obtain enough samples from the important heavy-tail of the power law degree distribution, this method can yield a large bias and a variance. It has been recently proposed to sample random friends (i.e., random ends of random links) who are more likely come from the tail of the degree distribution as a result of the friendship paradox.[45][46] Theoretically, maximum likelihood estimation with random friends lead to a smaller bias and a smaller variance compared to classical approach based on uniform sampling.[46]
See also[edit]
- Random graph – Graph generated by a random process
- Erdős–Rényi model – Two closely related models for generating random graphs
- Non-linear preferential attachment
- Bose–Einstein condensation (network theory) – model in network science
- Scale invariance – Features that do not change if length or energy scales are multiplied by a common factor
- Complex network – Network with non-trivial topological features
- Webgraph – Graph of connected web pages
- Barabási–Albert model – Scale-free network generation algorithm
- Bianconi–Barabási model – model in network science
References[edit]
- ^ Onnela, J.-P.; Saramaki, J.; Hyvonen, J.; Szabo, G.; Lazer, D.; Kaski, K.; Kertesz, J.; Barabasi, A. -L. (2007). "Structure and tie strengths in mobile communication networks". Proceedings of the National Academy of Sciences. 104 (18): 7332–7336. arXiv:physics/0610104. Bibcode:2007PNAS..104.7332O. doi:10.1073/pnas.0610245104. PMC 1863470. PMID 17456605.
- ^ Choromański, K.; Matuszak, M.; MiȩKisz, J. (2013). "Scale-Free Graph with Preferential Attachment and Evolving Internal Vertex Structure". Journal of Statistical Physics. 151 (6): 1175–1183. Bibcode:2013JSP...151.1175C. doi:10.1007/s10955-013-0749-1.
- ^ a b c Clauset, Aaron; Cosma Rohilla Shalizi; M. E. J Newman (2009). "Power-law distributions in empirical data". SIAM Review. 51 (4): 661–703. arXiv:0706.1062. Bibcode:2009SIAMR..51..661C. doi:10.1137/070710111. S2CID 9155618.
- ^ Broido, Anna; Aaron Clauset (2019-03-04). "Scale-free networks are rare". Nature Communications. 10 (1): 1017. arXiv:1801.03400. Bibcode:2019NatCo..10.1017B. doi:10.1038/s41467-019-08746-5. PMC 6399239. PMID 30833554.
- ^ Holme, Petter (December 2019). "Rare and everywhere: Perspectives on scale-free networks". Nature Communications. 10 (1): 1016. Bibcode:2019NatCo..10.1016H. doi:10.1038/s41467-019-09038-8. PMC 6399274. PMID 30833568.
- ^ Stumpf, M. P. H.; Porter, M. A. (10 February 2012). "Critical Truths About Power Laws". Science. 335 (6069): 665–666. Bibcode:2012Sci...335..665S. doi:10.1126/science.1216142. PMID 22323807. S2CID 206538568.
- ^ a b Krapivsky, Paul; Krioukov, Dmitri (21 August 2008). "Scale-free networks as preasymptotic regimes of superlinear preferential attachment". Physical Review E. 78 (2): 026114. arXiv:0804.1366. Bibcode:2008PhRvE..78b6114K. doi:10.1103/PhysRevE.78.026114. PMID 18850904. S2CID 14292535.
- ^ a b c Falkenberg, Max; Lee, Jong-Hyeok; Amano, Shun-ichi; Ogawa, Ken-ichiro; Yano, Kazuo; Miyake, Yoshihiro; Evans, Tim S.; Christensen, Kim (18 June 2020). "Identifying time dependence in network growth". Physical Review Research. 2 (2): 023352. arXiv:2001.09118. Bibcode:2020PhRvR...2b3352F. doi:10.1103/PhysRevResearch.2.023352.
- ^ a b c Barabási, Albert-László; Albert, Réka. (October 15, 1999). "Emergence of scaling in random networks". Science. 286 (5439): 509–512. arXiv:cond-mat/9910332. Bibcode:1999Sci...286..509B. doi:10.1126/science.286.5439.509. MR 2091634. PMID 10521342. S2CID 524106.
- ^ Among the seven examples studied by Amaral et al, six of them where single-scale and only example iii, the movie-actor network had a power law regime followed by a sharp cutoff. None of Amaral et al's examples obeyed the power law regime for large k, i.e. none of these seven examples were shown to be scale-free. See especially the beginning of the discussion section of Amaral LAN, Scala A, Barthelemy M, Stanley HE (2000). "Classes of small-world networks". PNAS. 97 (21): 11149–52. arXiv:cond-mat/0001458. Bibcode:2000PNAS...9711149A. doi:10.1073/pnas.200327197. PMC 17168. PMID 11005838.
- ^ Dorogovtsev, S.; Mendes, J.; Samukhin, A. (2000). "Structure of Growing Networks with Preferential Linking". Physical Review Letters. 85 (21): 4633–4636. arXiv:cond-mat/0004434. Bibcode:2000PhRvL..85.4633D. doi:10.1103/PhysRevLett.85.4633. PMID 11082614. S2CID 118876189.
- ^ Bollobás, B.; Riordan, O.; Spencer, J.; Tusnády, G. (2001). "The degree sequence of a scale-free random graph process". Random Structures and Algorithms. 18 (3): 279–290. doi:10.1002/rsa.1009. MR 1824277. S2CID 1486779.
- ^ Dorogovtsev, S. N.; Mendes, J. F. F. (2002). "Evolution of networks". Advances in Physics. 51 (4): 1079–1187. arXiv:cond-mat/0106144. Bibcode:2002AdPhy..51.1079D. doi:10.1080/00018730110112519. S2CID 429546.
- ^ Willinger, Walter; David Alderson; John C. Doyle (May 2009). "Mathematics and the Internet: A Source of Enormous Confusion and Great Potential" (PDF). Notices of the AMS. 56 (5). American Mathematical Society: 586–599. Archived (PDF) from the original on 2011-05-15. Retrieved 2011-02-03.
- ^ Itzykson, Claude; Drouffe, Jean-Michel (1989). Statistical Field Theory: Volume 1, From Brownian Motion to Renormalization and Lattice Gauge Theory (1st ed.). New York: Cambridge University Press. ISBN 978-0-521-34058-8.
- ^ Itzykson, Claude; Drouffe, Jean-Michel (1989). Statistical Field Theory: Volume 2, Strong Coupling, Monte Carlo Methods, Conformal Field Theory and Random Systems (1st ed.). New York: Cambridge University Press. ISBN 978-0-521-37012-7.
- ^ a b Meng, Xiangyi; Zhou, Bin (2023). "Scale-Free Networks beyond Power-Law Degree Distribution". Chaos, Solitons & Fractals. 176: 114173. arXiv:2310.08110. Bibcode:2023CSF...17614173M. doi:10.1016/j.chaos.2023.114173. S2CID 263909425.
- ^ Tanaka, Reiko (2005). "Scale-Rich Metabolic Networks". Phys. Rev. Lett. 94 (16): 168101. Bibcode:2005PhRvL..94p8101T. doi:10.1103/PhysRevLett.94.168101. PMID 15904266.
- ^ a b Ramezanpour, A.; Karimipour, V.; Mashaghi, A. (2003). "Generating correlated networks from uncorrelated ones". Phys. Rev. E. 67 (4): 046107. arXiv:cond-mat/0212469. Bibcode:2003PhRvE..67d6107R. doi:10.1103/PhysRevE.67.046107. PMID 12786436. S2CID 33054818.
- ^ De Masi, Giulia; et al. (2006). "Fitness model for the Italian interbank money market". Physical Review E. 74 (6): 066112. arXiv:physics/0610108. Bibcode:2006PhRvE..74f6112D. doi:10.1103/PhysRevE.74.066112. PMID 17280126. S2CID 30814484.
- ^ Soramäki, Kimmo; et al. (2007). "The topology of interbank payment flows". Physica A: Statistical Mechanics and Its Applications. 379 (1): 317–333. Bibcode:2007PhyA..379..317S. doi:10.1016/j.physa.2006.11.093. hdl:10419/60649.
- ^ Steyvers, Mark; Joshua B. Tenenbaum (2005). "The Large-Scale Structure of Semantic Networks: Statistical Analyses and a Model of Semantic Growth". Cognitive Science. 29 (1): 41–78. arXiv:cond-mat/0110012. doi:10.1207/s15516709cog2901_3. PMID 21702767. S2CID 6000627.
- ^ Fratini, Michela; Poccia, Nicola; Ricci, Alessandro; Campi, Gaetano; Burghammer, Manfred; Aeppli, Gabriel; Bianconi, Antonio (2010). "Scale-free structural organization of oxygen interstitials in La2CuO4+y". Nature. 466 (7308): 841–4. arXiv:1008.2015. Bibcode:2010Natur.466..841F. doi:10.1038/nature09260. PMID 20703301. S2CID 4405620.
- ^ Poccia, Nicola; Ricci, Alessandro; Campi, Gaetano; Fratini, Michela; Puri, Alessandro; Di Gioacchino, Daniele; Marcelli, Augusto; Reynolds, Michael; Burghammer, Manfred; Saini, Naurang L.; Aeppli, Gabriel; Bianconi, Antonio (2012). "Optimum inhomogeneity of local lattice distortions in La2CuO4+y". PNAS. 109 (39): 15685–15690. arXiv:1208.0101. Bibcode:2012PNAS..10915685P. doi:10.1073/pnas.1208492109. PMC 3465392. PMID 22961255.
- ^ Hassan, M. K.; Hassan, M. Z.; Pavel, N. I. (2010). "Scale-free network topology and multifractality in a weighted planar stochastic lattice". New Journal of Physics. 12 (9): 093045. arXiv:1008.4994. Bibcode:2010NJPh...12i3045H. doi:10.1088/1367-2630/12/9/093045.
- ^ Hassan, M. K.; Hassan, M. Z.; Pavel, N. I. (2010). "Scale-free coordination number disorder and multifractal size disorder in weighted planar stochastic lattice". J. Phys.: Conf. Ser. 297: 01.
- ^ a b c Pachon, Angelica; Sacerdote, Laura; Yang, Shuyi (2018). "Scale-free behavior of networks with the copresence of preferential and uniform attachment rules". Physica D: Nonlinear Phenomena. 371: 1–12. arXiv:1704.08597. Bibcode:2018PhyD..371....1P. doi:10.1016/j.physd.2018.01.005. S2CID 119320331.
- ^ Kumar, Ravi; Raghavan, Prabhakar (2000). Stochastic Models for the Web Graph (PDF). Foundations of Computer Science, 41st Annual Symposium on. pp. 57–65. doi:10.1109/SFCS.2000.892065. Archived (PDF) from the original on 2016-03-03. Retrieved 2016-02-10.
- ^ a b Barabási, Albert-László; Zoltán N., Oltvai. (2004). "Network biology: understanding the cell's functional organization". Nature Reviews Genetics. 5 (2): 101–113. doi:10.1038/nrg1272. PMID 14735121. S2CID 10950726.
- ^ a b c Dangalchev, Chavdar (July 2004). "Generation models for scale-free networks". Physica A: Statistical Mechanics and Its Applications. 338 (3–4): 659–671. Bibcode:2004PhyA..338..659D. doi:10.1016/j.physa.2004.01.056.
- ^ Barabási, A.-L. and R. Albert, Science 286, 509 (1999).
- ^ R. Albert, and A.L. Barabási, Phys. Rev. Lett. 85, 5234(2000).
- ^ S. N. Dorogovtsev, J. F. F. Mendes, and A. N. Samukhim, cond-mat/0011115.
- ^ a b P.L. Krapivsky, S. Redner, and F. Leyvraz, Phys. Rev. Lett. 85, 4629 (2000).
- ^ B. Tadic, Physica A 293, 273(2001).
- ^ S. Bomholdt and H. Ebel, cond-mat/0008465; H.A. Simon, Bimetrika 42, 425(1955).
- ^ Hassan, M. K.; Islam, Liana; Arefinul Haque, Syed (2017). "Degree distribution, rank-size distribution, and leadership persistence in mediation-driven attachment networks". Physica A. 469: 23–30. arXiv:1411.3444. Bibcode:2017PhyA..469...23H. doi:10.1016/j.physa.2016.11.001. S2CID 51976352.
- ^ Ravasz, E.; Barabási (2003). "Hierarchical organization in complex networks". Phys. Rev. E. 67 (2): 026112. arXiv:cond-mat/0206130. Bibcode:2003PhRvE..67b6112R. doi:10.1103/physreve.67.026112. PMID 12636753. S2CID 17777155.
- ^ Caldarelli, G.; et al. (2002). "Scale-free networks from varying vertex intrinsic fitness" (PDF). Phys. Rev. Lett. 89 (25): 258702. Bibcode:2002PhRvL..89y8702C. doi:10.1103/physrevlett.89.258702. PMID 12484927.
- ^ Garlaschelli, D.; et al. (2004). "Fitness-Dependent Topological Properties of the World Trade Web". Phys. Rev. Lett. 93 (18): 188701. arXiv:cond-mat/0403051. Bibcode:2004PhRvL..93r8701G. doi:10.1103/physrevlett.93.188701. PMID 15525215. S2CID 16367275.
- ^ Krioukov, Dmitri; Papadopoulos, Fragkiskos; Kitsak, Maksim; Vahdat, Amin; Boguñá, Marián (2010). "Hyperbolic geometry of complex networks". Physical Review E. 82 (3): 036106. arXiv:1006.5169. Bibcode:2010PhRvE..82c6106K. doi:10.1103/PhysRevE.82.036106. PMID 21230138. S2CID 6451908.
- ^ A. Hernando; D. Villuendas; C. Vesperinas; M. Abad; A. Plastino (2009). "Unravelling the size distribution of social groups with information theory on complex networks". arXiv:0905.3704 [physics.soc-ph]., submitted to European Physical Journal B
- ^ André A. Moreira; Demétrius R. Paula; Raimundo N. Costa Filho; José S. Andrade, Jr. (2006). "Competitive cluster growth in complex networks". Physical Review E. 73 (6): 065101. arXiv:cond-mat/0603272. Bibcode:2006PhRvE..73f5101M. doi:10.1103/PhysRevE.73.065101. PMID 16906890. S2CID 45651735.
- ^ Heydari, H.; Taheri, S.M.; Kaveh, K. (2018). "Distributed Maximal Independent Set on Scale-Free Networks". arXiv:1804.02513 [cs.DC].
- ^ Eom, Young-Ho; Jo, Hang-Hyun (2015-05-11). "Tail-scope: Using friends to estimate heavy tails of degree distributions in large-scale complex networks". Scientific Reports. 5 (1): 9752. arXiv:1411.6871. Bibcode:2015NatSR...5E9752E. doi:10.1038/srep09752. ISSN 2045-2322. PMC 4426729. PMID 25959097.
- ^ a b Nettasinghe, Buddhika; Krishnamurthy, Vikram (2021-05-19). "Maximum Likelihood Estimation of Power-law Degree Distributions via Friendship Paradox-based Sampling". ACM Transactions on Knowledge Discovery from Data. 15 (6): 1–28. arXiv:1908.00310. doi:10.1145/3451166. ISSN 1556-4681.
Further reading[edit]
- Albert R.; Barabási A.-L. (2002). "Statistical mechanics of complex networks". Rev. Mod. Phys. 74 (1): 47–97. arXiv:cond-mat/0106096. Bibcode:2002RvMP...74...47A. doi:10.1103/RevModPhys.74.47. S2CID 60545.
- Amaral LAN, Scala A, Barthelemy M, Stanley HE (2000). "Classes of small-world networks". PNAS. 97 (21): 11149–52. arXiv:cond-mat/0001458. Bibcode:2000PNAS...9711149A. doi:10.1073/pnas.200327197. PMC 17168. PMID 11005838.
- Barabási, Albert-László (2004). Linked: How Everything is Connected to Everything Else. Perseus Pub. ISBN 0-452-28439-2.
- Barabási, Albert-László; Bonabeau, Eric (May 2003). "Scale-Free Networks" (PDF). Scientific American. 288 (5): 50–9. Bibcode:2003SciAm.288e..60B. doi:10.1038/scientificamerican0503-60. PMID 12701331.
- Dan Braha; Yaneer Bar-Yam (2004). "Topology of Large-Scale Engineering Problem-Solving Networks" (PDF). Phys. Rev. E. 69 (1): 016113. Bibcode:2004PhRvE..69a6113B. doi:10.1103/PhysRevE.69.016113. PMID 14995673. S2CID 1001176.
- Caldarelli G. "Scale-Free Networks" Oxford University Press, Oxford (2007).
- Caldarelli G.; Capocci A.; De Los Rios P.; Muñoz M.A. (2002). "Scale-free networks from varying vertex intrinsic fitness". Physical Review Letters. 89 (25): 258702. arXiv:cond-mat/0207366. Bibcode:2002PhRvL..89y8702C. doi:10.1103/PhysRevLett.89.258702. PMID 12484927.
- Dangalchev, Ch. (2004). "Generation models for scale-free networks". Physica A. 338 (3–4): 659–671. Bibcode:2004PhyA..338..659D. doi:10.1016/j.physa.2004.01.056.
- Dorogovtsev, S.N.; Mendes, J.F.F.; Samukhin, A.N. (2000). "Structure of Growing Networks: Exact Solution of the Barabási—Albert's Model". Phys. Rev. Lett. 85 (21): 4633–6. arXiv:cond-mat/0004434. Bibcode:2000PhRvL..85.4633D. doi:10.1103/PhysRevLett.85.4633. PMID 11082614. S2CID 118876189.
- Dorogovtsev, S.N.; Mendes, J.F.F. (2003). Evolution of Networks: from biological networks to the Internet and WWW. Oxford University Press. ISBN 0-19-851590-1.
- Dorogovtsev, S.N.; Goltsev A.V.; Mendes, J.F.F. (2008). "Critical phenomena in complex networks". Rev. Mod. Phys. 80 (4): 1275–1335. arXiv:0705.0010. Bibcode:2008RvMP...80.1275D. doi:10.1103/RevModPhys.80.1275. S2CID 3174463.
- Dorogovtsev, S.N.; Mendes, J.F.F. (2002). "Evolution of networks". Advances in Physics. 51 (4): 1079–1187. arXiv:cond-mat/0106144. Bibcode:2002AdPhy..51.1079D. doi:10.1080/00018730110112519. S2CID 429546.
- Erdős, P.; Rényi, A. (1960). On the Evolution of Random Graphs (PDF). Vol. 5. Publication of the Mathematical Institute of the Hungarian Academy of Science. pp. 17–61.
- Faloutsos, M.; Faloutsos, P.; Faloutsos, C. (1999). "On power-law relationships of the internet topology". Comp. Comm. Rev. 29 (4): 251–262. doi:10.1145/316194.316229.
- Li, L.; Alderson, D.; Tanaka, R.; Doyle, J.C.; Willinger, W. (2005). "Towards a Theory of Scale-Free Graphs: Definition, Properties, and Implications (Extended Version)". arXiv:cond-mat/0501169.
- Kumar, R.; Raghavan, P.; Rajagopalan, S.; Sivakumar, D.; Tomkins, A.; Upfal, E. (2000). "Stochastic models for the web graph" (PDF). Proceedings of the 41st Annual Symposium on Foundations of Computer Science (FOCS). Redondo Beach, CA: IEEE CS Press. pp. 57–65.
- Matlis, Jan (November 4, 2002). "Scale-Free Networks".
- Newman, Mark E.J. (2003). "The structure and function of complex networks". SIAM Review. 45 (2): 167–256. arXiv:cond-mat/0303516. Bibcode:2003SIAMR..45..167N. doi:10.1137/S003614450342480. S2CID 221278130.
- Pastor-Satorras, R.; Vespignani, A. (2004). Evolution and Structure of the Internet: A Statistical Physics Approach. Cambridge University Press. ISBN 0-521-82698-5.
- Pennock, D.M.; Flake, G.W.; Lawrence, S.; Glover, E.J.; Giles, C.L. (2002). "Winners don't take all: Characterizing the competition for links on the web". PNAS. 99 (8): 5207–11. Bibcode:2002PNAS...99.5207P. doi:10.1073/pnas.032085699. PMC 122747. PMID 16578867.
- Robb, John. Scale-Free Networks and Terrorism, 2004.
- Keller, E.F. (2005). "Revisiting "scale-free" networks". BioEssays. 27 (10): 1060–8. doi:10.1002/bies.20294. PMID 16163729. Archived from the original on 2011-08-13.
- Onody, R.N.; de Castro, P.A. (2004). "Complex Network Study of Brazilian Soccer Player". Phys. Rev. E. 70 (3): 037103. arXiv:cond-mat/0409609. Bibcode:2004PhRvE..70c7103O. doi:10.1103/PhysRevE.70.037103. PMID 15524675. S2CID 31653489.
- Kasthurirathna, D.; Piraveenan, M. (2015). "Complex Network Study of Brazilian Soccer Player". Sci. Rep. In Press.










































