Negative refraction: Difference between revisions
Reverted 2 good faith edits by 117.197.22.250 using STiki |
Typo. Changed 'principle' to 'principal'. |
||
| Line 26: | Line 26: | ||
==Refraction== |
==Refraction== |
||
The |
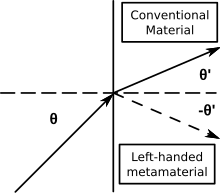
The principal symptom of negative refraction is just that – light rays are |
||
refracted on the ''same'' side of the normal on entering the material, as indicated in the diagram, and by a suitably general form of [[Snell's law]]. |
refracted on the ''same'' side of the normal on entering the material, as indicated in the diagram, and by a suitably general form of [[Snell's law]]. |
||
Revision as of 13:28, 13 December 2016
Negative refraction is the name for an electromagnetic phenomenon where light rays are refracted at an interface in the reverse sense to that normally expected. Such an effect can be obtained using a metamaterial which has been designed to achieve a negative value for both (electric) permittivity ε and (magnetic) permeability μ, as in such cases the material can be assigned a negative refractive index. Such materials are sometimes called "double negative" materials.
Negative refraction occurs at interfaces between materials at which one has an ordinary positive phase velocity (i.e. a positive refractive index), and the other has the more exotic negative phase velocity (a negative refractive index).
Negative phase velocity
Negative phase velocity (NPV) is a property of light propagation in a medium. There are different definitions of NPV, the most common being Veselago's original proposal [1] of opposition of wavevector and (Abraham) Poynting vector, i.e. E×H; other common choices are opposition of wavevector to group velocity, or to energy velocity. The use of "phase velocity" in the naming convention, as opposed to the perhaps more appropriate "wave vector", follows since phase velocity has the same sign as the wavevector.
A typical criterion used to determine Veselago NPV is that the dot product of the Poynting vector and wavevector is negative (i.e. that ); however this definition is not covariant. Whilst this restriction is rarely of practical significance, the criterion has nevertheless been generalized into a covariant form.[2] For plane waves propagating in a Veselago NPV medium, the electric field, magnetic field and wave vector follow a left-hand rule, rather than the usual right-hand rule. This gives rise to the name "left-handed (meta)materials". However, the terms left-handed and right-handed can also arise in the study of chiral media, so this terminology is best avoided.
Negative refractive index
We can choose to avoid directly considering the Poynting vector and wavevector or a propagating light field, and consider instead the response of the materials directly: that is, we consider what values of permittivity ε and permeability µ result in negative phase velocity (NPV). Since both ε and µ are in general complex, their imaginary parts do not have to be negative for a passive (i.e. lossy) material to display negative refraction. The most general Veselago criterion applying to ε and µ is that of Depine and Lakhtakia,[3] although other less general forms exist.[4] The Depine-Lakhtakia criterion for negative phase velocity is
where are the real valued parts of ε and µ, respectively. However, negative refraction (negative refractive index) and negative phase velocity can be distinct from each other, even in passive materials,[5] but also in active materials.[6]
Typically, the refractive index n is determined using , where by convention the positive square root is chosen for n. However, in NPV materials, we reverse that convention and pick the negative sign to mimic the fact that the wavevector (and hence phase velocity) are likewise reversed. Strictly speaking, the refractive index is a derived quantity telling us how the wavevector is related to the optical frequency and propagation direction of the light, thus the sign of n must be chosen to match the physical situation.
Refraction
The principal symptom of negative refraction is just that – light rays are refracted on the same side of the normal on entering the material, as indicated in the diagram, and by a suitably general form of Snell's law.
References
- ^ V. G. Veselago (1968 (Russian text 1967)). "The electrodynamics of substances with simultaneously negative values of ε and μ". Sov. Phys. Usp. 10 (4): 509–14. Bibcode:1968SvPhU..10..509V. doi:10.1070/PU1968v010n04ABEH003699.
{{cite journal}}: Check date values in:|year=(help)CS1 maint: year (link) - ^ M. W. McCall (2008). "A Covariant Theory of Negative Phase Velocity Propagation". Metamaterials. 2: 92. Bibcode:2008MetaM...2...92M. doi:10.1016/j.metmat.2008.05.001.
- ^ R. A. Depine and A. Lakhtakia (2004). "A new condition to identify isotropic dielectric-magnetic materials displaying negative phase velocity". Microwave and Optical Technology Letters. 41: 315. doi:10.1002/mop.20127.
- ^ P. Kinsler and M. W. McCall (2008). "Criteria for negative refraction in active and passive media". Microwave and Optical Technology Letters. 50: 1804. doi:10.1002/mop.23489.
- ^ T. G. Mackay and A. Lakhtakia (2009). "Negative refraction, negative phase velocity, and counterposition in bianisotropic materials and metamaterials". Physical Review B. 79: 235121. Bibcode:2009PhRvB..79w5121M. doi:10.1103/PhysRevB.79.235121.
- ^ J. Skaar (2006). "On resolving the refractive index and the wave vector". Optics Letters. 31: 3372. arXiv:physics/0607104. Bibcode:2006OptL...31.3372S. doi:10.1364/OL.31.003372.
See also
- Acoustic metamaterials
- Metamaterial
- Negative index metamaterials
- Metamaterial antennas
- Multiple-prism dispersion theory
- Perfect lens
- Photonic metamaterials
- Photonic crystal
- Seismic metamaterials
- Split-ring resonator
- Tunable metamaterials




