Hypotrochoid

The red curve is a hypotrochoid drawn as the smaller black circle rolls around inside the larger blue circle (parameters are R = 5, r = 3, d = 5).

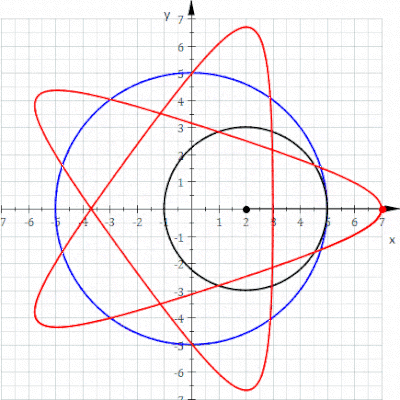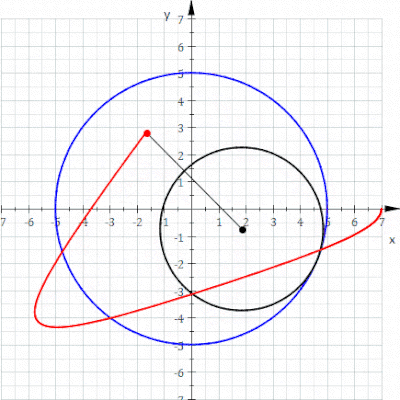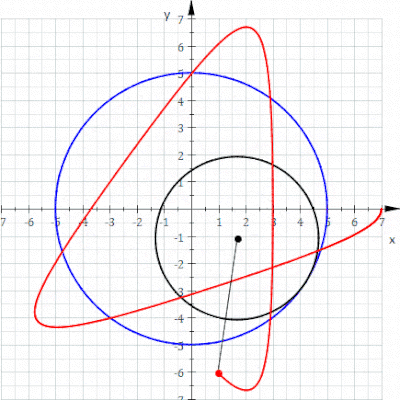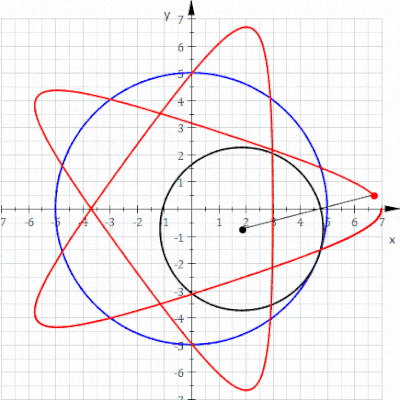
A hypotrochoid is a roulette traced by a point attached to a circle of radius r rolling around the inside of a fixed circle of radius R, where the point is a distance d from the center of the interior circle.

The parametric equations for a hypotrochoid are:

$x(\theta )=(R-r)\cos \theta +d\cos \left({R-r \over r}\theta \right)$

$y(\theta )=(R-r)\sin \theta -d\sin \left({R-r \over r}\theta \right).$

Where $\theta$ is the angle formed by the horizontal and the center of the rolling circle (these are not polar equations because $\theta$ is not the polar angle). When measured in radian, $\theta$ takes value from $0$ to $2*\pi *{\frac {LCM(r,R)}{r}}$where LCM is least common multiple.

Special cases include the hypocycloid with d = r and the ellipse with R = 2r. (see Tusi couple)

The ellipse (drawn in red) may be expressed as a special case of the hypotrochoid, with R = 2r (Tusi couple); here R = 10, r = 5, d = 1.

The classic Spirograph toy traces out hypotrochoid and epitrochoid curves.

See also

• Cycloid
• Cyclogon
• Epicycloid
• Rosetta (orbit)
• Apsidal precession

External links

• Weisstein, Eric W. "Hypotrochoid". MathWorld.
• Flash Animation of Hypocycloid
• Hypotrochoid from Visual Dictionary of Special Plane Curves, Xah Lee
• Interactive hypotrochoide animation
• O'Connor, John J.; Robertson, Edmund F., "Hypotrochoid", MacTutor History of Mathematics Archive, University of St Andrews