Jump to content

Amphidromic point

From Wikipedia, the free encyclopedia

This is an old revision of this page, as edited by CommonsDelinker (talk | contribs) at 01:02, 25 May 2021 (Removing Sum_of_Kelvin_waves.gif; it has been deleted from Commons by JuTa because: No license since 14 May 2021.). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

Figure 1. The M2 tidal constituent, the amplitude indicated by color. The white lines are cotidal lines spaced at phase intervals of 30° (a bit over 1 hr).[1] The amphidromic points are the dark blue areas where the lines come together.
"Amphidrome" redirects here. For the former stadium in Houghton, Michigan, see Dee Stadium.

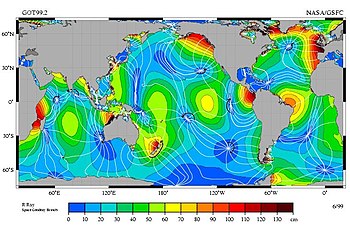
An amphidromic point, also called a tidal node, is a geographical location which has zero tidal amplitude for one harmonic constituent of the tide.[2] The tidal range (the peak-to-peak amplitude, or height difference between high tide and low tide) for that harmonic constituent increases with distance from this point.[3]

The term amphidromic point derives from the Greek words amphi (around) and dromos (running), referring to the rotary tides running around them.[4]

Amphidromic points occur because the Coriolis effect and interference within oceanic basins, seas and bays creates a wave pattern — called an amphidromic system — which rotates around the amphidromic point.[3][5] At the amphidromic points of the dominant tidal constituent, there is almost no vertical movement from tidal action. There can be tidal currents since the water levels on either side of the amphidromic point are not the same. A separate amphidromic system is created by each periodic tidal component.[6]

In most locations the "principal lunar semi-diurnal", known as M2, is the largest tidal constituent, with an amplitude of roughly half of the full tidal range. Having cotidal points means they reach high tide at the same time and low tide at the same time. In Figure 1, the low tide lags or leads by 1 hr 2 min from its neighboring lines. Where the lines meet are amphidromes, and the tide rotates around them; for example, along the Chilean coast, and from southern Mexico to Peru, the tide propagates southward, while from Baja California to Alaska the tide propagates northward.

Introduction

Tides play a key role in the dynamics of coastal regions and estuaries. Tide induced currents and changes in water level cause morphological changes in coastal areas[7][8][9]. Moreover, tides play an important role in coastal management[10][11]. Amphidromic points are certain locations in oceans and seas at which the amplitude of the tidal wave vanishes and around which the phase of the tide propagates. Furthermore, the amplitude of the tidal wave increases when moving farther away from an amphidromic point. As such, amphidromic points are crucial in understanding the tidal behaviour.

Formation of amphidromic points

Figure 2. Resonance between an incident and reflected wave and the resulting total wave. The nodes and the antinodes of the total wave are shown with their distance apart.

Tides are generated as a result of gravitational attraction by the sun and moon.[12] This gravitational attraction results in a tidal force that acts on the ocean.[12] The ocean reacts to this external forcing by generating, in particular relevant for describing tidal behaviour, Kelvin waves and Poincaré waves (also known as Sverdrup waves).[12] These tidal waves can be considered to be wide, relative to the Rossby radius of deformation (~3000 km in the open ocean[13]), and shallow, as the water depth (D, on average ~4 kilometre deep[14]) in the ocean is much smaller (i.e. D/λ <1/20) than the wavelength (λ) which is in the order of thousands of kilometres.[12][15]

In real oceans, the tides cannot endlessly propagate as progressive waves. The waves reflect due to changes in water depth (for example when entering shelf seas) and at coastal boundaries.[12] The result is a reflected wave that propagates in the opposite direction to the incident wave. The combination of the reflected wave and the incident wave is the total wave.[16] Due to resonance between the reflected and the incident wave, the amplitude of the total wave can either be suppressed or amplified.[12] The points at which the which the two waves amplify each other are known as antinodes and the points at which the two waves cancel each other out are known as nodes. Figure 2 shows a ¼λ resonator. The first node is located at ¼λ of the total wave, followed by the next node reoccurring ½λ farther at ¾λ.

A long, progressive wave travelling in a channel on a rotating earth behaves differently from a wave travelling along a non-rotating channel. Due to the Coriolis force, the water in the ocean is deflected towards the right in the northern hemisphere and conversely in the southern hemisphere.[12] This side-way component of the flow caused by the Coriolis force causes a build-up of water that results in a pressure gradient.[12] The resulting slope develops until it is equilibrium with the Coriolis force; resulting in geostrophic balance.[17] As a result this geostrophic balance, Kelvin waves (originally described by Lord Kelvin) and Poincaré waves are generated. The amplitude of a Kelvin wave is highest near the coast and, when considering a wave on the northern hemisphere, decreases to further away from its right-hand coastal boundary.[13] The propagation of Kelvin waves is always alongshore and its amplification falls off according to the Rossby radius of deformation[13]. In contrast, Poincaré waves are able to propagate both alongshore as a free wave with a propagating wave pattern and cross-shore as a trapped wave with a standing wave pattern.[18]

Infinitely long channel

Let us now make a simplified approximation of an ocean with boundaries at both sides of the channel (i.e. Atlantic Ocean and Pacific Ocean), in which there is incident and a reflective Kelvin wave as shown in Animation 1. The red coloured lines indicate high tide and the blue coloured lines indicate low tide. Furthermore, the vectors field below the basin in Animation 1 show the direction and the strength of the tidal current. The amplitude of the waves decreases further away from the coast and at certain points in the middle of the basin, the amplitude of the total wave becomes zero. Moreover, the phase of the tide seems to rotate around these points of zero amplitude. These points are called amphidromic points. The sense of rotation of the wave around the amphidromic point is in the direction of the Coriolis force; anticlockwise in the northern hemisphere and clockwise in the southern hemisphere.

Semi-enclosed basin

File:Summation of tidal waves in a semi-enclosed basin.gif
Animation 2. Summation of alongshore incident and reflected Kelvin waves and cross-shore Poincaré waves in a frictionless, semi-enclosed basin. Red coloured lines indicate high tide and blue coloured lines indicate low tide. The vector field shows the strength and the direction of the current. Courtesy of dr. ir. Pieter C. Roos, Water Engineering & Management, University of Twente.

Let us now consider a semi-enclosed basin, which can be viewed upon as a simplified approximation of, for example, the North Sea. Kelvin waves, though being the dominant tidal wave propagating in alongshore direction, are not able to propagate cross shore as they rely on the presence of vertical boundaries or the equator.[13] As such, the tidal waves observed cross-shore are predominantly Poincaré waves. The tides we observe in a semi-enclosed basin are therefore chiefly the summation of the incident Kelvin wave, reflected Kelvin wave and cross-shore standing Poincaré wave. An animation of the tidal amplitude, tidal currents and its amphidromic behaviour is shown in Animation 2.

Position of amphidromic points

In Figure 2, we saw that the first node of the total wave is located at ¼λ with reoccurring nodes at intervals of ½λ. In an idealized situation, amphidromic points can be found at the position of these nodes of the total tidal wave.[12] When neglecting friction, the position of the amphidromic points would be in the middle of the basin, as the initial amplitude and the amplitude decay of the incident wave and the reflected wave are equal.[12] This can be seen in Animations 1 and 2. However, tidal waves in the ocean are not only subject to friction from the seabed and from interaction with coastal boundaries, but also to varying water depth.[12][14] Firstly, the distance between amphidromic points is dependent on the water depth:[12]

(1)

Where g is the gravitational acceleration, D is the water depth and T is the period of the wave.

Locations with a more shallow water depth, have their amphidromic points closer to each other as the distance of the interval of the nodes decreases. Secondly, energy losses due to friction in shallow seas and coastal boundaries result in additional adjustments of the tidal pattern.[19] Tidal waves are not perfectly reflected, resulting in energy loss which causes a smaller reflected wave compared to the incoming wave.[12] Consequently, on the northern hemisphere, the amphidromic point will be displaced from the centre line of the channel towards the left of the direction of the incident wave.[12] The degree of displacement on the northern hemisphere for the first amphidrome is given by:[12]

(2)

Where γ is the displacement of the amphidrome from the centre of the channel (γ=0), g is the gravitational acceleration, D is the water depth, f is the Coriolis frequency and α is the ratio between amplitudes of the reflected wave and the incident wave. Because the reflected wave is smaller than the incident wave,[12] α will be smaller than 1 and lnα will be negative. Hence the amphidromic displacement γ is to the left of the incident wave on the northern hemisphere.

Furthermore, study has shown than there is a pattern of amphidrome movement related to spring-neap cycles in the Irish Sea.[19] The maximum displacement of the amphidrome from the centre coincides with spring tides, whereas the minimum occurs at neaps. During spring tides, more energy is absorbed from the tidal wave compared to neap tides. As a result, the reflection coefficient α is smaller and the displacement of the amphidromic point from the centre is larger. Similar amphidromic movement is expected in other seas where energy dissipation due to friction is high.[12]

It can occur that the amphidromic point moves inland of the coastal boundary.[19][20][21] In this case, the amplitude and the phase of the tidal wave will still rotate around an inland point, which is called a virtual or degenerate amphidrome.

Amphidromic points and sea level rise

The position of amphidromic points and their movement predominantly depends on the wavelength of the tidal wave and friction. As a result of enhanced greenhouse gas emissions, the oceans in the world are becoming subject to sea-level rise.[22][23] As the water depth increases, the wavelength of the tidal wave will increase, in accordance with Equation 1. Consequently the position of the amphidromic points located at ¼λ in semi-enclosed systems will move further away from the cross-shore coastal boundary. Furthermore, amphidromic points will move further away from each other as the interval of ½λ increases. This effect will be more pronounced in shallow seas and coastal regions, as the relative water depth increase due to sea-level rise will be larger, when compared to the open ocean. Moreover, the amount of sea-level rise differs per region.[24] Some regions will be subject to a higher rate of sea-level rise than other regions and nearby amphidromic points will be more susceptible to change location. Lastly, sea-level rise results in less bottom friction and therefore less energy dissipation.[25] This causes the amphidromic points to move further away from the coastal boundaries and more towards the centre its channel/basin.

In the M2 tidal constituent

Based on Figure 3, there are following clockwise and counterclockwise amphidromic points:

Figure 1. Amphidromic system of the M2 constituent in the North Sea. The light-blue lines are lines of equal tidal phase for the vertical tide (surface elevation) along such a line, and the amphidromic points are denoted by 1, 2 and 3.

Clockwise amphidromic points

Counterclockwise amphidromic points

See also

References and notes

  1. ^ Picture credit: R. Ray, TOPEX/Poseidon: Revealing Hidden Tidal Energy GSFC, NASA. Redistribute with credit to R. Ray, as well as NASA-GSFC, NASA-JPL, Scientific Visualization Studio, and Television Production NASA-TV/GSFC
  2. ^ Desplanque, Con; Mossman, David J. (1 January 2004). "Tides and their seminal impact on the geology, geography, history, and socio-economics of the Bay of Fundy, eastern Canada". Atlantic Geology. 40 (1). doi:10.4138/729.
  3. ^ a b "Tides in two easy pieces - Earth 540: Essentials of Oceanography for Educators". Retrieved 21 July 2016.
  4. ^ Cartwright, David Edgar (2000). Tides: A Scientific History. Cambridge University Press. p. 243. ISBN 978-0-521-79746-7.
  5. ^ http://www.salemstate.edu/~lhanson/gls214/gls214_tides.html
  6. ^ "Untitled Document". Retrieved 21 July 2016.
  7. ^ Ensign, Scott H.; Doyle, Martin W.; Piehler, Michael F. (2013-03-08). "The effect of tide on the hydrology and morphology of a freshwater river". Earth Surface Processes and Landforms. 38 (6): 655–660. doi:10.1002/esp.3392. ISSN 0197-9337.
  8. ^ Wang, Z.B; Jeuken, M.C.J.L; Gerritsen, H; de Vriend, H.J; Kornman, B.A (November 2002). "Morphology and asymmetry of the vertical tide in the Westerschelde estuary". Continental Shelf Research. 22 (17): 2599–2609. doi:10.1016/s0278-4343(02)00134-6. ISSN 0278-4343.
  9. ^ Masselink, Gerd (2021-03-05). "Sandy Beach Morphodynamics". Journal of Coastal Research. 37 (2). doi:10.2112/jcoastres-d-20a-00008.1. ISSN 0749-0208.
  10. ^ Platt, Rutherford H.; Beatley, Timothy; Brower, David J.; Schwab, Anna K. (October 1995). "An Introduction to Coastal Zone Management". Economic Geography. 71 (4): 440. doi:10.2307/144429. ISSN 0013-0095.
  11. ^ Pickering, M.D.; Horsburgh, K.J.; Blundell, J.R.; Hirschi, J.J.-M.; Nicholls, R.J.; Verlaan, M.; Wells, N.C. (June 2017). "The impact of future sea-level rise on the global tides". Continental Shelf Research. 142: 50–68. doi:10.1016/j.csr.2017.02.004. ISSN 0278-4343.
  12. ^ a b c d e f g h i j k l m n o p q Pugh, David; Woodworth, Philip (2014). Sea-Level Science. Cambridge: Cambridge University Press. ISBN 978-1-139-23577-8.
  13. ^ a b c d Wang, B. (2003), "Kelvin Waves", Encyclopedia of Atmospheric Sciences, Elsevier, pp. 1062–1068, ISBN 978-0-12-227090-1, retrieved 2021-05-15
  14. ^ a b Charette, Matthew; Smith, Walter (2010-06-01). "The Volume of Earth's Ocean". Oceanography. 23 (2): 112–114. doi:10.5670/oceanog.2010.51. ISSN 1042-8275.
  15. ^ Toffoli, Alessandro; Bitner-Gregersen, Elzbieta M. (2017-03-06), "Types of Ocean Surface Waves, Wave Classification", Encyclopedia of Maritime and Offshore Engineering, Chichester, UK: John Wiley & Sons, Ltd, pp. 1–8, ISBN 978-1-118-47635-2, retrieved 2021-05-15
  16. ^ Hersey, J. B. (1961-11-03). "Physical Oceanography. Albert Defant. Pergamon, New York, 1961. vol. 1, xvi + 729 pp.; vol. 2, viii + 598 pp. Illus. + maps. $35". Science. 134 (3488): 1412–1412. doi:10.1126/science.134.3488.1412. ISSN 0036-8075.
  17. ^ Phillips, Norman A. (1963). "Geostrophic motion". Reviews of Geophysics. 1 (2): 123. doi:10.1029/rg001i002p00123. ISSN 8755-1209.
  18. ^ E., Gill, Aan. Atmosphere--Ocean Dynamics. ISBN 978-1-4832-8158-2. OCLC 952336940.{{cite book}}: CS1 maint: multiple names: authors list (link)
  19. ^ a b c Pugh, D. T. (1981-11-01). "Tidal amphidrome movement and energy dissipation in the Irish Sea". Geophysical Journal International. 67 (2): 515–527. doi:10.1111/j.1365-246x.1981.tb02763.x. ISSN 0956-540X.
  20. ^ Murty, T. S.; Henry, R. F. (1983). "Tides in the Bay of Bengal". Journal of Geophysical Research. 88 (C10): 6069. doi:10.1029/jc088ic10p06069. ISSN 0148-0227.
  21. ^ Sindhu, B.; Unnikrishnan, A. S. (December 2013). "Characteristics of Tides in the Bay of Bengal". Marine Geodesy. 36 (4): 377–407. doi:10.1080/01490419.2013.781088. ISSN 0149-0419.
  22. ^ Cazenave, Anny; Cozannet, Gonéri Le (February 2014). "Sea level rise and its coastal impacts". Earth's Future. 2 (2): 15–34. doi:10.1002/2013ef000188. ISSN 2328-4277.
  23. ^ Church, John A.; White, Neil J. (2011-03-30). "Sea-Level Rise from the Late 19th to the Early 21st Century". Surveys in Geophysics. 32 (4–5): 585–602. doi:10.1007/s10712-011-9119-1. ISSN 0169-3298.
  24. ^ Yin, Jianjun; Griffies, Stephen M.; Stouffer, Ronald J. (2010-09-01). "Spatial Variability of Sea Level Rise in Twenty-First Century Projections". Journal of Climate. 23 (17): 4585–4607. doi:10.1175/2010jcli3533.1. ISSN 1520-0442.
  25. ^ Arns, Arne; Dangendorf, Sönke; Jensen, Jürgen; Talke, Stefan; Bender, Jens; Pattiaratchi, Charitha (2017-01-06). "Sea-level rise induced amplification of coastal protection design heights". Scientific Reports. 7 (1). doi:10.1038/srep40171. ISSN 2045-2322.
Retrieved from "https://en.wikipedia.org/w/index.php?title=Amphidromic_point&oldid=1024971375"