Theory of tides

The theory of tides is the application of continuum mechanics to interpret and predict the tidal deformations of planetary and satellite bodies and their atmospheres and oceans, under the gravitational loading of another astronomical body or bodies. It commonly refers to the fluid dynamic motions for the Earth's oceans.

Origin of theory [edit]

In 1616, Galileo Galilei wrote Discourse on the Tides (in Italian: Discorso del flusso e reflusso del mare),^[1] a paper in which he tried to explain the occurrence of the tides as the result of the Earth's rotation around the Sun. However, Galileo's theory was, in the later Newtonian terms, an error.^[1] In subsequent centuries, further analysis led to the current tidal physics.

Tidal physics [edit]

Tidal forcing [edit]

A. Lunar gravitational potential: this depicts the Moon directly over 30° N (or 30° S) viewed from above the Northern Hemisphere.

B. This view shows same potential from 180° from view A. Viewed from above the Northern Hemisphere. Red up, blue down.

The forces discussed here apply to body (Earth tides), oceanic and atmospheric tides. Atmospheric tides on Earth, however, tend to be dominated by forcing due to solar heating. Oceanic tides act according to the dynamic theory of tides.

On the planet (or satellite) experiencing tidal motion consider a point at latitude $\varphi$ and longitude $\lambda$ at distance $a$ from the center of mass, then this point can be written in cartesian coordinates as $\mathbf{p} = a\mathbf{x}$ where

$\mathbf{x} = (\cos \lambda \cos \varphi, \sin \lambda \cos \varphi, \sin \varphi).$

Let $\delta$ be the declination and $\alpha$ be the right ascension of the deforming body, the Moon for example, then the vector direction is

$\mathbf{x}_m = (\cos \alpha \cos \delta, \sin \alpha \cos \delta, \sin \delta),$

and $r_m$ be the orbital distance between the center of masses and $M_m$ the mass of the body. Then the force on the point is

$\mathbf{F}_{a}= \frac{G M_m (r_m\mathbf{x}_{m}-a\mathbf{x})}{R^3}.$

where $R = \|r_m\mathbf{x}_{m}-a\mathbf{x}\|$

For a circular orbit the angular momentum $\omega$ centripetal acceleration balances gravity at the planetary center of mass

$Mr_{cm}\omega^2= \frac{G M M_m }{r_m^2}.$

where $r_{cm}$ is the distance between the center of mass for the orbit and planet and $M$ is the planetary mass. Consider the point in the reference fixed without rotation, but translating at a fixed translation with respect to the center of mass of the planet. The body's centripetal force acts on the point so that the total force is

$\mathbf{F}_p= \frac{G M_m (r_m\mathbf{x}_{m}-a\mathbf{x})}{R^3} -r_{cm}\omega^2\mathbf{x}_m.$

Substituting for center of mass acceleration, and reordering

$\mathbf{F}_p = G M_m r_m \left( \frac {1}{R^3} - \frac {1}{r_m^3} \right) \mathbf{x}_m -\frac{ ( G M_m a\mathbf{x})}{R^3}.$

In ocean tidal forcing, the radial force is not significant, the next step is to rewrite the $\mathbf{x}_m$ coefficient. Let $\varepsilon= \frac {a} {r_m}$ then

$R = r_m \sqrt{ 1+ \varepsilon ^2-2 \varepsilon ( \mathbf{x}_m,\mathbf{x} ) }$

where $( \mathbf{x}_m,\mathbf{x} )= \cos z$ is the inner product determining the angle z of the deforming body or Moon from the zenith. This means that

$\left( \frac {1}{R^3} - \frac {1}{r_m^3} \right) \approx \frac{3\varepsilon \cos z }{r_m^3},$

if ε is small. If particle is on the surface of the planet then the local gravity is $g=\frac{ G M}{a^2}$ and set $\mu= \frac{M_m} {M}$ .

$\mathbf{F}_p = 3 g \mu \varepsilon^3 \cos z \mathbf{x}_m - \frac{ ( g \mu a^3\mathbf{x})}{R^3} + O(\varepsilon^4),$

which is a small fraction of $g$ . Note also that force is attractive toward the Moon when the $z<\pi/2$ and repulsive when $z > \pi/2$ .

This can also be used to derive a tidal potential.

Laplace's tidal equations [edit]

in 1776, Pierre-Simon Laplace formulated a single set of linear partial differential equations, for tidal flow described as a barotropic two-dimensional sheet flow. Coriolis effects are introduced as well as lateral forcing by gravity. Laplace obtained these equations by simplifying the fluid dynamic equations. But they can also be derived from energy integrals via Lagrange's equation.

For a fluid sheet of average thickness D, the vertical tidal elevation ς, as well as the horizontal velocity components u and v (in the latitude φ and longitude λ directions, respectively) satisfy Laplace's tidal equations:^[2]^[3]

$\begin{align} \frac{\partial \zeta}{\partial t} &+ \frac{1}{a \cos( \varphi )} \left[ \frac{\partial}{\partial \lambda} (uD) + \frac{\partial}{\partial \varphi} \left(vD \cos( \varphi )\right) \right] = 0, \\[2ex] \frac{\partial u}{\partial t} &- v \left( 2 \Omega \sin( \varphi ) \right) + \frac{1}{a \cos( \varphi )} \frac{\partial}{\partial \lambda} \left( g \zeta + U \right) =0 \qquad \text{and} \\[2ex] \frac{\partial v}{\partial t} &+ u \left( 2 \Omega \sin( \varphi ) \right) + \frac{1}{a} \frac{\partial}{\partial \varphi} \left( g \zeta + U \right) =0, \end{align}$

where Ω is the angular frequency of the planet's rotation, g is the planet's gravitational acceleration at the mean ocean surface, and U is the external gravitational tidal-forcing potential.

William Thomson (Lord Kelvin) rewrote Laplace's momentum terms using the curl to find an equation for vorticity. Under certain conditions this can be further rewritten as a conservation of vorticity.

Tidal analysis and prediction [edit]

Harmonic analysis [edit]

Laplace's improvements in theory were substantial, but they still left prediction in an approximate state. This position changed in the 1860s when the local circumstances of tidal phenomena were more fully brought into account by William Thomson's application of Fourier analysis to the tidal motions. Thomson's work in this field was then further developed and extended by George Darwin: Darwin's work was based on the lunar theory current in his time. His symbols for the tidal harmonic constituents are still used. Darwin's harmonic developments of the tide-generating forces were later brought up to date with modern developments by A T Doodson whose development of the tide generating potential (TGP) in harmonic form was carried out and published in 1921:^[4] Doodson distinguished 388 tidal frequencies.^[5] Doodson's analysis of 1921 was based on the then-latest lunar theory of E W Brown.^[6]

Doodson devised a practical system for specifying the different harmonic components of the tide-generating potential, the Doodson Numbers, a system still in use.^[7]

Since the mid-twentieth century further analysis has generated many more terms than Doodson's 388. About 62 constituents are of sufficient size to be considered for possible use in marine tide prediction, but sometimes many less even than that can predict tides to useful accuracy. The calculations of tide predictions using the harmonic constituents are laborious, and from the 1870s to about the 1960s they were carried out using a mechanical tide-predicting machine, a special-purpose form of analog computer now superseded in this work by digital electronic computers that can be programmed to carry out the same computations.

Tidal constituents [edit]

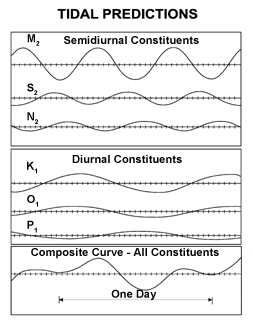
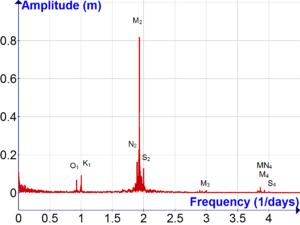
Tidal constituents combine to give an endlessly-varying aggregate because of their different and incommensurable frequencies: the effect is visualized in an animation of the American Mathematical Society illustrating the way in which the components used to be mechanically combined in the tide-predicting machine. Amplitudes of tidal constituents are given below for the following example locations:

ME Eastport,

MS Biloxi,

PR San Juan,

AK Kodiak,

CA San Francisco, and

HI Hilo.

Higher harmonics [edit]	Darwin	Period	Phase	Doodson coefs				Doodson	Amplitude at example location (cm)						NOAA
Species	Symbol	(hr)	rate(°/hr)	n₁ (L)	n₂ (m)	n₃ (y)	n₄ (mp)	number	ME	MS	PR	AK	CA	HI	order
Shallow water overtides of principal lunar	M₄	6.210300601	57.9682084	4				455.555	6.0	0.6		0.9	2.3		5
Shallow water overtides of principal lunar	M₆	4.140200401	86.9523127	6				655.555	5.1	0.1		1.0			7
Shallow water terdiurnal	MK₃	8.177140247	44.0251729	3	1			365.555				0.5	1.9		8
Shallow water overtides of principal solar	S₄	6	60	4	4	-4		491.555		0.1					9
Shallow water quarter diurnal	MN₄	6.269173724	57.4238337	4	-1		1	445.655	2.3			0.3	0.9		10
Shallow water overtides of principal solar	S₆	4	90	6	6	-6		*		0.1					12
Lunar terdiurnal	M₃	8.280400802	43.4761563	3				355.555					0.5		32
Shallow water terdiurnal	2"MK₃	8.38630265	42.9271398	3	-1			345.555	0.5			0.5	1.4		34
Shallow water eighth diurnal	M₈	3.105150301	115.9364166	8				855.555	0.5	0.1					36
Shallow water quarter diurnal	MS₄	6.103339275	58.9841042	4	2	-2		473.555	1.8			0.6	1.0		37
Semi-diurnal [edit]	Darwin	Period	Phase	Doodson coefs				Doodson	Amplitude at example location (cm)						NOAA
Species	Symbol	(hr)	(°/hr)	n₁ (L)	n₂ (m)	n₃ (y)	n₄ (mp)	number	ME	MS	PR	AK	CA	HI	order
Principal lunar semidiurnal	M₂	12.4206012	28.9841042	2				255.555	268.7	3.9	15.9	97.3	58.0	23.0	1
Principal solar semidiurnal	S₂	12	30	2	2	-2		273.555	42.0	3.3	2.1	32.5	13.7	9.2	2
Larger lunar elliptic semidiurnal	N₂	12.65834751	28.4397295	2	-1		1	245.655	54.3	1.1	3.7	20.1	12.3	4.4	3
Larger lunar evectional	ν₂	12.62600509	28.5125831	2	-1	2	-1	247.455	12.6	0.2	0.8	3.9	2.6	0.9	11
Variational	MU₂	12.8717576	27.9682084	2	-2	2		237.555	2.0	0.1	0.5	2.2	0.7	0.8	13
Lunar elliptical semidiurnal second-order	2"N₂	12.90537297	27.8953548	2	-2		2	235.755	6.5	0.1	0.5	2.4	1.4	0.6	14
Smaller lunar evectional	λ₂	12.22177348	29.4556253	2	1	-2	1	263.655	5.3		0.1	0.7	0.6	0.2	16
Larger solar elliptic	T₂	12.01644934	29.9589333	2	2	-3		272.555	3.7	0.2	0.1	1.9	0.9	0.6	27
Smaller solar elliptic	R₂	11.98359564	30.0410667	2	2	-1		274.555	0.9			0.2	0.1	0.1	28
Shallow water semidiurnal	2SM₂	11.60695157	31.0158958	2	4	-4		291.555	0.5						31
Smaller lunar elliptic semidiurnal	L₂	12.19162085	29.5284789	2	1		-1	265.455	13.5	0.1	0.5	2.4	1.6	0.5	33
Lunisolar semidiurnal	K₂	11.96723606	30.0821373	2	2			275.555	11.6	0.9	0.6	9.0	4.0	2.8	35
Diurnal [edit]	Darwin	Period	Phase	Doodson coefs				Doodson	Amplitude at example location (cm)						NOAA
Species	Symbol	(hr)	(°/hr)	n₁ (L)	n₂ (m)	n₃ (y)	n₄ (mp)	number	ME	MS	PR	AK	CA	HI	order
Lunar diurnal	K₁	23.93447213	15.0410686	1	1			165.555	15.6	16.2	9.0	39.8	36.8	16.7	'4
Lunar diurnal	O₁	25.81933871	13.9430356	1	-1			145.555	11.9	16.9	7.7	25.9	23.0	9.2	6
Lunar diurnal	OO₁	22.30608083	16.1391017	1	3			185.555	0.5	0.7	0.4	1.2	1.1	0.7	15
Solar diurnal	S₁	24	15	1	1	-1		164.555	1.0		0.5	1.2	0.7	0.3	17
Smaller lunar elliptic diurnal	M₁	24.84120241	14.4920521	1				155.555	0.6	1.2	0.5	1.4	1.1	0.5	18
Smaller lunar elliptic diurnal	J₁	23.09848146	15.5854433	1	2		-1	175.455	0.9	1.3	0.6	2.3	1.9	1.1	19
Larger lunar evectional diurnal	ρ	26.72305326	13.4715145	1	-2	2	-1	137.455	0.3	0.6	0.3	0.9	0.9	0.3	25
Larger lunar elliptic diurnal	Q₁	26.868350	13.3986609	1	-2		1	135.655	2.0	3.3	1.4	4.7	4.0	1.6	26
Larger elliptic diurnal	2Q₁	28.00621204	12.8542862	1	-3		2	125.755	0.3	0.4	0.2	0.7	0.4	0.2	29
Solar diurnal	P₁	24.06588766	14.9589314	1	1	-2		163.555	5.2	5.4	2.9	12.6	11.6	5.1	30
Long period [edit]	Darwin	Period	Phase	Doodson coefs				Doodson	Amplitude at example location (cm)						NOAA
Species	Symbol	(hr)	(°/hr)	n₁ (L)	n₂ (m)	n₃ (y)	n₄ (mp)	number	ME	MS	PR	AK	CA	HI	order
Lunar monthly	M_m	661.3111655	0.5443747	0	1		-1	65.455			0.7	1.9			20
Solar semiannual	S_sa	4383.076325	0.0821373	0		2		57.555	1.6		2.1	1.5	3.9		21
Solar annual	S_a	8766.15265	0.0410686	0		1		56.555			5.5	7.8	3.8	4.3	22
Lunisolar synodic fortnightly	M_sf	354.3670666	1.0158958	0	2	-2		73.555				1.5			23
Lunisolar fortnightly	M_f	327.8599387	1.0980331	0	2			75.555			1.4	2.0		0.7	24

Dynamic theory of tides [edit]

While Newton explained the tides by describing the tide generating forces, and Bernoulli gave a description of the static reaction of the waters on earth to the tidal potential, the dynamic theory of tides, first introduced by Laplace, describes the ocean's real reaction to the forces. This theory of ocean tides took into account friction, resonance and natural periods of ocean basins. It predicted amphidromic circulation. The presence of large amphidromic systems in the world's ocean basins was long ago theorized, to explain the oceanic tides that are actually observed. The twin bulge theory, based on the actual gravitational gradient from the sun and moon, couldn't explain the various ocean tides.^[8]^[9]^[10]^[11]^[12]^[13]^[14]^[15]^[16] Since measurements have confirmed the theory, many things have possible explanations now, like how the tides interact with deep sea ridges and chains of seamounts give rise to deep eddies that transport nutrients from the deep to the surface.^[17] The equilibrium tide theory calculates the height of the tide wave of less than half a meter, while the dynamic theory explains why tides are up to 15 meters.^[18]

The theory was developed by Pierre-Simon Laplace in 1775.^[19] Satellite data has confirmed the Dynamic theory as accurate, and the tides worldwide are now measured to within a few centimeters.^[20]^[21] Measurements from the CHAMP satellite closely matches the models based on the TOPEX data.^[22]^[23] Accurate models of tides worldwide are essential for research since the variations due to tides must be removed from measurements when calculating gravity and changes in sea levels.^[24]

References and notes [edit]

^ ^a ^b Rice University - Galileo's Theory of the Tides - by Rossella Gigli, retrieved 10 March 2010
^ http://kiwi.atmos.colostate.edu/group/dave/pdf/LTE.frame.pdf
^ http://siam.org/pdf/news/621.pdf
^ A T Doodson (1921), "The Harmonic Development of the Tide-Generating Potential", Proceedings of the Royal Society of London. Series A, Vol. 100, No. 704 (Dec. 1, 1921), pp. 305-329.
^ S Casotto, F Biscani, "A fully analytical approach to the harmonic development of the tide-generating potential accounting for precession, nutation, and perturbations due to figure and planetary terms", AAS Division on Dynamical Astronomy, April 2004, vol.36(2), 67.
^ D E Cartwright, "Tides: a scientific history", Cambridge University Press 2001, at pages 163-4.
^ See e.g. T D Moyer (2003), "Formulation for observed and computed values of Deep Space Network data types for navigation", vol.3 in Deep-space communications and navigation series, Wiley (2003), e.g. at pp.126-8.
^ Tidal theory website South African Navy Hydrographic Office
^ "Dynamic theory for tides". Oberlin.edu. Retrieved 2012-06-02.
^ http://ffden-2.phys.uaf.edu/645fall2003_web.dir/ellie_boyce/dynamic.htm
^ "Tides and their seminal impact on the geology, geography, history, and socio-economics of the Bay of Fundy, eastern Canada | Desplanque | Atlantic Geology". Journals.hil.unb.ca. Retrieved 2012-06-02.
^ "Dynamic Tides – In contrast to "static" theory, the dynamic theory of tides recognizes that water covers only three-quarters o". Web.vims.edu. Retrieved 2012-06-02.
^ "The Dynamic Theory of Tides". Coa.edu. Retrieved 2012-06-02.
^ https://beacon.salemstate.edu/~lhanson/gls214/gls214_tides
^ "Tides - building, river, sea, depth, oceans, effects, important, largest, system, wave, effect, marine, Pacific". Waterencyclopedia.com. 2010-06-27. Retrieved 2012-06-02.
^ "TIDES". Ocean.tamu.edu. Retrieved 2012-06-02.
^ Floor Anthoni. "Tides". Seafriends.org.nz. Retrieved 2012-06-02.
^ http://www.linz.govt.nz/hydro/tidal-info/tidal-intro/cause-nature
^ "Shelf and Coastal Oceanography". Es.flinders.edu.au. Retrieved 2012-06-02.
^ "Scientific Visualization Studio TOPEX/Poseidon images". Svs.gsfc.nasa.gov. Retrieved 2012-06-02.
^ "TOPEX/Poseidon Western Hemisphere: Tide Height Model : NASA/Goddard Space Flight Center Scientific Visualization Studio : Free Download & Streaming : Internet Archive". Archive.org. Retrieved 2012-06-02.
^ http://www.geomag.us/info/Ocean/m2_CHAMP+longwave_SSH.swf
^ "OSU Tidal Data Inversion". Volkov.oce.orst.edu. Retrieved 2012-06-02.
^ http://www.dgfi.badw.de/index.php?id=143

External links [edit]

[Galileo.27s_Theory_of_the_Tides-1] Rice University - Galileo's Theory of the Tides - by Rossella Gigli, retrieved 10 March 2010

[2] ttp://kiwi.atmos.colostate.edu/group/dave/pdf/LTE.frame.pdf

[3] ttp://siam.org/pdf/news/621.pdf

[4] A T Doodson (1921), "The Harmonic Development of the Tide-Generating Potential", Proceedings of the Royal Society of London. Series A, Vol. 100, No. 704 (Dec. 1, 1921), pp. 305-329.

[5] S Casotto, F Biscani, "A fully analytical approach to the harmonic development of the tide-generating potential accounting for precession, nutation, and perturbations due to figure and planetary terms", AAS Division on Dynamical Astronomy, April 2004, vol.36(2), 67.

[dec2001-6] D E Cartwright, "Tides: a scientific history", Cambridge University Press 2001, at pages 163-4.

[7] See e.g. T D Moyer (2003), "Formulation for observed and computed values of Deep Space Network data types for navigation", vol.3 in Deep-space communications and navigation series, Wiley (2003), e.g. at pp.126-8.

[8] Tidal theory website South African Navy Hydrographic Office

[9] "Dynamic theory for tides". Oberlin.edu. Retrieved 2012-06-02.

[10] ttp://ffden-2.phys.uaf.edu/645fall2003_web.dir/ellie_boyce/dynamic.htm

[11] "Tides and their seminal impact on the geology, geography, history, and socio-economics of the Bay of Fundy, eastern Canada | Desplanque | Atlantic Geology". Journals.hil.unb.ca. Retrieved 2012-06-02.

[12] "Dynamic Tides – In contrast to "static" theory, the dynamic theory of tides recognizes that water covers only three-quarters o". Web.vims.edu. Retrieved 2012-06-02.

[13] "The Dynamic Theory of Tides". Coa.edu. Retrieved 2012-06-02.

[14] ttps://beacon.salemstate.edu/~lhanson/gls214/gls214_tides

[15] "Tides - building, river, sea, depth, oceans, effects, important, largest, system, wave, effect, marine, Pacific". Waterencyclopedia.com. 2010-06-27. Retrieved 2012-06-02.

[16] "TIDES". Ocean.tamu.edu. Retrieved 2012-06-02.

[17] Floor Anthoni. "Tides". Seafriends.org.nz. Retrieved 2012-06-02.

[18] ttp://www.linz.govt.nz/hydro/tidal-info/tidal-intro/cause-nature

[19] "Shelf and Coastal Oceanography". Es.flinders.edu.au. Retrieved 2012-06-02.

[20] "Scientific Visualization Studio TOPEX/Poseidon images". Svs.gsfc.nasa.gov. Retrieved 2012-06-02.

[21] "TOPEX/Poseidon Western Hemisphere: Tide Height Model : NASA/Goddard Space Flight Center Scientific Visualization Studio : Free Download & Streaming : Internet Archive". Archive.org. Retrieved 2012-06-02.

[22] ttp://www.geomag.us/info/Ocean/m2_CHAMP+longwave_SSH.swf

[23] "OSU Tidal Data Inversion". Volkov.oce.orst.edu. Retrieved 2012-06-02.

[24] ttp://www.dgfi.badw.de/index.php?id=143

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

Theory of tides

Contents

Origin of theory [edit]

Tidal physics [edit]

Tidal forcing [edit]

Laplace's tidal equations [edit]

Tidal analysis and prediction [edit]

Harmonic analysis [edit]

Tidal constituents [edit]

Higher harmonics [edit]

Semi-diurnal [edit]

Diurnal [edit]

Long period [edit]

Dynamic theory of tides [edit]

See also [edit]

References and notes [edit]

External links [edit]

Navigation menu

Personal tools

Namespaces

Variants

Views

Actions

Search

Navigation

Interaction

Toolbox

Print/export

Languages