Binary search tree

Binary search tree
Binary search tree
Type	tree
Invented	1960
Invented by	P.F. Windley, A.D. Booth, A.J.T. Colin, and T.N. Hibbard
Operation
Time complexity in big O notation
Operation	Average
Search	O(log n)
Insert	O(log n)
Delete	O(log n)
Space complexity
Space	O(n)

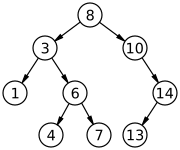
In computer science, a binary search tree (BST), also called an ordered or sorted binary tree, is a rooted binary tree data structure whose internal nodes each store a key greater than all the keys in the node's left subtree and less than those in its right subtree. The time complexity of operations on the binary search tree is directly proportional to the height of the tree.

Binary search trees allow binary search for fast lookup, addition, and removal of data items, and can be used to implement dynamic sets and lookup tables. Since the nodes in a BST are laid out in such a way that each comparison skips about half of the remaining tree, the lookup performance is proportional to that of binary logarithm.

The performance of a binary search tree is dependent on the order of insertion of the nodes into the tree; several variations of the binary search tree can be built with guaranteed worst-case performance. The basic operations include: search, traversal, insert and delete. BSTs with guaranteed worst-case complexities perform better than an unsorted array, which would require linear search time.

The complexity analysis of BST shows that, on average, the insert, delete and search takes $O(\log n)$ for $n$ nodes. In the worst case, they degrade to that of a singly linked list: $O(n)$ .

History

The binary search tree algorithm was discovered independently by several researchers, including P.F. Windley, Andrew Donald Booth, Andrew Colin, Thomas N. Hibbard, and attributed to Conway Berners-Lee and David Wheeler, in 1960 for storing labeled data in magnetic tapes.^[1]^[2]^[3]

Definition

A binary search tree, also known as ordered binary search tree, is a variation of rooted binary tree in which the nodes are arranged in an order.^[4]^: 298 The nodes of the tree store a key (and optionally, an associated value), and each has two distinguished sub-trees, commonly denoted left and right. The tree additionally satisfies the binary search property: the key in each node is greater than any key stored in the left sub-tree, and less than or equal to any key stored in the right sub-tree.^[5]^: 287

BST requires an order relation by which every node of the tree is comparable with every other node in the sense of total order. Binary search trees are also efficacious in sorting algorithms and search algorithms. However, the search complexity of a BST depends upon the order in which the nodes are inserted and deleted; since in worst case, successive operations in the binary search tree may lead to degeneracy and form a singly linked list (or "unbalanced tree") like structure, thus has the same worst-case complexity as a linked list.^[6]^[4]^: 299-302 Binary search trees are also a fundamental data structure used in construction of abstract data structures such as sets, multisets, and associative arrays.

Operations

Binary search trees support three main operations: lookup (checking whether a key is present), insertion, and deletion of an element. The latter two possibly change the structural arrangement of the nodes in the tree, whereas the first one is a navigating and read-only operation. Other read-only operations are traversal, verification, etc.

Searching

Searching in a binary search tree for a specific key can be programmed recursively or iteratively.

Searching begins by examining the root node. If the tree is ${\text{nil}}$ , the key being searched for does not exist in the tree. Otherwise, if the key equals that of the root, the search is successful and the node is returned. If the key is less than that of the root, the search proceeds by examining the left subtree. Similarly, if the key is greater than that of the root, the search proceeds by examining the right subtree. This process is repeated until the key is found or the remaining subtree is ${\text{nil}}$ . If the searched key is not found after a ${\text{nil}}$ subtree is reached, then the key is not present in the tree.

Recursive search

The following pseudocode implements the BST search procedure through recursion.^[5]^: 290

 Tree-Search(x, key)
   if x = NIL or key = x.key then
     return x
   if key < x.key then
     return Tree-Search(x.left, key)
   else
     return Tree-Search(x.right, key)
   end if

The recursive procedure continues until a ${\text{nil}}$ or the ${\text{key}}$ being searched for are encountered.

Iterative search

The recursive version of the search can be "unrolled" into a while loop. On most machines, the iterative version is found to be more efficient.^[5]^: 291

 Iterative-Tree-Search(x, key)
   while x ≠ NIL and key ≠ x.key then
     if key < x.key then
       x := x.left
     else
       x := x.right
     end if
   repeat
   return x

Since the search may proceed till some leaf node, the running time complexity of BST search is $O(h)$ where $h$ is the height of the tree. However, the worst case for BST search is $O(n)$ where $n$ is the total number of nodes in the BST, because an unbalanced BST may degenerate to a linked list. However, if the BST is height-balanced the height is $O(\log n)$ .^[5]^: 290

Successor and predecessor

For certain operations, given a node ${\text{x}}$ , finding the successor or predecessor of ${\text{x}}$ is crucial. Assuming all the keys of the BST are distinct, the successor of a node ${\text{x}}$ in BST is the node with the smallest key greater than ${\text{x}}$ 's key. On the other hand, the predecessor of a node ${\text{x}}$ in BST is the node with the largest key smaller than ${\text{x}}$ 's key. Following is pseudocode for finding the successor and predecessor of a node ${\text{x}}$ in BST.^[5]^{: 292–293}

 Tree-Successor(x)
   if x.right ≠ NIL then
     return Tree-Minimum(x.right)
   end if
   y := x.parent
   while y ≠ NIL and x = y.right then
     x := y
     y := y.parent
   repeat
   return y

 Tree-Predecessor(x)
   if x.left ≠ NIL then
     return Tree-Maximum(x.left)
   end if
   y := x.parent
   while y ≠ NIL and x = y.left then
     x := y
     y := y.parent
   repeat
   return y

Operations such as finding a node in a BST whose key is the maximum or minimum are critical in certain operations, such as determining the successor and predecessor of nodes. Following is the pseudocode for the operations.^[5]^{: 291–292}

 Tree-Maximum(x)
   while x.right ≠ NIL then
     x := x.right
   repeat
   return x

 Tree-Minimum(x)
   while x.left ≠ NIL then
     x := x.left
   repeat
   return x

Insertion

Operations such as insertion and deletion cause the BST representation to change dynamically. The data structure must be modified in such a way that the properties of BST continue to hold. New nodes are inserted as leaf nodes in the BST.^[5]^{: 294–295} Following is an iterative implementation of the insertion operation.^[5]^: 294

1    Tree-Insert(T, z)
2      y := NIL
3      x := T.root
4      while x ≠ NIL do
5        y := x
6        if z.key < x.key then
7          x := x.left
8        else
9          x := x.right
10       end if
11    repeat
12    z.parent := y
13    if y = NIL then
14      T.root := z
15    else if z.key < y.key then
16      y.left := z
17    else
18      y.right := z
19    end if

The procedure maintains a "trailing pointer" ${\text{y}}$ as a parent of ${\text{x}}$ . After initialization on line 2, the while loop along lines 4-11 causes the pointers to be updated. If ${\text{y}}$ is ${\text{nil}}$ , the BST is empty, thus ${\text{z}}$ is inserted as the root node of the binary search tree ${\text{T}}$ , if it isn't ${\text{nil}}$ , insertion proceeds by comparing the keys to that of ${\text{y}}$ on the lines 15-19 and the node is inserted accordingly.^[5]^: 295

Deletion

File:Binary search tree deletion illustration.png

Fig. 2: Binary search tree special cases deletion illustration.

Deletion of a node, say ${\text{z}}$ , from a binary search tree ${\text{T}}$ should abide three cases:^[5]^: 295

If ${\text{z}}$ is a leaf node, the parent node's pointer to ${\text{z}}$ gets replaced with ${\text{nil}}$ and consequently ${\text{z}}$ gets removed from the tree.
If ${\text{z}}$ has a single child node, the child gets elevated as either left or right child of ${\text{z}}$ 's parent depending on the position of ${\text{z}}$ within the BST, as shown in fig. 2 part (a) and part (b), and as a result, ${\text{z}}$ gets removed from the tree.
If ${\text{z}}$ ${\text{z}}$ has both a left and right child, the successor of ${\text{z}}$ ${\text{z}}$ (let it be ${\text{y}}$ ${\text{y}}$ ) takes the position of ${\text{z}}$ ${\text{z}}$ in the tree. This depends on the position of ${\text{y}}$ ${\text{y}}$ within the BST:^[5]^: 296
1. If ${\text{y}}$ is ${\text{z}}$ 's immediate right child, ${\text{y}}$ gets elevated and ${\text{y}}$ 's left child made point to ${\text{z}}$ 's initial left sub-tree, as shown in fig. 2 part (c).
2. If ${\text{y}}$ isn't the immediate right child of ${\text{z}}$ , deletion proceeds by replacing the position of ${\text{y}}$ by its right child, and ${\text{y}}$ takes the position of ${\text{z}}$ in the BST, as shown in fig. 2 part (d).

Following is a pseudocode for the deletion operation in a binary search tree.^[5]^: 296-298

1    Tree-Delete(T, z)
2      if z.left = NIL then
3        Subtree-Shift(T, z, z.right)
4      else if z.right = NIL then
5        Subtree-Shift(T, z, z.left)
6      else
7        y := Tree-Successor(z)
8        if y.parent ≠ z then
9          Subtree-Shift(T, y, y.right)
10         y.right := z.right
11         y.right.parent := y
12       end if
13       Subtree-Shift(T, z, y)
14       y.left := z.left
15       y.left.parent := y
16     end if

1    Subtree-Shift(T, u, v)
2      if u.parent = NIL then
3        T.root := v
4      else if u = u.parent.left then
5        u.parent.left := v
5      else
6        u.parent.right := v
7      end if
8      if v ≠ NIL then
9        v.parent := u.parent
10     end if

The ${\text{Tree-Delete}}$ procedure deals with the 3 special cases mentioned above. Lines 2-3 deal with case 1; lines 4-5 deal with case 2 and lines 6-16 for case 3. The helper function ${\text{Subtree-Shift}}$ is used within the deletion algorithm for the purpose of replacing the node ${\text{u}}$ with ${\text{v}}$ in the binary search tree ${\text{T}}$ .^[5]^: 298 This procedure handles the deletion (and substitution) of ${\text{u}}$ from the BST.

Traversal

A BST can be traversed through three basic algorithms: inorder, preorder, and postorder tree walks.^[5]^: 287

Inorder tree walk: Nodes from the left subtree get visited first, followed by the root node and right subtree.
Preorder tree walk: The root node gets visited first, followed by left and right subtrees.
Postorder tree walk: Nodes from the left subtree get visited first, followed by the right subtree, and finally the root.

Following is a recursive implementation of the tree walks.^[5]^{: 287–289}

 Inorder-Tree-Walk(x)
   if x ≠ NIL then
     Inorder-Tree-Walk(x.left)
     visit node
     Inorder-Tree-Walk(x.right)
   end if

 Preorder-Tree-Walk(x)
   if x ≠ NIL then
     visit node
     Preorder-Tree-Walk(x.left)
     Preorder-Tree-Walk(x.right)
   end if

 Postorder-Tree-Walk(x)
   if x ≠ NIL then
     Postorder-Tree-Walk(x.left)
     Postorder-Tree-Walk(x.right)
     visit node
   end if

Examples of applications

Sort

A binary search tree can be used in sorting algorithm implementation. The process involves inserting all the elements which are to be sorted and performing inorder traversal. This method is similar to that of quicksort where each node corresponds to a partitioning item that subdivides its descendants into smaller keys and larger keys.^[7]

Priority queue operations

Binary search trees are used in implementing priority queues, using the element or node's key as priorities. Adding new elements to the queue follows the regular BST ${\text{Tree-Insert}}$ operation; but the removal operation depends on the type of priority queue:^[8]

If it's an ascending order priority queue, removal of an element with the lowest priority is done through leftward traversal of the BST i.e. ${\text{Tree-Minimum }}$ .
On the other hand, if it's a descending order priority queue, removal of an element with the highest priority is done through rightward traversal of the BST i.e. ${\text{Tree-Maximum }}$ .

Types

There are many types of binary search trees.

Self-balancing binary search trees modify the basic insertion and deletion operations of binary search trees, often using additional information on each node, in order to maintain logarithmic depth. These include two early structures of this type, AVL trees, which maintain an invariant that subtree heights differ by at most one, and red–black trees, which instead color nodes red or black and maintain an invariant on the number of colored nodes on each root-to-leaf path. These two types of trees are unified in the WAVL tree.

The T-tree is a height-balanced binary search tree optimized to reduce storage space overhead which are used for in-memory databases.^[9]

Weight-balanced trees achieve (a worst-case logarithmic time bound for searching and) constant time bounds (in an amortized sense: summing over whole sequences of operations rather than analysing the time for each operation independently) for the update^[10] operations, but can be more flexible as part of recursive structures used in range searching. When keys are inserted in a random order to a non-self-balancing binary tree, or drawn independently from a random distribution, without deletions, the resulting random binary search tree has both logarithmic expected depth, and logarithmic worst-case depth with high probability.

The treap (tree heap) is a self-balancing version of binary search trees that obtains the same behavior for worst-case operations, by assigning random priorities to each key and using the priorities to structure the tree as a Cartesian tree, with higher priorities at each node than at its children.

Certain types of self-balancing binary search trees have been designed to take advantage of non-uniform access patterns by handling frequently requested keys more quickly. The performance of these online binary search trees can be analyzed by their competitive ratio, the maximum possible ratio of its running time on a sequence of access requests compared to the time of the best possible self-balancing binary search tree for the same access request. Splay trees have been conjectured to have a constant competitive ratio, but this has not been proven. The geometry of binary search trees gives a way of reformulating these problems geometrically, in terms of augmenting point sets to avoid axis-parallel rectangles with only two diagonal vertices present in the augmented set. Another online binary search tree, the tango tree, is inspired by this geometric formulation, and has been proven to achieve an $O(\log \log n)$ competitive ratio, while only using $O(\log \log n)$ additional bits of memory per node.^[11]

A binary search tree may be "degenerate", by having only left children at every node, or by having only right children at every node. When the resulting degenerate binary search tree contains $n$ nodes it has height of $n-1$ . The performance or time complexity of a lookup operation is essentially identical with that of a linear search i.e. $O(n)$ , which is alike that of data structures like arrays or linked lists.^[12]

Performance comparisons

In regards to performance characteristics of binary search trees, a study shows that treaps perform better on average case, while red–black tree was found to have the smallest number of performance variations.^[13]

Optimal binary search trees

Optimal binary search tree is a theoretical computer science problem which deals with constructing an "optimal" binary search trees that enables smallest possible search time for a given sequence of accesses.^[14]^{: 449–450} The computational cost required to maintain an "optimal" search tree can be justified if search is more dominant activity in the tree than insertion or deletion.^[15]^[14]^: 449

Threaded binary trees

A threaded binary search tree is an accessorial version of a binary tree whose ${\text{nil}}$ pointers—either left or right fields of a node—points to the inorder successor or inorder predecessor of the given nodes such that efficient utilization of the placeholders fields are performed.^[4]^: 311-312 Threading is classified into two categories:^[4]^: 312

One-way threading: The left or right pointer field of the nodes, holds a reference to the inorder predecessor or inorder successor, but not both.
Two-way threading: The left and right pointer fields hold the references to the inorder predecessor and inorder successor respectively.

References

^ Culberson, J.; Munro, J. I. (1 January 1989). "Explaining the Behaviour of Binary Search Trees Under Prolonged Updates: A Model and Simulations". The Computer Journal. 32 (1): 68-69. doi:10.1093/comjnl/32.1.68.
^ Culberson, J.; Munro, J. I. (28 July 1986). "Analysis of the standard deletion algorithms in exact fit domain binary search trees". Algorithmica. Springer Publishing, University of Waterloo: 297. doi:10.1007/BF01840390.
^ P. F. Windley (1 January 1960). "Trees, Forests and Rearranging". The Computer Journal. 3 (2): 84. doi:10.1093/comjnl/3.2.84.
^ ^a ^b ^c ^d Thareja, Reema (13 October 2018). "Hashing and Collision". Data Structures Using C (2 ed.). Oxford University Press. ISBN 9780198099307.
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m ⁿ ^o Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). Introduction to Algorithms (2nd ed.). MIT Press. ISBN 0-262-03293-7.
^ R. A. Frost; M. M. Peterson (1 February 1982). "A Short Note on Binary Search Trees". The Computer Journal. 25 (1). Oxford University Press: 158. doi:10.1093/comjnl/25.1.158.
^ Narayanan, Arvind (2019). "COS226: Binary search trees". Princeton University School of Engineering and Applied Science. Archived from the original on 22 March 2021. Retrieved 21 October 2021 – via cs.princeton.edu.
^ Myers, Andrew. "CS 2112 Lecture and Recitation Notes: Priority Queues and Heaps". Cornell University, Department of Computer Science. Archived from the original on 21 October 2021. Retrieved 21 October 2021.
^ Lehman, Tobin J.; Carey, Michael J. (25–28 August 1986). A Study of Index Structures for Main Memory Database Management Systems. Twelfth International Conference on Very Large Databases (VLDB 1986). Kyoto. ISBN 0-934613-18-4.
^ Blum, Norbert; Mehlhorn, Kurt (1978). "On the Average Number of Rebalancing Operations in Weight-Balanced Trees" (PDF). Theoretical Computer Science. 11 (3): 303–320. doi:10.1016/0304-3975(80)90018-3.
^ Demaine, E. D.; Harmon, D.; Iacono, J.; Pătraşcu, M. (2007). "Dynamic Optimality—Almost" (PDF). SIAM Journal on Computing. 37 (1): 240. doi:10.1137/S0097539705447347. S2CID 1480961. Archived (PDF) from the original on 27 February 2021 – via erikdemaine.org.
^ Thornton, Alex (2021). "ICS 46: Binary Search Trees". University of California, Irvine. Archived from the original on 4 July 2021. Retrieved 21 October 2021.
^ Heger, Dominique A. (2004), "A Disquisition on The Performance Behavior of Binary Search Tree Data Structures" (PDF), European Journal for the Informatics Professional, 5 (5): 67–75, archived from the original (PDF) on 2014-03-27, retrieved 2010-10-16 – via Archive.org
^ ^a ^b Korah, A.P.; Kaimal, M.R. (1990). "Dynamic Optimal Binary Search Tree". International Journal of Foundations of Computer Science. 1 (4): 449–463. doi:10.1142/S0129054190000308 – via World Scientific.
^ Gonnet, Gaston. "Optimal Binary Search Trees". Scientific Computation. ETH Zürich. Archived from the original on 12 October 2014. Retrieved 1 December 2013.

External links

Ben Pfaff: An Introduction to Binary Search Trees and Balanced Trees. (PDF; 1675 kB) 2004.
Binary Tree Visualizer (JavaScript animation of various BT-based data structures)

[1] Culberson, J.; Munro, J. I. (1 January 1989). "Explaining the Behaviour of Binary Search Trees Under Prolonged Updates: A Model and Simulations". The Computer Journal. 32 (1): 68-69. doi:10.1093/comjnl/32.1.68.

[2] Culberson, J.; Munro, J. I. (28 July 1986). "Analysis of the standard deletion algorithms in exact fit domain binary search trees". Algorithmica. Springer Publishing, University of Waterloo: 297. doi:10.1007/BF01840390.

[3] P. F. Windley (1 January 1960). "Trees, Forests and Rearranging". The Computer Journal. 3 (2): 84. doi:10.1093/comjnl/3.2.84.

[reema18-4] Thareja, Reema (13 October 2018). "Hashing and Collision". Data Structures Using C (2 ed.). Oxford University Press. ISBN 9780198099307.

[algo_cormen-5] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m ⁿ ^o Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). Introduction to Algorithms (2nd ed.). MIT Press. ISBN 0-262-03293-7.

[6] R. A. Frost; M. M. Peterson (1 February 1982). "A Short Note on Binary Search Trees". The Computer Journal. 25 (1). Oxford University Press: 158. doi:10.1093/comjnl/25.1.158.

[7] Narayanan, Arvind (2019). "COS226: Binary search trees". Princeton University School of Engineering and Applied Science. Archived from the original on 22 March 2021. Retrieved 21 October 2021 – via cs.princeton.edu.

[8] Myers, Andrew. "CS 2112 Lecture and Recitation Notes: Priority Queues and Heaps". Cornell University, Department of Computer Science. Archived from the original on 21 October 2021. Retrieved 21 October 2021.

[9] Lehman, Tobin J.; Carey, Michael J. (25–28 August 1986). A Study of Index Structures for Main Memory Database Management Systems. Twelfth International Conference on Very Large Databases (VLDB 1986). Kyoto. ISBN 0-934613-18-4.

[10] Blum, Norbert; Mehlhorn, Kurt (1978). "On the Average Number of Rebalancing Operations in Weight-Balanced Trees" (PDF). Theoretical Computer Science. 11 (3): 303–320. doi:10.1016/0304-3975(80)90018-3.

[DHIP-11] Demaine, E. D.; Harmon, D.; Iacono, J.; Pătraşcu, M. (2007). "Dynamic Optimality—Almost" (PDF). SIAM Journal on Computing. 37 (1): 240. doi:10.1137/S0097539705447347. S2CID 1480961. Archived (PDF) from the original on 27 February 2021 – via erikdemaine.org.

[12] Thornton, Alex (2021). "ICS 46: Binary Search Trees". University of California, Irvine. Archived from the original on 4 July 2021. Retrieved 21 October 2021.

[13] Heger, Dominique A. (2004), "A Disquisition on The Performance Behavior of Binary Search Tree Data Structures" (PDF), European Journal for the Informatics Professional, 5 (5): 67–75, archived from the original (PDF) on 2014-03-27, retrieved 2010-10-16 – via Archive.org

[optimal_tree_90-14] Korah, A.P.; Kaimal, M.R. (1990). "Dynamic Optimal Binary Search Tree". International Journal of Foundations of Computer Science. 1 (4): 449–463. doi:10.1142/S0129054190000308 – via World Scientific.

[15] Gonnet, Gaston. "Optimal Binary Search Trees". Scientific Computation. ETH Zürich. Archived from the original on 12 October 2014. Retrieved 1 December 2013.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

v t e Tree data structures
Search trees (dynamic sets/associative arrays)	2–3 2–3–4 AA (a,b) AVL B B+ B* B^x (Optimal) Binary search Dancing HTree Interval Order statistic (Left-leaning) Red–black Scapegoat Splay T Treap UB Weight-balanced
Heaps	Binary Binomial Brodal d-ary Fibonacci Leftist Pairing Skew binomial Skew van Emde Boas Weak
Tries	Ctrie C-trie (compressed ADT) Hash Radix Suffix Ternary search X-fast Y-fast
Spatial data partitioning trees	Ball BK BSP Cartesian Hilbert R k-d (implicit k-d) M Metric MVP Octree PH Priority R Quad R R+ R* Segment VP X
Other trees	Cover Exponential Fenwick Finger Fractal tree index Fusion Hash calendar iDistance K-ary Left-child right-sibling Link/cut Log-structured merge Merkle PQ Range SPQR Top

v t e Data structures
Types	Collection Container
Abstract	Associative array Multimap Retrieval Data Structure List Stack Queue Double-ended queue Priority queue Double-ended priority queue Set Multiset Disjoint-set
Arrays	Bit array Circular buffer Dynamic array Hash table Hashed array tree Sparse matrix
Linked	Association list Linked list Skip list Unrolled linked list XOR linked list
Trees	B-tree Binary search tree AA tree AVL tree Red–black tree Self-balancing tree Splay tree Heap Binary heap Binomial heap Fibonacci heap R-tree R* tree R+ tree Hilbert R-tree Trie Hash tree
Graphs	Binary decision diagram Directed acyclic graph Directed acyclic word graph
List of data structures