Empirical evidence for the spherical shape of Earth

The roughly spherical shape of Earth can be empirically evidenced by many different types of observation, ranging from ground level, flight, or orbit. The spherical shape causes a number of effects and phenomena that combined disprove flat Earth beliefs. These include the visibility of distant objects on Earth's surface; lunar eclipses; appearance of the Moon; observation of the sky from altitude; observation of certain fixed stars from different locations; observing the Sun; surface navigation; grid distortion on a spherical surface; weather systems; gravity; and modern technology.

Visibility of distant objects on Earth's surface

Main article: Horizon § Distance to the horizon

Graphs of distances to the true horizon on Earth for a given height h. s is along the surface of Earth, d is the straight line distance, and ~d is the approximate straight line distance assuming h << the radius of Earth, 6371 km. In the SVG image, hover over a graph to highlight it.

On a completely flat Earth without obstructions (mountains, hills, valleys or volcanos), the ground itself would never obscure distant objects. A spherical surface has a horizon which is closer when viewed from a lower altitude. In theory, a person standing on the surface with eyes 1.8 metres (5 ft 11 in) above the ground can see the ground up to about 4.79 kilometres (2.98 mi) away, but a person at the top of the Eiffel Tower at 273 metres (896 ft) can see the ground up to about 58.98 kilometres (36.65 mi) away.

This phenomenon permits a way of confirming that Earth's surface is locally convex: If the degree of curvature is determined to be the same everywhere on Earth's surface, and that surface was determined to be large enough, the constant curvature would show that Earth is spherical. In practice, this method is not reliable because of variations in atmospheric refraction, which is how much the atmosphere bends light traveling through it. Refraction can give the impression that Earth's surface is flat, curved more convexly than it is, or even that it is concave (this is what happened in various trials of the Bedford Level experiment).

The phenomenon of variable atmospheric bending can be seen when distant objects appear to be broken into pieces or even turned upside down. This is often seen at sunset, when the Sun's shape is distorted, but has also been photographed happening to ships, and has caused the city of Chicago to appear normally, upside down, and broken into pieces from across Lake Michigan (from where it is normally below the horizon).

When the atmosphere is relatively well-mixed, the visual effects generally expected of a spherical Earth can be observed. For example, ships travelling on large bodies of water (such as the ocean) disappear over the horizon progressively, such that the highest part of the ship can still be seen even when lower parts cannot, proportional to distance from the observer. Likewise, in the days of sailing ships, a sailor would climb up a mast to see farther. The same is true of the coastline or mountain when viewed from a ship or from across a large lake or flat terrain. In certain places, the curvature is visible via fixed objects. This includes the 23 mile Lake Pontchartrain Causeway visible from a Metairie hotel, and the 85 pylons carrying 15 miles of powerlines over Lake Pontchartrain, visible from I-10 Bonnet Carré Spillway Bridge.

Lunar eclipses

Latter phases of the partial lunar eclipse on 17 July 2019 taken from Gloucestershire, United Kingdom

The shadow of Earth on the Moon during a lunar eclipse is always a dark circle that moves from one side of the Moon to the other (partially grazing it during a partial eclipse). The only shape that casts a round shadow no matter which direction it is pointed is a sphere, and the ancient Greeks deduced that this must mean Earth is spherical.

The effect could be produced by a disk that always faces the Moon head-on during the eclipse, but this is inconsistent with the fact that the Moon is only rarely directly overhead during an eclipse. For each eclipse, the local surface of Earth is pointed in a different direction. The shadow of a disk held at an angle is an oval, not a circle as is seen during the eclipse. The idea of Earth being a disk is also inconsistent with the fact that a given lunar eclipse is only visible from half of Earth at a time.

Appearance of the Moon

The Moon tidally locked to Earth (left) and how it would be without tidal lock (right)

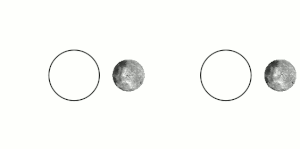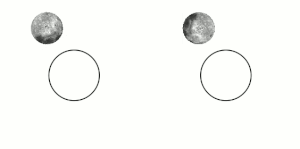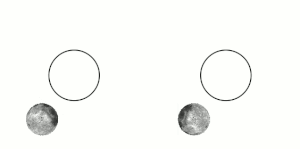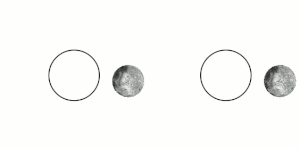
The Moon's tidal lock to Earth results in the Moon's always showing only one side to Earth (see animated image). If Earth were flat, with the Moon hovering above it, then the portion of the Moon's surface visible to people on Earth would vary according to location on Earth, rather than showing an identical "face side" to everyone. If Earth were flat, with the Moon revolving around it tidally locked, then the Moon would be seen simultaneously at all places on Earth at once, but its apparent size, the portion facing the viewer, and facing side's orientation would gradually change for each viewer as its position moved across the sky over the course of the night.

Observation of the sky from altitude with the aid of a diagram

On a perfectly spherical Earth, not considering obstructions and atmospheric refraction, its surface blocks half the sky for an observer close against the surface. Moving away from the surface of Earth means that the ground blocks less and less of the sky. For example, when viewed from the Moon, Earth blocks only a small portion of the sky because it is so distant. This effect of geometry means that, when viewed from a high mountain, flat ground or ocean blocks less than 180° of the sky. With the presumption of a spherical Earth, an expedition commissioned by caliph al-Ma'mun used this fact to calculate Earth's circumference to within 7,920 kilometres (4,920 mi) of the correct value of around 40,000 kilometres (25,000 mi), and possibly as accurately as 180 kilometres (110 mi). The rate of change in the angle blocked by Earth as altitude increases would be different for a disk than for a sphere. The amount of surface blocked would be different for a mountain close to the edge of a flat Earth compared to a mountain in the middle of a flat Earth, but this is not observed. Surveys from all over Earth show that its shape is everywhere locally convex, confirming that it is very close to spherical.

Observation of certain, fixed stars from different locations

The fixed stars, for example the Pole Star (Polaris), can be demonstrated to be very far away by diurnal parallax measurements. Such measurements show no shifts in the stars' positions. Unlike the Sun, Moon, and planets, they do not change position with respect to one another over human lifetimes; the shapes of the constellations are constant. This makes them a convenient reference background for determining the shape of Earth. Adding distance measurements on the ground allows calculation of Earth's size.

The fact that different stars are visible from different locations on Earth was noticed in ancient times. Aristotle wrote that some stars are visible from Egypt which are not visible from Europe. This would not be possible if Earth was flat.

A star has an altitude above the horizon for an observer if the star is visible. Observing the same star at the same time from two different latitudes gives two different altitudes. Using geometry, the two altitudes along with the distance between the two locations allows for a calculation of Earth's size. Using observations of the star Canopus at Rhodes (in Greece) and Alexandria (in Egypt) and the distance between them, the Ancient Greek philosopher Posidonius used this technique to calculate the circumference of the planet to within perhaps 4% of the correct value. Modern equivalents of his units of measure are not precisely known, so it is not clear how accurate his measurement was. The Spanish Muslim astronomer Ibn Rushd went to Marrakesh (in Morocco) to observe the same star in 1153, as it was invisible in his native Córdoba, Al-Andalus. He used the different visibility in different latitudes to argue that the Earth is round, following Aristotle's argument which held that such an observation was only possible if the Earth was a relatively small sphere.

Observation of constellations on North and South hemispheres at different seasons

The fact that some stars are only visible from either the north or south poles must mean that the two observation spots are on opposite sides of Earth, which is not possible if Earth is a single-sided disk, but is possible for other shapes (like a sphere, but also any other convex shape like a donut or dumbbell).

The North Pole is in continuous night for six months of the year. The star Polaris (the "North Star") is almost directly overhead and therefore at the center of this rotation. Some of the 88 modern constellations visible are Ursa Major (including the Big Dipper), Cassiopeia, and Andromeda. The other six months of the year, the North Pole is in continuous daylight, with light from the Sun blotting out the stars. This phenomenon, and its analogous effects at the South Pole, are what defines the two poles. More than 24 hours of continuous daylight can only occur north of the Arctic Circle and south of the Antarctic Circle.)

At the South Pole, a completely different set of constellations are visible during the six months of continuous night, including Crux, and Centaurus. This 180° hemisphere of stars rotates clockwise once every 24 hours around a point directly overhead.

From any point on the equator, all of the stars visible anywhere on Earth on that day are visible at some time during the year as the sky rotates around a line drawn from due north to due south. When facing east, the stars visible from the north pole are on the left, and the stars visible from the south pole are on the right.

The direction any intermediate spot on Earth is facing can also be calculated by measuring the angles of the fixed stars and determining how much of the sky is visible. For example, New York City is about 40° north of the equator. The apparent motion of the Sun blots out slightly different parts of the sky from day to day, but over the course of the entire year it sees a dome of 280° (360° - 80°). So for example, both Orion and the Big Dipper are visible during at least part of the year.

Making stellar observations from a representative set of points across Earth, combined with knowing the shortest on-the-ground distance between any two given points, makes an approximate sphere the only possible shape for Earth.

Observing the Sun

On a flat Earth, a Sun that shines in all directions would illuminate the entire surface at the same time, and all places would experience sunrise and sunset at the horizon at about the same time. With a spherical Earth, half the planet is in daylight at any given time and the other half experiences nighttime. When a given location on the spherical Earth is in sunlight, its antipode – the location exactly on the opposite side of Earth – is in darkness. The spherical shape of Earth causes the Sun to rise and set at different times in different places, and different locations get different amounts of sunlight each day.

In order to explain day and night, time zones, and the seasons, some flat Earth conjecturists propose that the Sun does not emit light in all directions, but acts more like a spotlight, only illuminating part of the flat Earth at a time. This conjecture is not consistent with observation: At sunrise and sunset, a spotlight Sun would be up in the sky at least a little bit, rather than at the horizon where it is always actually observed. A spotlight Sun would also appear at different angles in the sky with respect to a flat ground than it does with respect to a curved ground. Assuming light travels in straight lines, actual measurements of the Sun's angle in the sky from locations very distant from each other are only consistent with a geometry where the Sun is very far away and is being seen from the daylight half of a spherical Earth. These two phenomena are related: A low-altitude spotlight Sun would spend most of the day near the horizon for most locations on Earth, which is not observed, but rise and set fairly close to the horizon. A high-altitude Sun would spend more of the day away from the horizon, but rise and set fairly far from the horizon, which is also not observed.

Changing length of the day

On a flat Earth with an omnidirectional Sun, all places would experience the same amount of daylight every day, and all places would get daylight at the same time. Actual day length varies considerably, with places closer to the poles getting very long days in the summer and very short days in the winter, with northerly summer happening at the same time as southerly winter. Places north of the Arctic Circle and south of the Antarctic Circle get no sunlight for at least one day a year, and get 24-hour sunlight for at least one day a year. Both the poles experience sunlight for 6 months and darkness for 6 months, at opposite times.

The movement of daylight between the northern and southern hemispheres happens because of the axial tilt of Earth. The imaginary line around which Earth spins, which goes between the North Pole and South Pole, is tilted about 23° from the oval that describes its orbit around the Sun. Earth always points in the same direction as it moves around the Sun, so for half the year (summer in the Northern Hemisphere), the North Pole is pointed slightly toward the Sun, keeping it in daylight all the time because the Sun lights up the half of Earth that is facing it (and the North Pole is always in that half due to the tilt). For the other half of the orbit, the South Pole is tilted slightly toward the Sun, and it is winter in the Northern Hemisphere. This means that at the equator, the Sun is not directly overhead at noon, except around the March and September equinoxes, when one spot on the equator is pointed directly at the Sun.

Length of the day beyond polar circles

The length of the day varies because as Earth rotates, some places (near the poles) pass through only a short curve near the top or bottom of the sunlight half; other places (near the equator) travel along much longer curves through the middle. In locations just outside the polar circles, there are so-called "white nights" in the middle of summer, in which the sun is never more than a few degrees below the horizon in June such that a bright twilight persists from sunset to sunrise. In Russia, Saint Petersburg uses this phenomenon in its tourist marketing.

Length of the twilight

Longer twilights are observed at higher latitudes (near the poles) due to a shallower angle of the Sun's apparent movement compared to the horizon. On a flat Earth, the Sun's shadow would reach the upper atmosphere very quickly, except near the closest edge of Earth, and would always set at the same angle to the ground (which is not what is observed).

The length of twilight would be very different on a flat Earth. On a round Earth, the atmosphere above the ground is lit for a while before sunrise and after sunset are observed at ground level, because the Sun is still visible from higher altitudes.

The "spotlight Sun" conjecture is also not consistent with this observation, since the air cannot be lit without the ground below it also being lit (except for shadows of mountains, hi-rises and other surface obstacles).

Observing sunlight before or after seeing Sun

It is possible to see sun-lit windows of nearby high-rise buildings from ground level a few minutes before seeing the sun rise or after seeing the sun set. On a non-curved, flat landmass it would only take seconds, due to minuscule ratio (compare ~45 meters / 150 feet of a 14-story building to intercontinental distances). If such a phenomenon were caused by a prismatic property of atmosphere in a flat world, with a relatively small source of light revolving around Earth (as in later, 1800's-dated, maps of Flat Earth), it would contradict with one's ability to see a proper panorama of starry sky at a time at night, rather than a small yet distorted, "stretched" patch of it. Likewise, the top of a mountain is illuminated before sunrise and after sunset, as are clouds.

Watching the sun set twice

On level ground, the difference in the distance to the horizon between lying down and standing up is large enough to watch the Sun set twice by quickly standing up immediately after seeing it set for the first time while lying down. This also can be done with an aerial work platform or with a fast elevator. On a flat Earth or a significantly large flat segment, it would not be possible to see the Sun again (unless standing near the edge closest to the Sun) due to a much faster-moving Sun shadow.

Local solar time and time zones

Main article: Time zone

Ancient timekeeping reckoned "noon" as the time of day when the Sun is highest in the sky, with the rest of the hours in the day measured against that. During the day, the apparent solar time can be measured directly with a sundial. In ancient Egypt, the first known sundials divided the day into 12 hours, though because the length of the day changed with the season, the length of the hours also changed. Sundials that defined hours as always being the same duration appeared in the Renaissance. In Western Europe, clock towers and striking clocks were used in the Middle Ages to keep people nearby appraised of the local time, though compared to modern times this was less important in a largely agrarian society.

Because the Sun reaches its highest point at different times for different longitudes (about four minutes of time for every degree of longitude difference east or west), the local solar noon in each city is different except for those directly north or south of each other. This means that the clocks in different cities could be offset from each other by minutes or hours. As clocks became more precise and industrialization made timekeeping more important, cities switched to mean solar time, which ignores minor variations in the timing of local solar noon over the year, due to the elliptical nature of Earth's orbit, and its tilt.

The differences in clock time between cities was not generally a problem until the advent of railroad travel in the 1800s, which both made travel between distant cities much faster than by walking or horse, and also required passengers to show up at specific times to meet their desired trains. In the United Kingdom, railroads gradually switched to Greenwich Mean Time (set from local time at the Greenwich observatory in London), followed by public clocks across the country generally, forming a single time zone. In the United States, railroads published schedules based on local time, then later based on standard time for that railroad (typically the local time at the railroad's headquarters), and then finally based on four standard time zones shared across all railroads, where neighboring zones differed by exactly one hour. At first railroad time was synchronized by portable chronometers, and then later by telegraph and radio signals.

San Francisco is at 122.41°W longitude and Richmond, Virginia is at 77.46°W longitude. They are both at about 37.6°N latitude (±.2°). The approximately 45° of longitude difference translates into about 180 minutes, or 3 hours, of time between sunsets in the two cities, for example. San Francisco is in the Pacific Time zone, and Richmond is in the Eastern Time zone, which are three hours apart, so the local clocks in each city show that the Sun sets at about the same time when using the local time zone. But a phone call from Richmond to San Francisco at sunset will reveal that there are still three hours of daylight left in California.

Determining the size of Earth by Eratosthenes

Sunbeams are shown as two rays hitting the ground at Syene and Alexandria. The angle between the sunbeam and a gnomon (vertical pole) at Alexandria allowed Eratosthenes to estimate Earth's circumference

Under the assumption that the Sun is very far away, the ancient Greek geographer Eratosthenes performed an experiment using the differences in the observed angle of the Sun from two different locations to calculate the circumference of Earth. Though modern telecommunications and timekeeping were not available, he was able to make sure the measurements happened at the same time by having them taken when the Sun was highest in the sky (local noon) at both locations. Using slightly inaccurate assumptions about the locations of two cities, he came to a result within 15% of the correct value. While his results could theoretically also be compatible with a Flat Earth if the light rays from the Sun are assumed not to be parallel, many people have repeated the experiment with three or more data points and found results unambiguously supporting the globe model.

Angle to the Sun at different locations

On a given day, if many different cities measure the angle of the Sun at local noon, the resulting data, when combined with the known distances between cities, shows that Earth has 180 degrees of north-south curvature. (A full range of angles will be observed if the north and south poles are included, and the day chosen is either the autumnal or spring equinox.) This is consistent with many rounded shapes, including a sphere, and is inconsistent with a flat shape.

Some claim that this experiment assumes a very distant Sun, such that the incoming rays are essentially parallel, and if a flat Earth is assumed, that the measured angles can allow one to calculate the distance to the Sun, which must be small enough that its incoming rays are not very parallel. However, if more than two relatively well-separated cities are included in the experiment, the calculation will make clear whether the Sun is distant or nearby. For example, on the equinox, the 0 degree angle from the North Pole and the 90 degree angle from the equator predict a Sun which would have to be located essentially next to the surface of a flat Earth, but the difference in angle between the equator and New York City would predict a Sun much further away if Earth is flat. Because these results are contradictory, the surface of Earth cannot be flat; the data are, instead, consistent with a nearly spherical Earth and a Sun which is very far away compared with the diameter of Earth.

Surface navigation

The first circumnavigation of the Earth by the Magellan expedition lost a day, confirmed by subsequent circumnavigations, which eventually led to the creation of the International Date Line.

The shortest way to travel between two distant points is by great circle navigation, as known by ocean navigators for some time. This route shows as curved on any map except for one using a gnomonic projection. Radio waves also follow a great circle, so navies have produced maps using gnomonic projection for use in radio direction finding to locate enemy warships.

Since the 1500s, many people have sailed or flown completely around Earth in all directions, and none have discovered an edge or impenetrable barrier. (See Arctic exploration and History of Antarctica.)

Some flat Earth conjectures that propose that Earth is a north-pole-centered disk conceive of Antarctica as an impenetrable ice wall that encircles the planet and hides any edges. This disk model explains east-west circumnavigation as simply moving around the disk in a circle. (East-west paths form a circle in both disk and spherical geometry.) It is possible in this model to traverse the North Pole, but it would not be possible to perform a circumnavigation that includes the South Pole (which it posits does not exist).

The Arctic Circle is roughly 16,000 km (9,900 mi) long, as is the Antarctic Circle. A "true circumnavigation" of Earth is defined, in order to account for the shape of Earth, to be about 2.5 times as long, including a crossing of the equator, at about 40,000 km (25,000 mi). On the flat Earth model, the ratios would require the Antarctic Circle to be 2.5 times the length of the circumnavigation, or 2.5 × 2.5 = 6.25 times the length of the Arctic Circle.

Explorers, government researchers, commercial pilots, and tourists have been to Antarctica and found that it is not a large ring that encircles the entirety of Earth, but actually a roughly disk-shaped continent smaller than South America but larger than Australia, with an interior that can in fact be traversed in order to take a shorter path from, for example, the tip of South America to Australia than would be possible on a disk.

The first land crossing of the entirety of Antarctica was the Commonwealth Trans-Antarctic Expedition in 1955–1958, and many exploratory airplanes have since passed over the continent in various directions.

Grid distortion on a spherical surface

A meridian of longitude is a line where local solar noon occurs at the same time each day. These lines define "north" and "south". These are perpendicular to lines of latitude that define "east" and "west", where the Sun is at the same angle at local noon on the same day. If the Sun were travelling from east to west over a flat Earth, meridian lines would always be the same distance apart – they would form a square grid when combined with lines of latitude. In reality, meridian lines get farther apart as one travels toward the equator, which is only possible on a round Earth. In places where land is plotted on a grid system, this causes discontinuities in the grid. For example, in areas of the Midwestern United States that use the Public Land Survey System, the northernmost and westernmost sections of a survey township deviate from what would otherwise be an exact square mile. The resulting discontinuities are sometimes reflected directly in local roads, which have kinks where the grid cannot follow completely straight lines. This distortion also affects how aerial photographs taken over large areas can be stitched together.

The Mercator projection has examples of size distortions.

Spherical versus flat triangles

Diagram showing how the interior angles of triangles add up to about 180° when plotted on a small, nearly flat area of Earth, but add up to more than 180° (in this case 230°) when plotted on a large area with significant curvature

Because Earth is spherical, long-distance travel sometimes requires heading in different directions than one would head on a flat Earth. An example would be an airplane travelling 10,000 kilometres (6,200 mi) in a straight line, taking a 90-degree right turn, travelling another 10,000 kilometres (6,200 mi), taking another 90-degree right turn, and travelling 10,000 kilometres (6,200 mi) a third time. On a flat Earth, the aircraft would have travelled along three sides of a square, and arrive at a spot about 10,000 kilometres (6,200 mi) from where it started. But because Earth is spherical, in reality it will have travelled along three sides of a triangle, and arrive back very close to its starting point. If the starting point is the North Pole, it would have travelled due south from the North Pole to the equator, then west for a quarter of the way around Earth, and then due north back to the North Pole.

In spherical geometry, the sum of angles inside a triangle is greater than 180° (in this example 270°, having arrived back at the north pole a 90° angle to the departure path) unlike on a flat surface, where it is always exactly 180°.

Weather systems

Low-pressure weather systems with inward winds (such as a hurricane) spin counterclockwise north of the equator, but clockwise south of the equator. This is due to the Coriolis force, and requires that (assuming they are attached to each other and rotating in the same direction) the north and southern halves of Earth are angled in opposite directions (as in, the north is facing toward Polaris and the south is facing away from it).

Gravity

The laws of gravity, chemistry, and physics that explain the formation and rounding of Earth are well-tested through experiment, and applied successfully to many engineering tasks.

From these laws, the amount of mass Earth contains is known, as is the fact that a non-spherical planet the size of Earth would not be able to support itself against its own gravity. A disk the size of Earth, for example, would likely crack, heat up, liquefy, and re-form into a roughly spherical shape. On a disk strong enough to maintain its shape, gravity would not pull downward with respect to the surface, but would pull toward the center of the disk, contrary to what is observed on level terrain (and which would cause major problems with oceans flowing toward the center of the disk).

Ignoring the other concerns, some flat Earth conjecturists explain the observed surface "gravity" by proposing that the flat Earth is constantly accelerating upwards. Such a conjecture would also leave open for explanation the tides seen in Earth's oceans, which are conventionally explained by the gravity exerted by the Sun and Moon. The Earth would also quickly approach light-speed in this scenario because the pull of gravity would increase by -9.8m/s, each second (as the formula for gravitational acceleration is measured in m/s²).

Modern technology

Observations of Foucault pendulums, popular in science museums around the world, demonstrate both that the world is spherical and that it rotates (not that the stars are rotating around it).

The mathematics of navigation using Global Positioning System (GPS) satellites assumes that they are moving in known orbits around an approximately spherical surface. The accuracy of GPS navigation in determining latitude and longitude and the way these numbers map onto locations on the ground show that these assumptions are correct. The same is true for the operational GLONASS system run by Russia, the in-development European Galileo, the Chinese BeiDou, and the Indian Regional Navigation Satellite System.

Satellites, including communications satellites used for television, telephone, and Internet connections, would not stay in orbit unless the modern theory of gravitation were correct. The details of which satellites are visible from which places on the ground at which times prove an approximately spherical shape of Earth.

Radio transmitters are mounted on tall towers because they generally rely on line-of-sight propagation. The distance to the horizon is further at higher altitude, so mounting them higher significantly increases the area they can serve. Some signals can be transmitted at much longer distances, but only if they are at frequencies where they can use groundwave propagation, tropospheric propagation, tropospheric scatter, or ionospheric propagation to reflect or refract signals around the curve of Earth.

Equatorial mounts allow astronomers to point telescopes at the same celestial object for longer times while compensating for Earth's rotation in an easy way. The axis of an equatorial mount is parallel to Earth's surface when observing stars at Earth's equator – but perpendicular to it when observing from one of Earth's poles. Equatorial mounts were specifically developed for a spherical and rotating Earth. If Earth were flat, an equatorial mount would not make sense.

Building engineering

The design of some large structures needs to take the shape of Earth into account. For example, the towers of the Humber Bridge, although both vertical with respect to gravity, are 36 mm (1.4 inches) farther apart at the top than the bottom due to Earth's curvature.

Aircraft and spacecraft

People in high-flying aircraft or skydiving from high-altitude balloons can plainly see the curvature of Earth. Low-flying planes and commercial airliners do not necessarily fly high enough to make this obvious, especially when passenger windows narrow the field of view or clouds or terrain reduce the effective height from the visible surface. Trying to measure the curvature of the horizon by taking a picture is complicated by the fact that both windows and camera lenses can produce distorted images depending on the angle used. An extreme version of this effect can be seen in the fisheye lens. Scientific measurements would require a carefully calibrated lens.

Photos of the ground taken from airplanes over a large enough area also do not fit seamlessly together on a flat surface, but do fit on a roughly spherical surface. Aerial photographs of large areas must be corrected to account for curvature.

Many pictures have been taken of the entirety of Earth by satellites launched by a variety of governments and private organizations. From high orbits, where half the planet can be seen at once, it is plainly spherical. The only way to piece together all the pictures taken of the ground from lower orbits so that all the surface features line up seamlessly and without distortion is to put them on an approximately spherical surface.

Astronauts in low Earth orbit can personally see the curvature of the planet, and travel all the way around several times a day. The astronauts who travelled to the Moon have seen the entire Moon-facing half at once, and can watch the sphere rotate once a day (approximately; the Moon is also moving with respect to Earth).

When the supersonic aircraft Concorde took off not long after sunset from London and flew westward to New York, it outran the Sun's apparent motion westward – and therefore passengers aboard observed the Sun rising in the west as they travelled. After landing in New York, passengers watched a second sunset in the west.

Plot of latitude vs tangential speed. The dashed line shows the Kennedy Space Center example. The dot-dash line denotes typical airliner cruise speed.

Because the speed of the Sun's shadow is slower in polar regions (due to the steeper angle), even a subsonic aircraft can overtake the sunset when flying at high latitudes. One photographer used a roughly circular route around the North Pole to take pictures of 24 sunsets in the same 24-hour period, pausing westward progress in each time zone to let the shadow of the Sun catch up. The surface of Earth rotates at 180.17 miles per hour (289.96 km/h) at 80° north or south, and 1,040.4 miles per hour (1,674.4 km/h) at the equator.

Ring-Laser Gyroscope

In the Flat Earth documentary Behind the Curve, Bob Knodel uses a ring-laser gyroscope to prove that the earth does not rotate, but the results showed a 15 degree per hour drift, due to the earth's rotation.