Jump to content

Fractal

From Wikipedia, the free encyclopedia

This is an old revision of this page, as edited by Gandalf61 (talk | contribs) at 09:29, 10 July 2004 (→‎History: Link). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

A closeup of the Mandelbrot set, the most famous fractal.

A fractal is a mathematical function or geometric shape that is self-similar on all scales. The concept of a fractal originated as a strictly mathematical idea, but has come to be used as a scientific concept as well. Informally, a fractal can be understood as an object that always looks the same, or at least similar, no matter how much it is magnified. The word fractal was coined in 1975 by Benoit Mandelbrot.

History

Koch snowflake

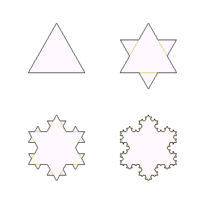
Objects that we now call fractals were discovered and explored long before we had a word for them. In 1872 Karl Weierstrass found an example of a function with the non-intuitive property that it is everywhere continuous but nowhere differentiable - the graph of this function would now be called a fractal. In 1904 Helge von Koch, dissatisfied with Weierstrass's very abstract and analytic definition, gave a more geometric definition of a similar function, which is now called the Koch snowflake. The idea of self-similar curves was taken further by Paul Pierre Lévy who, in his 1938 paper Plane or Space Curves and Surfaces Consisting of Parts Similar to the Whole, described two fractal curves, the Lévy C curve and the Lévy dragon curve.

Georg Cantor gave examples of subsets of the real line with unusual properties - these Cantor sets are also now recognised as fractals. In an attempt to understand objects such as Cantor sets, mathematicians such as Constantin Carathéodory and Felix Hausdorff generalised the intuitive concept of dimension to include non-integer values. Iterated functions in the complex plane had been investigated in the late 19th and early 20th centuries by Henri Poincaré, Felix Klein, Pierre Fatou and Gaston Julia. However, without the aid of modern computer graphics, they lacked the means to visualise the beauty of the objects that they had discovered.

In the 1960s Benoit Mandelbrot started investigating self-similarity in papers such as How Long Is the Coast of Britain ? Statistical Self-Similarity and Fractional Dimension (see below). Taking a highly visual approach, Mandelbrot recognised connections between these previously unrelated strands of mathematics. In 1975 Mandelbrot coined the word fractal to describe self-similar objects. He derived the word fractal from the Latin fractus, meaning broken or irregular.

How Long is the Coast of Britain?

Lewis Fry Richardson was a pacifist and a mathematician, studying the cause of war between two countries. He decided to search for a relation between the size of its mutual border and the probability of two countries entering a war. As part of this research, he investigated how the measured length of a border changes as the unit of measurement is changed. Richardson published empirical statistics which led to a conjectured relationship. This research was quoted by Mandelbrot in his 1967 paper How Long Is the Coast of Britain?.

Suppose you try to measure Britain's coast using a 200 km ruler, specifying that both ends of the ruler must touch the coast. Then you cut the ruler in half, and again:

File:Britain-fractal-coastline-200km.jpg File:Britain-fractal-coastline-100km.jpg File:Britain-fractal-coastline-50km.jpg

The interesting part here is that the smaller the ruler, the bigger result you get. One might suppose that these values would tend to a finite number representing the "true" length of the coastline, but Richardson proved that the measurements of the coastline actually tended to infinity.

File:How-long.jpg

At the time Richardson's research was ignored by the scientific community. Today, many see it as one element of the birth of the modern study of fractals.

Categories of fractals

1
2
3
4 Self-similarity in the Mandelbrot set. The top image is the full set, and each subsequent image is a closeup of the red square.

Fractals can be grouped into three broad categories:

Of all these, only iterated function systems usually display the well-known "self-similarity" property--meaning that their complexity is invariant under scaling transforms. Fractals such as the Mandelbrot set are more loosely self-similar: they contain small copies of the entire fractal in distorted and degenerate forms.

Because a fractal is defined as self-similar at all scales, no natural object can be a fractal. However, natural objects can display fractal properties across a limited range of scales.

Definitions

The secondary characteristics of fractals, while intuitively appealing, are remarkably hard to condense into a mathematically precise definition. Strictly, a fractal should have fractional (that is, noninteger) Hausdorff (or box-counting) dimension. There are objects that have the appearance of fractals but which do not satisfy this definition.

Problems with defining fractals include:

  • There is no precise meaning of "too irregular"
  • There are many ways that an object can be self-similar
  • Not every fractal is defined recursively

The many definitions of dimension giving fractional values do not always agree numerically, so an acceptable definition of fractal cannot be based on a single fractal dimension.

Examples

A natural fractal formed by pulling two glue-covered acrylic sheets apart.

Trees and ferns are fractal in nature and can be modelled on a computer using a recursive algorithm. This recursive nature is clear in these examples — take a branch from a tree or a frond from a fern and you will see it is a miniature replica of the whole. Not identical, but similar in nature.

A relatively simple class of examples is the Cantor sets, in which short and then shorter (open) intervals are struck out of the unit interval [0,1], leaving a set that might (or might not) actually be self-similar under enlargement, and might (or might not) have dimension d that has 0 < d < 1. A simple recipe, such as excluding the digit 7 from decimal expansions, is self-similar under 10-fold enlargement, and also has dimension log 9/log 10, showing the connection of the two concepts.

Fractals are generally irregular (not smooth) in shape, and thus are not objects definable by traditional geometry. That means that fractals tend to have significant detail, visible at any arbitrary scale; when there is self-similarity, this can occur because 'zooming in' simply shows similar pictures. Such sets are usually defined instead by recursion.

For example, a normal Euclidean shape, such as a circle, looks flatter and flatter as it is magnified. At infinite magnification it is impossible to tell the difference between a circle and a straight line. Fractals are not like this. The conventional idea of curvature, which represents the reciprocal of the radius of an approximating circle, cannot usefully apply because it scales away. Instead, in a fractal, increasing the magnification reveals detail that you simply couldn't see before.

Some common examples of fractals include the Mandelbrot set, Lyapunov fractal, Cantor set, Sierpinski carpet and triangle, Peano curve and the Koch snowflake. Fractals can be deterministic or stochastic. Chaotic dynamical systems are often (if not always) associated with fractals. The celebrated Mandelbrot set contains whole discs, so has dimension 2.

Approximate fractals are easily found in nature. These objects display complex structure over an extended, but finite, scale range. These naturally occurring fractals (like clouds, mountains, river networks, and systems of blood vessels) have both lower and upper cut-offs, but they are separated by several orders of magnitude. Despite being ubiquitous, fractals were not much studied until well into the twentieth century, and general definitions came later.

File:Fractal juliaset holes.png
One of the Julia sets.

Harrison extended Newtonian calculus to fractal domains, including the theorems of Gauss, Green, and Stokes.

Fractals are usually calculated by computers with fractal software. See below for a list.

Random fractals have the greatest practical use because they can be used to describe many highly irregular real-world objects. Examples include clouds, mountains, turbulence, coastlines and trees. Fractal techniques have also been employed in fractal image compression, as well as a variety of scientific disciplines.

See also

References, further reading

  • 1 Fractal Geometry, by Kenneth Falconer; John Wiley & Son Ltd; ISBN 0471922870 (March 1990)
  • The Fractal Geometry of Nature, by Benoit Mandelbrot; W H Freeman & Co; ISBN 0716711869 (hardcover, September 1982).
  • The Science of Fractal Images, by Heinz-Otto Peitgen, Dietmar Saupe (Editor); Springer Verlag; ISBN 0387966080 (hardcover, August 1988)
  • Fractals Everywhere, by Michael F. Barnsley; Morgan Kaufmann; ISBN 0120790610

Fractal generators

 

Retrieved from "https://en.wikipedia.org/w/index.php?title=Fractal&oldid=4548872"