Metaheuristic
In computer science, metaheuristic designates a computational method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality. Metaheuristics make few or no assumptions about the problem being optimized and can search very large spaces of candidate solutions. However, metaheuristics do not guarantee an optimal solution is ever found. Many metaheuristics implement some form of stochastic optimization.
Other terms having a similar meaning as metaheuristic, are: direct search, black-box, or indeed just heuristic optimizer. Several books and survey papers have been published on the subject.[1][2][3][4]
In a 2013 article in the International Transactions in Operational Research Kenneth Sörensen, professor of operations research at the University of Antwerp, stated critically:[5]
In recent years, the field of combinatorial optimization has witnessed a true tsunami of "novel" metaheuristic methods, most of them based on a metaphor of some natural or man-made process. The behavior of virtually any species of insects, the flow of water, musicians playing together – it seems that no idea is too far-fetched to serve as inspiration to launch yet another metaheuristic. In this paper, we will argue that this line of research is threatening to lead the area of metaheuristics away from scientific rigor. [...] At the same time, truly innovative research of high quality is being performed as well.
Applications
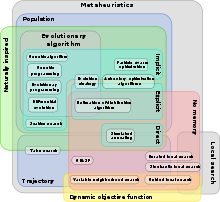
Metaheuristics are used for combinatorial optimization in which an optimal solution is sought over a discrete search-space. An example problem is the travelling salesman problem where the search-space of candidate solutions grows faster than exponentially as the size of the problem increases, which makes an exhaustive search for the optimal solution infeasible. Additionally, multidimensional combinatorial problems, including most design problems in engineering such as form-finding and behavior-finding, suffer from the curse of dimensionality, which also makes them infeasible for exhaustive search or analytical methods. Popular metaheuristics for combinatorial problems include simulated annealing by Kirkpatrick et al.,[6] genetic algorithms by Holland et al.,[7] scatter search[8] and tabu search[9] by Glover. Literature review on metaheuristic optimization,[10] suggested that it was Fred Glover who coined the word metaheuristics [11]
Contributions
Many different metaheuristics are in existence and new variants are continually being proposed. Some of the most significant contributions to the field are:
- 1952: Robbins and Monro work on stochastic optimization methods.[12]
- 1954: Barricelli carry out the first simulations of the evolution process and use them on general optimization problems.[13]
- 1963: Rastrigin proposes random search.[14]
- 1965: Matyas proposes random optimization.[15]
- 1965: Nelder and Mead propose a simplex heuristic, which was shown by Powell to converge to non-stationary points on some problems.[16]
- 1966: Fogel et al. propose evolutionary programming.[17]
- 1970: Hastings proposes the Metropolis-Hastings algorithm.[18]
- 1970: Cavicchio proposes adaptation of control parameters for an optimizer.[19]
- 1970: Kernighan and Lin propose a graph partitioning method, related to variable-depth search and prohibition-based (tabu) search.[20]
- 1975: Holland proposes the genetic algorithm.[7]
- 1977: Glover proposes Scatter Search.[8]
- 1978: Mercer and Sampson propose a metaplan for tuning an optimizer's parameters by using another optimizer.[21]
- 1980: Smith describes genetic programming.[22]
- 1983: Kirkpatrick et al. propose simulated annealing.[6]
- 1986: Glover proposes tabu search, first mention of the term metaheuristic.[9]
See also
- Stochastic search
- Meta-optimization
- Matheuristics
- List of metaheuristics
- Hyper-heuristics
- Swarm intelligence
References
- ^ Goldberg, D.E. (1989). Genetic Algorithms in Search, Optimization and Machine Learning. Kluwer Academic Publishers. ISBN 0-201-15767-5.
- ^ Glover, F.; Kochenberger, G.A. (2003). Handbook of metaheuristics. Vol. 57. Springer, International Series in Operations Research & Management Science. ISBN 978-1-4020-7263-5.
- ^
Blum, C.; Roli, A. (2003). "Metaheuristics in combinatorial optimization: Overview and conceptual comparison". 35 (3). ACM Computing Surveys: 268–308.
{{cite journal}}: Cite journal requires|journal=(help) - ^ Talbi, E-G. (2009). Metaheuristics: from design to implementation. Wiley. ISBN 0-470-27858-7.
- ^ Sörensen, Kenneth. "Metaheuristics—the metaphor exposed" (PDF). International Transactions in Operational Research. doi:10.1111/itor.12001.
- ^ a b Kirkpatrick, S.; Gelatt Jr., C.D.; Vecchi, M.P. (1983). "Optimization by Simulated Annealing". Science. 220 (4598): 671–680. doi:10.1126/science.220.4598.671. PMID 17813860.
- ^ a b Holland, J.H. (1975). Adaptation in Natural and Artificial Systems. University of Michigan Press. ISBN 0-262-08213-6.
- ^ a b Glover, Fred (1977). "Heuristics for Integer programming Using Surrogate Constraints". Decision Sciences. 8 (1): 156–166.
- ^ a b Glover, F. (1986). "Future Paths for Integer Programming and Links to Artificial Intelligence". Computers and Operations Research. 13 (5): 533–549. doi:10.1016/0305-0548(86)90048-1.
- ^ X. S. Yang, Metaheuristic optimization, Scholarpedia, 6(8):11472 (2011).
- ^ Glover F., (1986). Future paths for integer programming and links to artificial intelligence, Computers and Operations Research,13,533-549 (1986).
- ^ Robbins, H.; Monro, S. (1951). "A Stochastic Approximation Method". Annals of Mathematical Statistics. 22 (3): 400–407. doi:10.1214/aoms/1177729586.
- ^ Barricelli, N.A. (1954). "Esempi numerici di processi di evoluzione". Methodos: 45–68.
- ^ Rastrigin, L.A. (1963). "The convergence of the random search method in the extremal control of a many parameter system". Automation and Remote Control. 24 (10): 1337–1342.
- ^ Matyas, J. (1965). "Random optimization". Automation and Remote Control. 26 (2): 246–253.
- ^ Nelder, J.A.; Mead, R. (1965). "A simplex method for function minimization". Computer Journal. 7: 308–313. doi:10.1093/comjnl/7.4.308.
- ^ Fogel, L.; Owens, A.J.; Walsh, M.J. (1966). Artificial Intelligence through Simulated Evolution. Wiley. ISBN 0-471-26516-0.
- ^ Hastings, W.K. (1970). "Monte Carlo Sampling Methods Using Markov Chains and Their Applications". Biometrika. 57 (1): 97–109. doi:10.1093/biomet/57.1.97.
- ^ Cavicchio, D.J. (1970). "Adaptive search using simulated evolution". Technical Report. University of Michigan, Computer and Communication Sciences Department. hdl:2027.42/4042.
- ^
Kernighan, B.W.;Lin, S. (1970). "An efficient heuristic procedure for partitioning graphs". Bell System Technical Journal. 49 (2): 291–307.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^
Mercer, R.E. (1978). "Adaptive search using a reproductive metaplan". Kybernetes (The International Journal of Systems and Cybernetics). 7 (3): 215–228. doi:10.1108/eb005486.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ Smith, S.F. (1980). A Learning System Based on Genetic Adaptive Algorithms (PhD Thesis). University of Pittsburgh.
External links
- EU/ME forum for researchers in the field.
- MetaHeur - Excel application to metaheuristic methods
Template:Metaheuristics for combinatorial problems Template:Metaheuristics for real-valued problems

