Activation function

For the formalism used to approximate the influence of an extracellular electrical field on neurons, see activating function. For a linear system’s transfer function, see transfer function.

Logistic activation function

In artificial neural networks, the activation function of a node defines the output of that node given an input or set of inputs. A standard computer chip circuit can be seen as a digital network of activation functions that can be "ON" (1) or "OFF" (0), depending on input. This is similar to the behavior of the linear perceptron in neural networks. However, only nonlinear activation functions allow such networks to compute nontrivial problems using only a small number of nodes. In artificial neural networks this function is also called the transfer function.

Functions

In biologically inspired neural networks, the activation function is usually an abstraction representing the rate of action potential firing in the cell. In its simplest form, this function is binary—that is, either the neuron is firing or not. The function looks like $\phi (v_{i})=U(v_{i})$, where $U$ is the Heaviside step function. In this case many neurons must be used in computation beyond linear separation of categories.

A line of positive slope may be used to reflect the increase in firing rate that occurs as input current increases. Such a function would be of the form $\phi (v_{i})=\mu v_{i}$, where $\mu$ is the slope. This activation function is linear, and therefore has the same problems as the binary function. In addition, networks constructed using this model have unstable convergence because neuron inputs along favored paths tend to increase without bound, as this function is not normalizable.

All problems mentioned above can be handled by using a normalizable sigmoid activation function. One realistic model stays at zero until input current is received, at which point the firing frequency increases quickly at first, but gradually approaches an asymptote at 100% firing rate. Mathematically, this looks like $\phi (v_{i})=U(v_{i})\tanh(v_{i})$, where the hyperbolic tangent function can be replaced by any sigmoid function. This behavior is realistically reflected in the neuron, as neurons cannot physically fire faster than a certain rate. This model runs into problems, however, in computational networks as it is not differentiable, a requirement to calculate backpropagation.

The final model, then, that is used in multilayer perceptrons is a sigmoidal activation function in the form of a hyperbolic tangent. Two forms of this function are commonly used: $\phi (v_{i})=\tanh(v_{i})$ whose range is normalized from -1 to 1, and $\phi (v_{i})=(1+\exp(-v_{i}))^{-1}$ is vertically translated to normalize from 0 to 1. The latter model is often considered more biologically realistic, but it runs into theoretical and experimental difficulties with certain types of computational problems.

Alternative structures

A special class of activation functions known as radial basis functions (RBFs) are used in RBF networks, which are extremely efficient as universal function approximators. These activation functions can take many forms, but they are usually found as one of three functions:

• Gaussian: $\,\phi (v_{i})=\exp \left(-{\frac {\|v_{i}-c_{i}\|^{2}}{2\sigma ^{2}}}\right)$
• Multiquadratics: $\,\phi (v_{i})={\sqrt {\|v_{i}-c_{i}\|^{2}+a^{2}}}$
• Inverse multiquadratics: $\,\phi (v_{i})=(\|v_{i}-c_{i}\|^{2}+a^{2})^{-1/2}$

where $c_{i}$ is the vector representing the function center and $a$ and $\sigma$ are parameters affecting the spread of the radius.

Support vector machines (SVMs) can effectively utilize a class of activation functions that includes both sigmoids and RBFs. In this case, the input is transformed to reflect a decision boundary hyperplane based on a few training inputs called support vectors $x$. The activation function for the hidden layer of these machines is referred to as the inner product kernel, $K(v_{i},x)=\phi (v_{i})$. The support vectors are represented as the centers in RBFs with the kernel equal to the activation function, but they take a unique form in the perceptron as

$\,\phi (v_{i})=\tanh \left(\beta _{1}+\beta _{0}\sum _{j}v_{i,j}x_{j}\right)$,

where $\beta _{0}$ and $\beta _{1}$ must satisfy certain conditions for convergence. These machines can also accept arbitrary-order polynomial activation functions where

$\,\phi (v_{i})=\left(1+\sum _{j}v_{i,j}x_{j}\right)^{p}$.

Activation function having types:

• Identity function
• Binary step function
• Bipolar step function
• Sigmoidal function
  • Binary sigmoidal function
  • Bipolar sigmoidal function
• Ramp function

Comparison of activation functions

Some desirable properties in an activation function include:

• Nonlinear – When the activation function is non-linear, then a two-layer neural network can be proven to be a universal function approximator. The identity activation function does not satisfy this property. When multiple layers use the identity activation function, the entire network is equivalent to a single-layer model.
• Continuously differentiable – This property is desirable (RELU is not continuously differentiable and has some issues with gradient-based optimization, but it is still possible) for enabling gradient-based optimization methods. The binary step activation function is not differentiable at 0, and it differentiates to 0 for all other values, so gradient-based methods can make no progress with it.
• Range – When the range of the activation function is finite, gradient-based training methods tend to be more stable, because pattern presentations significantly affect only limited weights. When the range is infinite, training is generally more efficient because pattern presentations significantly affect most of the weights. In the latter case, smaller learning rates are typically necessary.
• Monotonic – When the activation function is monotonic, the error surface associated with a single-layer model is guaranteed to be convex.
• Smooth Functions with a Monotonic derivative – These have been shown to generalize better in some cases.
• Approximates identity near the origin – When activation functions have this property, the neural network will learn efficiently when its weights are initialized with small random values. When the activation function does not approximate identity near the origin, special care must be used when initializing the weights. In the table below, activation functions where $f(0)=0$ and $f'(0)=1$ and $f'$ is continuous at 0 are indicated as having this property.

The following table compares the properties of several activation functions that are functions of one fold x from the previous layer or layers:

Name	Plot	Equation	Derivative (with respect to x)	Range	Order of continuity	Monotonic	Derivative Monotonic	Approximates identity near the origin
Identity		$f(x)=x$	$f'(x)=1$	$(-\infty ,\infty )$	$C^{\infty }$	Yes	Yes	Yes
Binary step		$f(x)={\begin{cases}0&{\text{for }}x<0\\1&{\text{for }}x\geq 0\end{cases}}$	$f'(x)={\begin{cases}0&{\text{for }}x\neq 0\\?&{\text{for }}x=0\end{cases}}$	$\{0,1\}$	$C^{-1}$	Yes	No	No
Logistic (a.k.a. Sigmoid or Soft step)		$f(x)=\sigma (x)={\frac {1}{1+e^{-x}}}$[1]	$f'(x)=f(x)(1-f(x))$	$(0,1)$	$C^{\infty }$	Yes	No	No
TanH		$f(x)=\tanh(x)={\frac {(e^{x}-e^{-x})}{(e^{x}+e^{-x})}}$	$f'(x)=1-f(x)^{2}$	$(-1,1)$	$C^{\infty }$	Yes	No	Yes
ArcTan		$f(x)=\tan ^{-1}(x)$	$f'(x)={\frac {1}{x^{2}+1}}$	$\left(-{\frac {\pi }{2}},{\frac {\pi }{2}}\right)$	$C^{\infty }$	Yes	No	Yes
Softsign		$f(x)={\frac {x}{1+|x|}}$	$f'(x)={\frac {1}{(1+|x|)^{2}}}$	$(-1,1)$	$C^{1}$	Yes	No	Yes
Inverse square root unit (ISRU)		$f(x)={\frac {x}{\sqrt {1+\alpha x^{2}}}}$	$f'(x)=\left({\frac {1}{\sqrt {1+\alpha x^{2}}}}\right)^{3}$	$\left(-{\frac {1}{\sqrt {\alpha }}},{\frac {1}{\sqrt {\alpha }}}\right)$	$C^{\infty }$	Yes	No	Yes
Rectified linear unit (ReLU)		$f(x)={\begin{cases}0&{\text{for }}x<0\\x&{\text{for }}x\geq 0\end{cases}}$	$f'(x)={\begin{cases}0&{\text{for }}x<0\\1&{\text{for }}x\geq 0\end{cases}}$	$[0,\infty )$	$C^{0}$	Yes	Yes	No
Leaky rectified linear unit (Leaky ReLU)		$f(x)={\begin{cases}0.01x&{\text{for }}x<0\\x&{\text{for }}x\geq 0\end{cases}}$	$f'(x)={\begin{cases}0.01&{\text{for }}x<0\\1&{\text{for }}x\geq 0\end{cases}}$	$(-\infty ,\infty )$	$C^{0}$	Yes	Yes	No
Parameteric rectified linear unit (PReLU)		$f(\alpha ,x)={\begin{cases}\alpha x&{\text{for }}x<0\\x&{\text{for }}x\geq 0\end{cases}}$	$f'(\alpha ,x)={\begin{cases}\alpha &{\text{for }}x<0\\1&{\text{for }}x\geq 0\end{cases}}$	$(-\infty ,\infty )$[2]	$C^{0}$	Yes iff $\alpha \geq 0$	Yes	Yes iff $\alpha =1$
Randomized leaky rectified linear unit (RReLU)		$f(\alpha ,x)={\begin{cases}\alpha x&{\text{for }}x<0\\x&{\text{for }}x\geq 0\end{cases}}$[3]	$f'(\alpha ,x)={\begin{cases}\alpha &{\text{for }}x<0\\1&{\text{for }}x\geq 0\end{cases}}$	$(-\infty ,\infty )$	$C^{0}$	Yes	Yes	No
Exponential linear unit (ELU)		$f(\alpha ,x)={\begin{cases}\alpha (e^{x}-1)&{\text{for }}x<0\\x&{\text{for }}x\geq 0\end{cases}}$	$f'(\alpha ,x)={\begin{cases}f(\alpha ,x)+\alpha &{\text{for }}x<0\\1&{\text{for }}x\geq 0\end{cases}}$	$(-\alpha ,\infty )$	${\begin{cases}C_{1}&{\text{when }}\alpha =1\\C_{0}&{\text{otherwise }}\end{cases}}$	Yes iff $\alpha \geq 0$	Yes iff $0\leq \alpha \leq 1$	Yes iff $\alpha =1$
Scaled exponential linear unit (SELU)		$f(\alpha ,x)=\lambda {\begin{cases}\alpha (e^{x}-1)&{\text{for }}x<0\\x&{\text{for }}x\geq 0\end{cases}}$ with $\lambda =1.0507$ and $\alpha =1.67326$	$f'(\alpha ,x)=\lambda {\begin{cases}\alpha (e^{x})&{\text{for }}x<0\\1&{\text{for }}x\geq 0\end{cases}}$	$(-\lambda \alpha ,\infty )$	$C^{0}$	Yes	No	No
S-shaped rectified linear activation unit (SReLU)		$f_{t_{l},a_{l},t_{r},a_{r}}(x)={\begin{cases}t_{l}+a_{l}(x-t_{l})&{\text{for }}x\leq t_{l}\\x&{\text{for }}t_{l}<x<t_{r}\\t_{r}+a_{r}(x-t_{r})&{\text{for }}x\geq t_{r}\end{cases}}$ $t_{l},a_{l},t_{r},a_{r}$ are parameters.	$f'_{t_{l},a_{l},t_{r},a_{r}}(x)={\begin{cases}a_{l}&{\text{for }}x\leq t_{l}\\1&{\text{for }}t_{l}<x<t_{r}\\a_{r}&{\text{for }}x\geq t_{r}\end{cases}}$	$(-\infty ,\infty )$	$C^{0}$	No	No	No
Inverse square root linear unit (ISRLU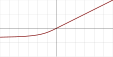)		$f(x)={\begin{cases}{\frac {x}{\sqrt {1+\alpha x^{2}}}}&{\text{for }}x<0\\x&{\text{for }}x\geq 0\end{cases}}$	$f'(x)={\begin{cases}\left({\frac {1}{\sqrt {1+\alpha x^{2}}}}\right)^{3}&{\text{for }}x<0\\1&{\text{for }}x\geq 0\end{cases}}$	$\left(-{\frac {1}{\sqrt {\alpha }}},\infty \right)$	$C^{2}$	Yes	Yes	Yes
Adaptive piecewise linear (APL)		$f(x)=\max(0,x)+\sum _{s=1}^{S}a_{i}^{s}\max(0,-x+b_{i}^{s})$	$f'(x)=H(x)-\sum _{s=1}^{S}a_{i}^{s}H(-x+b_{i}^{s})$[4]	$(-\infty ,\infty )$	$C^{0}$	No	No	No
SoftPlus		$f(x)=\ln(1+e^{x})$	$f'(x)={\frac {1}{1+e^{-x}}}$	$(0,\infty )$	$C^{\infty }$	Yes	Yes	No
Bent identity		$f(x)={\frac {{\sqrt {x^{2}+1}}-1}{2}}+x$	$f'(x)={\frac {x}{2{\sqrt {x^{2}+1}}}}+1$	$(-\infty ,\infty )$	$C^{\infty }$	Yes	Yes	Yes
Sigmoid-weighted linear unit (SiLU) (a.k.a. Swish)		$f(x)=x\cdot \sigma (x)$[5]	$f'(x)=f(x)+\sigma (x)(1-f(x))$[6]	$[\approx -0.28,\infty )$	$C^{\infty }$	No	No	No
SoftExponential		$f(\alpha ,x)={\begin{cases}-{\frac {\ln(1-\alpha (x+\alpha ))}{\alpha }}&{\text{for }}\alpha <0\\x&{\text{for }}\alpha =0\\{\frac {e^{\alpha x}-1}{\alpha }}+\alpha &{\text{for }}\alpha >0\end{cases}}$	$f'(\alpha ,x)={\begin{cases}{\frac {1}{1-\alpha (\alpha +x)}}&{\text{for }}\alpha <0\\e^{\alpha x}&{\text{for }}\alpha \geq 0\end{cases}}$	$(-\infty ,\infty )$	$C^{\infty }$	Yes	Yes	Yes iff $\alpha =0$
Sinusoid		$f(x)=\sin(x)$	$f'(x)=\cos(x)$	$[-1,1]$	$C^{\infty }$	No	No	Yes
Sinc		$f(x)={\begin{cases}1&{\text{for }}x=0\\{\frac {\sin(x)}{x}}&{\text{for }}x\neq 0\end{cases}}$	$f'(x)={\begin{cases}0&{\text{for }}x=0\\{\frac {\cos(x)}{x}}-{\frac {\sin(x)}{x^{2}}}&{\text{for }}x\neq 0\end{cases}}$	$[\approx -.217234,1]$	$C^{\infty }$	No	No	No
Gaussian		$f(x)=e^{-x^{2}}$	$f'(x)=-2xe^{-x^{2}}$	$(0,1]$	$C^{\infty }$	No	No	No

^ Here, H is the Heaviside step function.

^ α is a stochastic variable sampled from a uniform distribution at training time and fixed to the expectation value of the distribution at test time.

^ ^ ^ Here, $\sigma$ is the logistic function.

^ $\alpha >0$ for the range to hold true.

The following table lists activation functions that are not functions of a single fold x from the previous layer or layers:

Name	Equation	Derivatives	Range	Order of continuity
Softmax	$f_{i}({\vec {x}})={\frac {e^{x_{i}}}{\sum _{j=1}^{J}e^{x_{j}}}}$    for i = 1, …, J	${\frac {\partial f_{i}({\vec {x}})}{\partial x_{j}}}=f_{i}({\vec {x}})(\delta _{ij}-f_{j}({\vec {x}}))$[7]	$(0,1)$	$C^{\infty }$
Maxout	$f({\vec {x}})=\max _{i}x_{i}$	${\frac {\partial f}{\partial x_{j}}}={\begin{cases}1&{\text{for }}j={\underset {i}{\operatorname {argmax} }}\,x_{i}\\0&{\text{for }}j\neq {\underset {i}{\operatorname {argmax} }}\,x_{i}\end{cases}}$	$(-\infty ,\infty )$	$C^{0}$

^ Here, $\delta _{ij}$ is the Kronecker delta.

See also

• Logistic function
• Rectifier (neural networks)
• Stability (learning theory)
• Softmax function