1 42 polytope

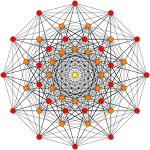421	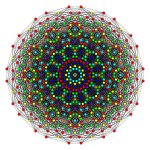142	241
Rectified 421	Rectified 142	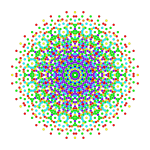Rectified 241
Birectified 421	Trirectified 421
Orthogonal projections in E6 Coxeter plane

In 8-dimensional geometry, the 1₄₂ is a uniform 8-polytope, constructed within the symmetry of the E₈ group.

Its Coxeter symbol is 1₄₂, describing its bifurcating Coxeter-Dynkin diagram, with a single ring on the end of the 1-node sequences.

The rectified 1₄₂ is constructed by points at the mid-edges of the 1₄₂ and is the same as the birectified 2₄₁, and the quadrirectified 4₂₁.

These polytopes are part of a family of 255 (2⁸ − 1) convex uniform polytopes in 8-dimensions, made of uniform polytope facets and vertex figures, defined by all permutations of rings in this Coxeter-Dynkin diagram: .

1₄₂ polytope

142
Type	Uniform 8-polytope
Family	1k2 polytope
Schläfli symbol	{3,34,2}
Coxeter symbol	142
Coxeter diagrams
7-faces	2400: 240 132 2160 141
6-faces	106080: 6720 122 30240 131 69120 {35}
5-faces	725760: 60480 112 181440 121 483840 {34}
4-faces	2298240: 241920 102 604800 111 1451520 {33}
Cells	3628800: 1209600 101 2419200 {32}
Faces	2419200 {3}
Edges	483840
Vertices	17280
Vertex figure	t2{36}
Petrie polygon	30-gon
Coxeter group	E8, [34,2,1]
Properties	convex

The 1₄₂ is composed of 2400 facets: 240 1₃₂ polytopes, and 2160 7-demicubes (1₄₁). Its vertex figure is a birectified 7-simplex.

This polytope, along with the demiocteract, can tessellate 8-dimensional space, represented by the symbol 1₅₂, and Coxeter-Dynkin diagram: .

Alternate names

• E. L. Elte (1912) excluded this polytope from his listing of semiregular polytopes, because it has more than two types of 6-faces, but under his naming scheme it would be called V₁₇₂₈₀ for its 17280 vertices.
• Coxeter named it 1₄₂ for its bifurcating Coxeter-Dynkin diagram, with a single ring on the end of the 1-node branch.
• Diacositetracont-dischiliahectohexaconta-zetton (Acronym bif) - 240-2160 facetted polyzetton (Jonathan Bowers)

The 17280 vertices can be defined as sign and location permutations of:

All sign combinations (32): (280×32=8960 vertices)

(4, 2, 2, 2, 2, 0, 0, 0)

Half of the sign combinations (128): ((1+8+56)×128=8320 vertices)

(2, 2, 2, 2, 2, 2, 2, 2)

(5, 1, 1, 1, 1, 1, 1, 1)

(3, 3, 3, 1, 1, 1, 1, 1)

The edge length is 2√2 in this coordinate set, and the polytope radius is 4√2.

Construction

It is created by a Wythoff construction upon a set of 8 hyperplane mirrors in 8-dimensional space.

The facet information can be extracted from its Coxeter-Dynkin diagram: .

Removing the node on the end of the 2-length branch leaves the 7-demicube, 1₄₁, .

Removing the node on the end of the 4-length branch leaves the 1₃₂, .

The vertex figure is determined by removing the ringed node and ringing the neighboring node. This makes the birectified 7-simplex, 0₄₂, .

Projections

Orthographic projections are shown for the sub-symmetries of E₈: E₇, E₆, B₈, B₇, B₆, B₅, B₄, B₃, B₂, A₇, and A₅ Coxeter planes, as well as two more symmetry planes of order 20 and 24. Vertices are shown as circles, colored by their order of overlap in each projective plane.

E8 [30]	E7 [18]	E6 [12]
(1)	(1,3,6)	(8,16,24,32,48,64,96)
[20]	[24]	[6]
		(1,2,3,4,5,6,7,8,10,11,12,14,16,18,19,20)

D3 / B2 / A3 [4]	D4 / B3 / A2 [6]	D5 / B4 [8]
(32,160,192,240,480,512,832,960)	(72,216,432,720,864,1080)	(8,16,24,32,48,64,96)
D6 / B5 / A4 [10]	D7 / B6 [12]	D8 / B7 / A6 [14]
B8 [16/2]	A5 [6]	A7 [8]

Related polytopes and honeycombs

1k2 figures in n dimensions
Space	Finite						Euclidean	Hyperbolic
n	3	4	5	6	7	8	9	10
Coxeter group	E3=A2A1	E4=A4	E5=D5	E6	E7	E8	E9 = ${\tilde {E}}_{8}$ = E8+	E10 = ${\bar {T}}_{8}$ = E8++
Coxeter diagram
Symmetry (order)	[3−1,2,1]	[30,2,1]	[31,2,1]	[[32,2,1]]	[33,2,1]	[34,2,1]	[35,2,1]	[36,2,1]
Order	12	120	1,920	103,680	2,903,040	696,729,600	∞
Graph							-	-
Name	1−1,2	102	112	122	132	142	152	162

Rectified 1₄₂ polytope

Rectified 142
Type	Uniform 8-polytope
Schläfli symbol	t1{3,34,2}
Coxeter symbol	0421
Coxeter diagrams
7-faces	19680
6-faces	382560
5-faces	2661120
4-faces	9072000
Cells	16934400
Faces	16934400
Edges	7257600
Vertices	483840
Vertex figure	{3,3,3}×{3}×{}
Coxeter group	E8, [34,2,1]
Properties	convex

The rectified 1₄₂ is named from being a rectification of the 1₄₂ polytope, with vertices positioned at the mid-edges of the 1₄₂.

Alternate names

• Birectified 2₄₁ polytope
• Quadrirectified 4₂₁ polytope
• Rectified diacositetracont-dischiliahectohexaconta-zetton as a rectified 240-2160 facetted polyzetton (Acronym buffy) (Jonathan Bowers)

Construction

It is created by a Wythoff construction upon a set of 8 hyperplane mirrors in 8-dimensional space.

The facet information can be extracted from its Coxeter-Dynkin diagram: .

Removing the node on the end of the 1-length branch leaves the birectified 7-simplex,

Removing the node on the end of the 2-length branch leaves the 7-demicube, 1₄₁, .

Removing the node on the end of the 3-length branch leaves the 1₃₂, .

The vertex figure is determined by removing the ringed node and ringing the neighboring node. This makes the 5-cell-triangle duoprism prism, .

Projections

Orthographic projections are shown for the sub-symmetries of B₆, B₅, B₄, B₃, B₂, A₇, and A₅ Coxeter planes. Vertices are shown as circles, colored by their order of overlap in each projective plane.

(Planes for E₈: E₇, E₆, B₈, B₇, [20], [24] are not shown for being too large to display.)

D3 / B2 / A3 [4]	D4 / B3 / A2 [6]	D5 / B4 [8]
D6 / B5 / A4 [10]	D7 / B6 [12]	[6]
A5 [6]	A7 [8]

See also

• List of E8 polytopes

References

• H. S. M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
• Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• Klitzing, Richard. "8D Uniform polyzetta". o3o3o3x *c3o3o3o3o - bif, o3o3o3x *c3o3o3o3o - buffy