Order-7 tetrahedral honeycomb
| Order-7 tetrahedral honeycomb | |
|---|---|
| Type | Hyperbolic regular honeycomb |
| Schläfli symbols | {3,3,7} |
| Coxeter diagrams |    
|
| Cells | {3,3} 
|
| Faces | {3} |
| Edge figure | {7} |
| Vertex figure | {3,7} 
|
| Dual | {7,3,3} |
| Coxeter group | [7,3,3] |
| Properties | Regular |
In the geometry of hyperbolic 3-space, the order-7 tetrahedral honeycomb is a regular space-filling tessellation (or honeycomb) with Schläfli symbol {3,3,7}. It has seven tetrahedra {3,3} around each edge. All vertices are ultra-ideal (existing beyond the ideal boundary) with infinitely many tetrahedra existing around each vertex in an order-7 triangular tiling vertex arrangement.
Images
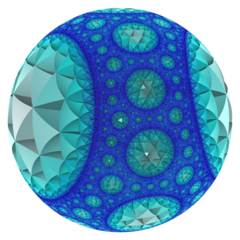 Poincaré disk model (cell-centered) |
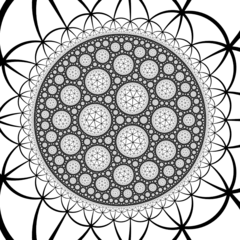 Rendered intersection of honeycomb with the ideal plane in Poincaré half-space model |
Related polytopes and honeycombs
It is a part of a sequence of regular polychora and honeycombs with tetrahedral cells, {3,3,p}.
| {3,3,p} polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Space | S3 | H3 | |||||||||
| Form | Finite | Paracompact | Noncompact | ||||||||
| Name | {3,3,3}
|
{3,3,4}  
|
{3,3,5}
|
{3,3,6} 
|
{3,3,7}
|
{3,3,8} 
|
... {3,3,∞} 
| ||||
| Image | 
|
|
|
|
|
|
| ||||
| Vertex figure |
 {3,3}
|
 {3,4}
|
 {3,5}
|
 {3,6}
|
{3,7}
|
 {3,8}
|
 {3,∞}
| ||||
It is a part of a sequence of hyperbolic honeycombs with order-7 triangular tiling vertex figures, {p,3,7}.
| {3,3,7} | {4,3,7} | {5,3,7} | {6,3,7} | {7,3,7} | {8,3,7} | {∞,3,7} |
|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
It is a part of a sequence of hyperbolic honeycombs, {3,p,7}.
Order-8 tetrahedral honeycomb
| Order-8 tetrahedral honeycomb | |
|---|---|
| Type | Hyperbolic regular honeycomb |
| Schläfli symbols | {3,3,8} {3,(3,4,3)} |
| Coxeter diagrams |  =
|
| Cells | {3,3}
|
| Faces | {3} |
| Edge figure | {8} |
| Vertex figure | {3,8} {(3,4,3)} 
|
| Dual | {8,3,3} |
| Coxeter group | [3,3,8] [3,((3,4,3))] |
| Properties | Regular |
In the geometry of hyperbolic 3-space, the order-8 tetrahedral honeycomb is a regular space-filling tessellation (or honeycomb) with Schläfli symbol {3,3,8}. It has eight tetrahedra {3,3} around each edge. All vertices are ultra-ideal (existing beyond the ideal boundary) with infinitely many tetrahedra existing around each vertex in an order-8 triangular tiling vertex arrangement.
Poincaré disk model (cell-centered) |
 Rendered intersection of honeycomb with the ideal plane in Poincaré half-space model |
It has a second construction as a uniform honeycomb, Schläfli symbol {3,(3,4,3)}, Coxeter diagram, , with alternating types or colors of tetrahedral cells. In Coxeter notation the half symmetry is [3,3,8,1+] = [3,((3,4,3))].
Infinite-order tetrahedral honeycomb
| Infinite-order tetrahedral honeycomb | |
|---|---|
| Type | Hyperbolic regular honeycomb |
| Schläfli symbols | {3,3,∞} {3,(3,∞,3)} |
| Coxeter diagrams | =
|
| Cells | {3,3}
|
| Faces | {3} |
| Edge figure | {∞} |
| Vertex figure | {3,∞} {(3,∞,3)} 
|
| Dual | {∞,3,3} |
| Coxeter group | [∞,3,3] [3,((3,∞,3))] |
| Properties | Regular |
In the geometry of hyperbolic 3-space, the infinite-order tetrahedral honeycomb is a regular space-filling tessellation (or honeycomb) with Schläfli symbol {3,3,∞}. It has infinitely many tetrahedra {3,3} around each edge. All vertices are ultra-ideal (existing beyond the ideal boundary) with infinitely many tetrahedra existing around each vertex in an infinite-order triangular tiling vertex arrangement.
Poincaré disk model (cell-centered) |
 Rendered intersection of honeycomb with the ideal plane in Poincaré half-space model |
It has a second construction as a uniform honeycomb, Schläfli symbol {3,(3,∞,3)}, Coxeter diagram, = , with alternating types or colors of tetrahedral cells. In Coxeter notation the half symmetry is [3,3,∞,1+] = [3,((3,∞,3))].
See also
References
- Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8. (Tables I and II: Regular polytopes and honeycombs, pp. 294–296)
- The Beauty of Geometry: Twelve Essays (1999), Dover Publications, LCCN 99-35678, ISBN 0-486-40919-8 (Chapter 10, Regular Honeycombs in Hyperbolic Space) Table III
- Jeffrey R. Weeks The Shape of Space, 2nd edition ISBN 0-8247-0709-5 (Chapters 16–17: Geometries on Three-manifolds I,II)
- George Maxwell, Sphere Packings and Hyperbolic Reflection Groups, JOURNAL OF ALGEBRA 79,78-97 (1982) [1]
- Hao Chen, Jean-Philippe Labbé, Lorentzian Coxeter groups and Boyd-Maxwell ball packings, (2013)[2]
- Visualizing Hyperbolic Honeycombs arXiv:1511.02851 Roice Nelson, Henry Segerman (2015)
External links
- John Baez, Visual insights: {7,3,3} Honeycomb (2014/08/01) {7,3,3} Honeycomb Meets Plane at Infinity (2014/08/14)
- Danny Calegari, Kleinian, a tool for visualizing Kleinian groups, Geometry and the Imagination 4 March 2014. [3]