Heptagon
| Regular heptagon | |
|---|---|
 A regular heptagon | |
| Type | Regular polygon |
| Edges and vertices | 7 |
| Schläfli symbol | {7} |
| Coxeter–Dynkin diagrams | |
| Symmetry group | Dihedral (D7), order 2×7 |
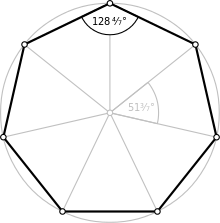
| Internal angle (degrees) | ≈128.571° |
| Properties | Convex, cyclic, equilateral, isogonal, isotoxal |
| Dual polygon | Self |
In geometry, a heptagon or septagon is a seven-sided polygon or 7-gon.
The heptagon is sometimes referred to as the septagon, using "sept-" (an elision of septua-, a Latin-derived numerical prefix, rather than hepta-, a Greek-derived numerical prefix; both are cognate) together with the Greek suffix "-agon" meaning angle.
Regular heptagon
[edit]A regular heptagon, in which all sides and all angles are equal, has internal angles of 5π/7 radians (1284⁄7 degrees). Its Schläfli symbol is {7}.
Area
[edit]The area (A) of a regular heptagon of side length a is given by:
This can be seen by subdividing the unit-sided heptagon into seven triangular "pie slices" with vertices at the center and at the heptagon's vertices, and then halving each triangle using the apothem as the common side. The apothem is half the cotangent of and the area of each of the 14 small triangles is one-fourth of the apothem.
The area of a regular heptagon inscribed in a circle of radius R is while the area of the circle itself is thus the regular heptagon fills approximately 0.8710 of its circumscribed circle.
Construction
[edit]As 7 is a Pierpont prime but not a Fermat prime, the regular heptagon is not constructible with compass and straightedge but is constructible with a marked ruler and compass. It is the smallest regular polygon with this property. This type of construction is called a neusis construction. It is also constructible with compass, straightedge and angle trisector. The impossibility of straightedge and compass construction follows from the observation that is a zero of the irreducible cubic x3 + x2 − 2x − 1. Consequently, this polynomial is the minimal polynomial of 2cos(2π⁄7), whereas the degree of the minimal polynomial for a constructible number must be a power of 2.
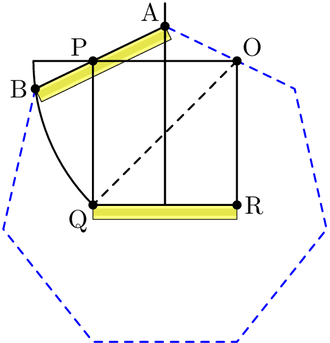 A neusis construction of the interior angle in a regular heptagon. |
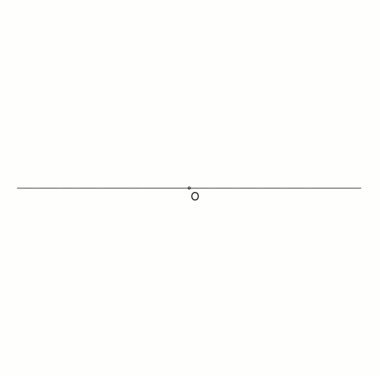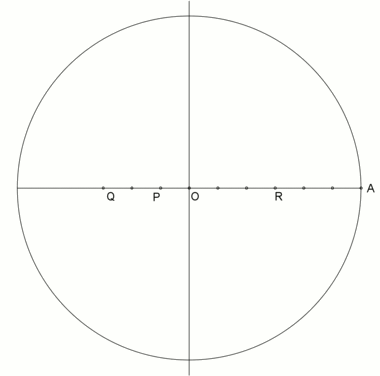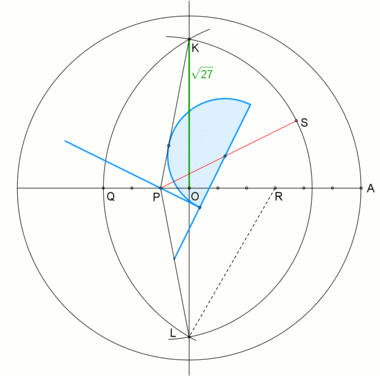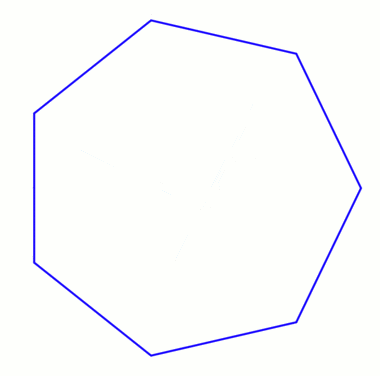 An animation from a neusis construction with radius of circumcircle , according to Andrew M. Gleason[1] based on the angle trisection by means of the tomahawk. This construction relies on the fact that
|

An animation from a neusis construction with marked ruler, according to David Johnson Leisk (Crockett Johnson).
Approximation
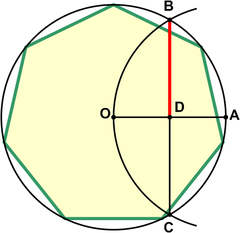
[edit]An approximation for practical use with an error of about 0.2% is to use half the side of an equilateral triangle inscribed in the same circle as the length of the side of a regular heptagon. It is unknown who first found this approximation, but it was mentioned by Heron of Alexandria's Metrica in the 1st century AD, was well known to medieval Islamic mathematicians, and can be found in the work of Albrecht Dürer.[2][3] Let A lie on the circumference of the circumcircle. Draw arc BOC. Then gives an approximation for the edge of the heptagon.
This approximation uses for the side of the heptagon inscribed in the unit circle while the exact value is .
Example to illustrate the error:
At a circumscribed circle radius r = 1 m, the absolute error of the 1st side would be approximately -1.7 mm
Other approximations
[edit]There are other approximations of a heptagon using compass and straightedge, but they are time consuming to draw. [4]
Symmetry
[edit]
The regular heptagon belongs to the D7h point group (Schoenflies notation), order 28. The symmetry elements are: a 7-fold proper rotation axis C7, a 7-fold improper rotation axis, S7, 7 vertical mirror planes, σv, 7 2-fold rotation axes, C2, in the plane of the heptagon and a horizontal mirror plane, σh, also in the heptagon's plane.[6]
Diagonals and heptagonal triangle
[edit]
The regular heptagon's side a, shorter diagonal b, and longer diagonal c, with a<b<c, satisfy[7]: Lemma 1
- (the optic equation)
and hence
and[7]: Coro. 2
Thus –b/c, c/a, and a/b all satisfy the cubic equation However, no algebraic expressions with purely real terms exist for the solutions of this equation, because it is an example of casus irreducibilis.
The approximate lengths of the diagonals in terms of the side of the regular heptagon are given by
We also have[8]
and
A heptagonal triangle has vertices coinciding with the first, second, and fourth vertices of a regular heptagon (from an arbitrary starting vertex) and angles and Thus its sides coincide with one side and two particular diagonals of the regular heptagon.[7]
In polyhedra
[edit]Apart from the heptagonal prism and heptagonal antiprism, no convex polyhedron made entirely out of regular polygons contains a heptagon as a face.
Star heptagons
[edit]Two kinds of star heptagons (heptagrams) can be constructed from regular heptagons, labeled by Schläfli symbols {7/2}, and {7/3}, with the divisor being the interval of connection.
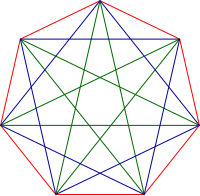
Blue, {7/2} and green {7/3} star heptagons inside a red heptagon.
Tiling and packing
[edit]A regular triangle, heptagon, and 42-gon can completely fill a plane vertex. However, there is no tiling of the plane with only these polygons, because there is no way to fit one of them onto the third side of the triangle without leaving a gap or creating an overlap. In the hyperbolic plane, tilings by regular heptagons are possible. There are also concave heptagon tilings possible in the Euclidean plane.[9]

The regular heptagon has a double lattice packing of the Euclidean plane of packing density approximately 0.89269. This has been conjectured to be the lowest density possible for the optimal double lattice packing density of any convex set, and more generally for the optimal packing density of any convex set.[10]
Empirical examples
[edit]The United Kingdom, since 1982, has two heptagonal coins, the 50p and 20p pieces. The Barbados Dollar are also heptagonal. Strictly, the shape of the coins is a Reuleaux heptagon, a curvilinear heptagon which has curves of constant width; the sides are curved outwards to allow the coins to roll smoothly when they are inserted into a vending machine. Botswana pula coins in the denominations of 2 Pula, 1 Pula, 50 Thebe and 5 Thebe are also shaped as equilateral-curve heptagons. Coins in the shape of Reuleaux heptagons are also in circulation in Mauritius, U.A.E., Tanzania, Samoa, Papua New Guinea, São Tomé and Príncipe, Haiti, Jamaica, Liberia, Ghana, the Gambia, Jordan, Jersey, Guernsey, Isle of Man, Gibraltar, Guyana, Solomon Islands, Falkland Islands and Saint Helena. The 1000 Kwacha coin of Zambia is a true heptagon.
The Brazilian 25-cent coin has a heptagon inscribed in the coin's disk. Some old versions of the coat of arms of Georgia, including in Soviet days, used a {7/2} heptagram as an element.
A number of coins, including the 20 euro cent coin, have heptagonal symmetry in a shape called the Spanish flower.
In architecture, heptagonal floor plans are very rare. A remarkable example is the Mausoleum of Prince Ernst in Stadthagen, Germany.
Many police badges in the US have a {7/2} heptagram outline.
See also
[edit]References
[edit]- ^ Gleason, Andrew Mattei (March 1988). "Angle trisection, the heptagon, and the triskaidecagon p. 186 (Fig.1) –187" (PDF). The American Mathematical Monthly. 95 (3): 185–194. doi:10.2307/2323624. JSTOR 2323624. Archived from the original (PDF) on 19 December 2015.
- ^ Hogendijk, Jan P. (1987). "Abu'l-Jūd's Answer to a Question of al-Bīrūnī Concerning the Regular Heptagon" (PDF). Annals of the New York Academy of Sciences. 500 (1): 175–183. doi:10.1111/j.1749-6632.1987.tb37202.x.
- ^ G.H. Hughes, "The Polygons of Albrecht Dürer-1525, The Regular Heptagon", Fig. 11 the side of the Heptagon (7) Fig. 15, image on the left side, retrieved on 4 December 2015
- ^ raumannkidwai. "Heptagon." Chart. Geogebra. Accessed January 20, 2024. https://www.geogebra.org/classic/CvsudDWr.
- ^ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)
- ^ Salthouse, J.A; Ware, M.J. (1972). Point group character tables and related data. Cambridge: Cambridge University Press. ISBN 0-521-08139-4.
- ^ a b c Abdilkadir Altintas, "Some Collinearities in the Heptagonal Triangle", Forum Geometricorum 16, 2016, 249–256.http://forumgeom.fau.edu/FG2016volume16/FG201630.pdf
- ^ Leon Bankoff and Jack Garfunkel, "The heptagonal triangle", Mathematics Magazine 46 (1), January 1973, 7–19.
- ^ Sycamore916, ed. "Heptagon." Polytope Wiki. Last modified November 2023. Accessed January 20, 2024. https://polytope.miraheze.org/wiki/Heptagon.
- ^ Kallus, Yoav (2015). "Pessimal packing shapes". Geometry & Topology. 19 (1): 343–363. arXiv:1305.0289. doi:10.2140/gt.2015.19.343. MR 3318753.
External links
[edit]- Definition and properties of a heptagon With interactive animation
- Heptagon according Johnson
- Another approximate construction method
- Polygons – Heptagons
- Recently discovered and highly accurate approximation for the construction of a regular heptagon.
- Heptagon, an approximating construction as an animation
- A heptagon with a given side, an approximating construction as an animation
Heptagon