Biggs–Smith graph
| Biggs–Smith graph | |
|---|---|
 The Biggs–Smith graph | |
| Vertices | 102 |
| Edges | 153 |
| Radius | 7 |
| Diameter | 7 |
| Girth | 9 |
| Automorphisms | 2448 (PSL(2,17)) |
| Chromatic number | 3 |
| Chromatic index | 3 |
| Properties | Symmetric Distance-regular Cubic Hamiltonian |
| Table of graphs and parameters | |
In the mathematical field of graph theory, the Biggs–Smith graph is a 3-regular graph with 102 vertices and 153 edges.[1]
It has chromatic number 3, chromatic index 3, radius 7, diameter 7 and girth 9. It is also a 3-vertex-connected graph and a 3-edge-connected graph.
All the cubic distance-regular graphs are known.[2] The Biggs–Smith graph is one of the 13 such graphs.
Algebraic properties
[edit]The automorphism group of the Biggs–Smith graph is a group of order 2448[3] isomorphic to the projective special linear group PSL(2,17). It acts transitively on the vertices, on the edges and on the arcs of the graph. Therefore, the Biggs–Smith graph is a symmetric graph. It has automorphisms that take any vertex to any other vertex and any edge to any other edge. According to the Foster census, the Biggs–Smith graph, referenced as F102A, is the only cubic symmetric graph on 102 vertices.[4]
The Biggs–Smith graph is also uniquely determined by its graph spectrum, the set of graph eigenvalues of its adjacency matrix.[5]
The characteristic polynomial of the Biggs–Smith graph is : .
Gallery
[edit]-
The chromatic number of the Biggs–Smith graph is 3.
-
The chromatic index of the Biggs–Smith graph is 3.
-
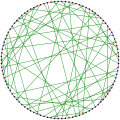
Alternative drawing of the Biggs–Smith graph
-
Another drawing of the Biggs–Smith graph
-
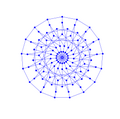
Decomposition of the Biggs–Smith graph into 6 sets of size 17
-
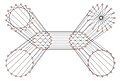
Another rendering of the Biggs–Smith graph, once again showing that it is an order-17 graph expansion of the H graph
References
[edit]- ^ Weisstein, Eric W. "Biggs–Smith Graph". MathWorld.
- ^ Brouwer, A. E.; Cohen, A. M.; and Neumaier, A. Distance-Regular Graphs. New York: Springer-Verlag, 1989.
- ^ "G-17 Biggs-Smith graph", Encyclopedia of graphs, retrieved 2024-02-22
- ^ Conder, M. and Dobcsányi, P. "Trivalent Symmetric Graphs Up to 768 Vertices." J. Combin. Math. Combin. Comput. 40, 41–63, 2002.
- ^ E. R. van Dam and W. H. Haemers, Spectral Characterizations of Some Distance-Regular Graphs. J. Algebraic Combin. 15, pages 189–202, 2003
- On trivalent graphs, NL Biggs, DH Smith - Bulletin of the London Mathematical Society, 3 (1971) 155–158.