Chomsky normal form
In formal language theory, a context-free grammar, G, is said to be in Chomsky normal form (first described by Noam Chomsky)[1] if all of its production rules are of the form:[2][3]
- A → BC, or
- A → a, or
- S → ε,
where A, B, and C are nonterminal symbols, the letter a is a terminal symbol (a symbol that represents a constant value), S is the start symbol, and ε denotes the empty string. Also, neither B nor C may be the start symbol, and the third production rule can only appear if ε is in L(G), the language produced by the context-free grammar G.[4]: 92–93, 106
Every grammar in Chomsky normal form is context-free, and conversely, every context-free grammar can be transformed into an equivalent one[note 1] which is in Chomsky normal form and has a size no larger than the square of the original grammar's size.
Converting a grammar to Chomsky normal form
[edit]To convert a grammar to Chomsky normal form, a sequence of simple transformations is applied in a certain order; this is described in most textbooks on automata theory.[4]: 87–94 [5][6][7] The presentation here follows Hopcroft, Ullman (1979), but is adapted to use the transformation names from Lange, Leiß (2009).[8][note 2] Each of the following transformations establishes one of the properties required for Chomsky normal form.
START: Eliminate the start symbol from right-hand sides
[edit]Introduce a new start symbol S0, and a new rule
- S0 → S,
where S is the previous start symbol. This does not change the grammar's produced language, and S0 will not occur on any rule's right-hand side.
TERM: Eliminate rules with nonsolitary terminals
[edit]To eliminate each rule
- A → X1 ... a ... Xn
with a terminal symbol a being not the only symbol on the right-hand side, introduce, for every such terminal, a new nonterminal symbol Na, and a new rule
- Na → a.
Change every rule
- A → X1 ... a ... Xn
to
- A → X1 ... Na ... Xn.
If several terminal symbols occur on the right-hand side, simultaneously replace each of them by its associated nonterminal symbol. This does not change the grammar's produced language.[4]: 92
BIN: Eliminate right-hand sides with more than 2 nonterminals
[edit]Replace each rule
- A → X1 X2 ... Xn
with more than 2 nonterminals X1,...,Xn by rules
- A → X1 A1,
- A1 → X2 A2,
- ... ,
- An-2 → Xn-1 Xn,
where Ai are new nonterminal symbols. Again, this does not change the grammar's produced language.[4]: 93
DEL: Eliminate ε-rules
[edit]An ε-rule is a rule of the form
- A → ε,
where A is not S0, the grammar's start symbol.
To eliminate all rules of this form, first determine the set of all nonterminals that derive ε. Hopcroft and Ullman (1979) call such nonterminals nullable, and compute them as follows:
- If a rule A → ε exists, then A is nullable.
- If a rule A → X1 ... Xn exists, and every single Xi is nullable, then A is nullable, too.
Obtain an intermediate grammar by replacing each rule
- A → X1 ... Xn
by all versions with some nullable Xi omitted. By deleting in this grammar each ε-rule, unless its left-hand side is the start symbol, the transformed grammar is obtained.[4]: 90
For example, in the following grammar, with start symbol S0,
- S0 → AbB | C
- B → AA | AC
- C → b | c
- A → a | ε
the nonterminal A, and hence also B, is nullable, while neither C nor S0 is. Hence the following intermediate grammar is obtained:[note 3]
- S0 → AbB | Ab
B|AbB |AbB| C - B → AA |
AA | AA|AεA| AC |AC - C → b | c
- A → a | ε
In this grammar, all ε-rules have been "inlined at the call site".[note 4] In the next step, they can hence be deleted, yielding the grammar:
- S0 → AbB | Ab | bB | b | C
- B → AA | A | AC | C
- C → b | c
- A → a
This grammar produces the same language as the original example grammar, viz. {ab,aba,abaa,abab,abac,abb,abc,b,ba,baa,bab,bac,bb,bc,c}, but has no ε-rules.
UNIT: Eliminate unit rules
[edit]A unit rule is a rule of the form
- A → B,
where A, B are nonterminal symbols. To remove it, for each rule
- B → X1 ... Xn,
where X1 ... Xn is a string of nonterminals and terminals, add rule
- A → X1 ... Xn
unless this is a unit rule which has already been (or is being) removed. The skipping of nonterminal symbol B in the resulting grammar is possible due to B being a member of the unit closure of nonterminal symbol A.[9]
Order of transformations
[edit]| Transformation X always preserves ( resp. may destroy ( | |||||
Y X
|
START | TERM | BIN | DEL | UNIT |
|---|---|---|---|---|---|
| START | |||||
| TERM | |||||
| BIN | |||||
| DEL | |||||
| UNIT | ( |
||||
| *UNIT preserves the result of DEL if START had been called before. | |||||
When choosing the order in which the above transformations are to be applied, it has to be considered that some transformations may destroy the result achieved by other ones. For example, START will re-introduce a unit rule if it is applied after UNIT. The table shows which orderings are admitted.
Moreover, the worst-case bloat in grammar size[note 5] depends on the transformation order. Using |G| to denote the size of the original grammar G, the size blow-up in the worst case may range from |G|2 to 22 |G|, depending on the transformation algorithm used.[8]: 7 The blow-up in grammar size depends on the order between DEL and BIN. It may be exponential when DEL is done first, but is linear otherwise. UNIT can incur a quadratic blow-up in the size of the grammar.[8]: 5 The orderings START,TERM,BIN,DEL,UNIT and START,BIN,DEL,UNIT,TERM lead to the least (i.e. quadratic) blow-up.
Example
[edit]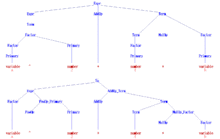
The following grammar, with start symbol Expr, describes a simplified version of the set of all syntactical valid arithmetic expressions in programming languages like C or Algol60. Both number and variable are considered terminal symbols here for simplicity, since in a compiler front end their internal structure is usually not considered by the parser. The terminal symbol "^" denoted exponentiation in Algol60.
Expr → Term | Expr AddOp Term | AddOp Term Term → Factor | Term MulOp Factor Factor → Primary | Factor ^ Primary Primary → number | variable | ( Expr ) AddOp → + | − MulOp → * | /
In step "START" of the above conversion algorithm, just a rule S0→Expr is added to the grammar. After step "TERM", the grammar looks like this:
S0 → Expr Expr → Term | Expr AddOp Term | AddOp Term Term → Factor | Term MulOp Factor Factor → Primary | Factor PowOp Primary Primary → number | variable | Open Expr Close AddOp → + | − MulOp → * | / PowOp → ^ Open → ( Close → )
After step "BIN", the following grammar is obtained:
S0 → Expr Expr → Term | Expr AddOp_Term | AddOp Term Term → Factor | Term MulOp_Factor Factor → Primary | Factor PowOp_Primary Primary → number | variable | Open Expr_Close AddOp → + | − MulOp → * | / PowOp → ^ Open → ( Close → ) AddOp_Term → AddOp Term MulOp_Factor → MulOp Factor PowOp_Primary → PowOp Primary Expr_Close → Expr Close
Since there are no ε-rules, step "DEL" does not change the grammar. After step "UNIT", the following grammar is obtained, which is in Chomsky normal form:
S0 → number | variable | Open Expr_Close | Factor PowOp_Primary | Term MulOp_Factor | Expr AddOp_Term | AddOp Term Expr → number | variable | Open Expr_Close | Factor PowOp_Primary | Term MulOp_Factor | Expr AddOp_Term | AddOp Term Term → number | variable | Open Expr_Close | Factor PowOp_Primary | Term MulOp_Factor Factor → number | variable | Open Expr_Close | Factor PowOp_Primary Primary → number | variable | Open Expr_Close AddOp → + | − MulOp → * | / PowOp → ^ Open → ( Close → ) AddOp_Term → AddOp Term MulOp_Factor → MulOp Factor PowOp_Primary → PowOp Primary Expr_Close → Expr Close
The Na introduced in step "TERM" are PowOp, Open, and Close. The Ai introduced in step "BIN" are AddOp_Term, MulOp_Factor, PowOp_Primary, and Expr_Close.
Alternative definition
[edit]Chomsky reduced form
[edit]Another way[4]: 92 [10] to define the Chomsky normal form is:
A formal grammar is in Chomsky reduced form if all of its production rules are of the form:
- or
- ,
where , and are nonterminal symbols, and is a terminal symbol. When using this definition, or may be the start symbol. Only those context-free grammars which do not generate the empty string can be transformed into Chomsky reduced form.
Floyd normal form
[edit]In a letter where he proposed a term Backus–Naur form (BNF), Donald E. Knuth implied a BNF "syntax in which all definitions have such a form may be said to be in 'Floyd Normal Form'",
- or
- or
- ,
where , and are nonterminal symbols, and is a terminal symbol, because Robert W. Floyd found any BNF syntax can be converted to the above one in 1961.[11] But he withdrew this term, "since doubtless many people have independently used this simple fact in their own work, and the point is only incidental to the main considerations of Floyd's note."[12] While Floyd's note cites Chomsky's original 1959 article, Knuth's letter does not.
Application
[edit]Besides its theoretical significance, CNF conversion is used in some algorithms as a preprocessing step, e.g., the CYK algorithm, a bottom-up parsing for context-free grammars, and its variant probabilistic CKY.[13]
See also
[edit]- Backus–Naur form
- CYK algorithm
- Greibach normal form
- Kuroda normal form
- Pumping lemma for context-free languages — its proof relies on the Chomsky normal form
Notes
[edit]- ^ that is, one that produces the same language
- ^ For example, Hopcroft, Ullman (1979) merged TERM and BIN into a single transformation.
- ^ indicating a kept and omitted nonterminal N by N and
N, respectively - ^ If the grammar had a rule S0 → ε, it could not be "inlined", since it had no "call sites". Therefore it could not be deleted in the next step.
- ^ i.e. written length, measured in symbols
References
[edit]- ^ Chomsky, Noam (1959). "On Certain Formal Properties of Grammars". Information and Control. 2 (2): 137–167. doi:10.1016/S0019-9958(59)90362-6. Here: Sect.6, p.152ff.
- ^ D'Antoni, Loris. "Page 7, Lecture 9: Bottom-up Parsing Algorithms" (PDF). CS536-S21 Intro to Programming Languages and Compilers. University of Wisconsin-Madison. Archived (PDF) from the original on 2021-07-19.
- ^ Sipser, Michael (2006). Introduction to the theory of computation (2nd ed.). Boston: Thomson Course Technology. Definition 2.8. ISBN 0-534-95097-3. OCLC 58544333.
- ^ a b c d e f Hopcroft, John E.; Ullman, Jeffrey D. (1979). Introduction to Automata Theory, Languages and Computation. Reading, Massachusetts: Addison-Wesley Publishing. ISBN 978-0-201-02988-8.
- ^ Hopcroft, John E.; Motwani, Rajeev; Ullman, Jeffrey D. (2006). Introduction to Automata Theory, Languages, and Computation (3rd ed.). Addison-Wesley. ISBN 978-0-321-45536-9. Section 7.1.5, p.272
- ^ Rich, Elaine (2007). "11.8 Normal Forms". Automata, Computability, and Complexity: Theory and Applications (PDF) (1st ed.). Prentice-Hall. p. 169. ISBN 978-0132288064. Archived from the original (PDF) on 2023-01-17.
- ^ Wegener, Ingo (1993). Theoretische Informatik - Eine algorithmenorientierte Einführung. Leitfäden und Mongraphien der Informatik (in German). Stuttgart: B. G. Teubner. ISBN 978-3-519-02123-0. Section 6.2 "Die Chomsky-Normalform für kontextfreie Grammatiken", p. 149–152
- ^ a b c Lange, Martin; Leiß, Hans (2009). "To CNF or not to CNF? An Efficient Yet Presentable Version of the CYK Algorithm" (PDF). Informatica Didactica. 8. Archived (PDF) from the original on 2011-07-19.
- ^ Allison, Charles D. (2022). Foundations of Computing: An Accessible Introduction to Automata and Formal Languages. Fresh Sources, Inc. p. 176. ISBN 9780578944173.
- ^ Hopcroft et al. (2006)[page needed]
- ^ Floyd, Robert W. (1961). "Note on mathematical induction in phrase structure grammars" (PDF). Information and Control. 4 (4): 353–358. doi:10.1016/S0019-9958(61)80052-1. Archived (PDF) from the original on 2021-03-05. Here: p.354
- ^ Knuth, Donald E. (December 1964). "Backus Normal Form vs. Backus Naur Form". Communications of the ACM. 7 (12): 735–736. doi:10.1145/355588.365140. S2CID 47537431.
- ^ Jurafsky, Daniel; Martin, James H. (2008). Speech and Language Processing (2nd ed.). Pearson Prentice Hall. p. 465. ISBN 978-0-13-187321-6.
Further reading
[edit]- Cole, Richard. Converting CFGs to CNF (Chomsky Normal Form), October 17, 2007. (pdf) — uses the order TERM, BIN, START, DEL, UNIT.
- John Martin (2003). Introduction to Languages and the Theory of Computation. McGraw Hill. ISBN 978-0-07-232200-2. (Pages 237–240 of section 6.6: simplified forms and normal forms.)
- Michael Sipser (1997). Introduction to the Theory of Computation. PWS Publishing. ISBN 978-0-534-94728-6. (Pages 98–101 of section 2.1: context-free grammars. Page 156.)
- Charles D. Allison (2021) (20 August 2021). Foundations of Computing: An Accessible Introduction to Formal Language. Fresh Sources, Inc. ISBN 9780578944173.
{{cite book}}: CS1 maint: numeric names: authors list (link) (pages 171-183 of section 7.1: Chomsky Normal Form) - Sipser, Michael. Introduction to the Theory of Computation, 2nd edition.
- Alexander Meduna (6 December 2012). Automata and Languages: Theory and Applications. Springer Science & Business Media. ISBN 978-1-4471-0501-5.












