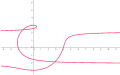
Conchoid of Dürer

In geometry, the conchoid of Dürer, also called Dürer's shell curve, is a plane, algebraic curve, named after Albrecht Dürer and introduced in 1525. It is not a true conchoid.
Construction
[edit]
Suppose two perpendicular lines are given, with intersection point O. For concreteness we may assume that these are the coordinate axes and that O is the origin, that is (0, 0). Let points Q = (q, 0) and R = (0, r) move on the axes in such a way that q + r = b, a constant. On the line QR, extended as necessary, mark points P and P' at a fixed distance a from Q. The locus of the points P and P' is Dürer's conchoid.[1]
Equation
[edit]The equation of the conchoid in Cartesian form is
In parametric form the equation is given by
where the parameter t is measured in radians.[2]
Properties
[edit]The curve has two components, asymptotic to the lines .[3] Each component is a rational curve. If a > b there is a loop, if a = b there is a cusp at (0,a).
Special cases include:
- a = 0: the line y = 0;
- b = 0: the line pair together with the circle ;
-
a = 3, b = 1, loop shown
-
a = 3, b = 3, cusp shown
-
a = 3, b = 5
The envelope of straight lines used in the construction form a parabola (as seen in Durer's original diagram above) and therefore the curve is a point-glissette formed by a line and one of its points sliding respectively against a parabola and one of its tangents.[4]
History
[edit]It was first described by the German painter and mathematician Albrecht Dürer (1471–1528) in his book Underweysung der Messung (Instruction in Measurement with Compass and Straightedge p. 38), calling it Ein muschellini (Conchoid or Shell). Dürer only drew one branch of the curve.
See also
[edit]References
[edit]- ^ Lawrence, J. Dennis (1972), A catalog of special plane curves, Dover Publications, p. 157, ISBN 0-486-60288-5
- ^ "Dürer's Conchoid". beware that the constants a and b are interchanged in this source
- ^ Fettis, Henry E. (1983), "The Geometry of Dürer's Conchoid" (PDF), Crux Mathematicorum, 9 (2), ISSN 0705-0348
- ^ Lockwood, E. H. (2007) [1967], A Book of Curves, Cambridge University Press, p. 164, ISBN 9780521044448