Cuboctahedron

Cuboctahedron
(Click here for rotating model)
Type	Archimedean solid Uniform polyhedron
Elements	F = 14, E = 24, V = 12 (χ = 2)
Faces by sides	8{3}+6{4}
Conway notation	aC aaT
Schläfli symbols	r{4,3} or ${\begin{Bmatrix}4\\3\end{Bmatrix}}$ rr{3,3} or $r{\begin{Bmatrix}3\\3\end{Bmatrix}}$
Schläfli symbols	t₁{4,3} or t_0,2{3,3}
Wythoff symbol	2 \| 3 4 3 3 \| 2
Coxeter diagram	or or
Symmetry group	O_h, B₃, [4,3], (432), order 48 T_d, [3,3], (332), order 24
Rotation group	O, [4,3]⁺, (432), order 24
Dihedral angle	$\operatorname {arcsec} \left(-{\sqrt {3}}\right)\approx 125.26^{\circ }$
References	U₀₇, C₁₉, W₁₁
Properties	Semiregular convex quasiregular
Colored faces	3.4.3.4 (Vertex figure)
Rhombic dodecahedron (dual polyhedron)	Net

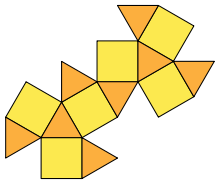
A cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasi-regular polyhedron, i.e. an Archimedean solid (vertex-uniform) with in addition edge-uniformity.

Its dual polyhedron is the rhombic dodecahedron.

Other Names

Heptaparallelohedron (Buckminster Fuller) [1]
- Fuller applied the name "Dymaxion"[2] and Vector Equilibrium [3] to this shape.
Rectified cube or rectified octahedron - ([[Norman Johnson (mathematician)

|Norman Johnson]])

- Also cantellated tetrahedron by a lower symmetry.

Area and volume

The area A and the volume V of the cuboctahedron of edge length a are:

A=(6+2{\sqrt {3}})a^{2}

V={\begin{matrix}{5 \over 3}\end{matrix}}{\sqrt {2}}a^{3}

Geometric relations

A cuboctahedron can be obtained by taking an appropriate cross section of a four-dimensional cross-polytope.

A cuboctahedron has octahedral symmetry. Its first stellation is the compound of a cube and its dual octahedron, with the vertices of the cuboctahedron located at the midpoints of the edges of either.

The cuboctahedron is a rectified cube and also a rectified octahedron.

It is also a cantellated tetrahedron. With this construction it is given the Wythoff Symbol: 3 3 | 2.

A skew cantellation of the tetrahedron produces a solid with faces parallel to those of the cuboctahedron, namely eight triangles of two sizes, and six rectangles. While its edges are unequal, this solid remains vertex-uniform: the solid has the full tetrahedral symmetry group and its vertices are equivalent under that group.

The edges of a cuboctahedron form four regular hexagons. If the cuboctahedron is cut in the plane of one of these hexagons, each half is a triangular cupola, one of the Johnson solids; the cuboctahedron itself thus can also be called a triangular gyrobicupola, the simplest of a series (other than the gyrobifastigium or "digonal gyrobicupola"). If the halves are put back together with a twist, so that triangles meet triangles and squares meet squares, the result is another Johnson solid, the triangular orthobicupola.

Both triangular bicupolae are important in sphere packing. The distance from the solid's centre to its vertices is equal to its edge length. Each central sphere can have up to twelve neighbors, and in a face-centered cubic lattice these take the positions of a cuboctahedron's vertices. In a hexagonal close-packed lattice they correspond to the corners of the triangular orthobicupola. In both cases the central sphere takes the position of the solid's centre.

Cuboctahedra appear as cells in three of the convex uniform honeycombs and in nine of the convex uniform polychora.

The volume of the cuboctahedron is 5/6 of that of the enclosing cube and 5/8 of that of the enclosing octahedron; it is 5/3 √2 times the cube of the length of an edge.

Cartesian coordinates

The Cartesian coordinates for the vertices of a cuboctahedron (of edge length √2) centered at the origin are

(±1,±1,0)

(±1,0,±1)

(0,±1,±1)

Related polyhedra

Compare:

Cube

Truncated cube

cuboctahedron

Truncated octahedron

Octahedron

References

Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)

External links

The Uniform Polyhedra
Virtual Reality Polyhedra The Encyclopedia of Polyhedra