Drag coefficient

In fluid dynamics, the drag coefficient (commonly denoted as: , or ) is a dimensionless quantity that is used to quantify the drag or resistance of an object in a fluid environment, such as air or water. It is used in the drag equation in which a lower drag coefficient indicates the object will have less aerodynamic or hydrodynamic drag. The drag coefficient is always associated with a particular surface area.[3]
The drag coefficient of any object comprises the effects of the two basic contributors to fluid dynamic drag: skin friction and form drag. The drag coefficient of a lifting airfoil or hydrofoil also includes the effects of lift-induced drag.[4][5] The drag coefficient of a complete structure such as an aircraft also includes the effects of interference drag.[6][7]
Definition
[edit]
The drag coefficient is defined as
where:
- is the drag force, which is by definition the force component in the direction of the flow velocity;[9]
- is the mass density of the fluid;[10]
- is the flow speed of the object relative to the fluid;
- is the reference area
The reference area depends on what type of drag coefficient is being measured. For automobiles and many other objects, the reference area is the projected frontal area of the vehicle. This may not necessarily be the cross-sectional area of the vehicle, depending on where the cross-section is taken. For example, for a sphere (note this is not the surface area = ).
For airfoils, the reference area is the nominal wing area. Since this tends to be large compared to the frontal area, the resulting drag coefficients tend to be low, much lower than for a car with the same drag, frontal area, and speed.
Airships and some bodies of revolution use the volumetric drag coefficient, in which the reference area is the square of the cube root of the airship volume (volume to the two-thirds power). Submerged streamlined bodies use the wetted surface area.
Two objects having the same reference area moving at the same speed through a fluid will experience a drag force proportional to their respective drag coefficients. Coefficients for unstreamlined objects can be 1 or more, for streamlined objects much less.
As a caution, note that although the above is the conventional definition for the drag coefficient, there are other definitions that one may encounter in the literature. The reason for this is that the conventional definition makes the most sense when one is in the Newton regime, such as what happens at high Reynolds number, where it makes sense to scale the drag to the momentum flux into the frontal area of the object. But, there are other flow regimes. In particular at very low Reynolds number, it is more natural to write the drag force as being proportional to a drag coefficient multiplied by the speed of the object (rather than the square of the speed of the object). An example of such a regime is the study of the mobility of aerosol particulates, such as smoke particles. This leads to a different formal definition of the "drag coefficient," of course.
Cauchy momentum equation
[edit]In the non dimensional form of the Cauchy momentum equation, the skin drag coefficient or skin friction coefficient is referred to the transversal area (the area normal to the drag force, so the coefficient is locally defined as:
where:
- is the local shear stress, which is by definition the stress component in the direction of the local flow velocity;[11]
- is the local dynamic pressure of the fluid
- is the local mass density of the fluid;[12]
- is the local flow speed of the fluid
Background
[edit]
and in the lower configuration
The drag equation
is essentially a statement that the drag force on any object is proportional to the density of the fluid and proportional to the square of the relative flow speed between the object and the fluid. The factor of comes from the dynamic pressure of the fluid, which is equal to the kinetic energy density.
The value of is not a constant but varies as a function of flow speed, flow direction, object position, object size, fluid density and fluid viscosity. Speed, kinematic viscosity and a characteristic length scale of the object are incorporated into a dimensionless quantity called the Reynolds number . is thus a function of . In a compressible flow, the speed of sound is relevant, and is also a function of Mach number .
For certain body shapes, the drag coefficient only depends on the Reynolds number , Mach number and the direction of the flow. For low Mach number , the drag coefficient is independent of Mach number. Also, the variation with Reynolds number within a practical range of interest is usually small, while for cars at highway speed and aircraft at cruising speed, the incoming flow direction is also more-or-less the same. Therefore, the drag coefficient can often be treated as a constant.[13]
For a streamlined body to achieve a low drag coefficient, the boundary layer around the body must remain attached to the surface of the body for as long as possible, causing the wake to be narrow. A high form drag results in a broad wake. The boundary layer will transition from laminar to turbulent if Reynolds number of the flow around the body is sufficiently great. Larger velocities, larger objects, and lower viscosities contribute to larger Reynolds numbers.[14]
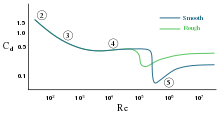
•2: attached flow (Stokes flow) and steady separated flow,
•3: separated unsteady flow, having a laminar flow boundary layer upstream of the separation, and producing a vortex street,
•4: separated unsteady flow with a laminar boundary layer at the upstream side, before flow separation, with downstream of the sphere a chaotic turbulent wake,
•5: post-critical separated flow, with a turbulent boundary layer.
For other objects, such as small particles, one can no longer consider that the drag coefficient is constant, but certainly is a function of Reynolds number.[15][16][17] At a low Reynolds number, the flow around the object does not transition to turbulent but remains laminar, even up to the point at which it separates from the surface of the object. At very low Reynolds numbers, without flow separation, the drag force is proportional to instead of ; for a sphere this is known as Stokes' law. The Reynolds number will be low for small objects, low velocities, and high viscosity fluids.[14]
A equal to 1 would be obtained in a case where all of the fluid approaching the object is brought to rest, building up stagnation pressure over the whole front surface. The top figure shows a flat plate with the fluid coming from the right and stopping at the plate. The graph to the left of it shows equal pressure across the surface. In a real flat plate, the fluid must turn around the sides, and full stagnation pressure is found only at the center, dropping off toward the edges as in the lower figure and graph. Only considering the front side, the of a real flat plate would be less than 1; except that there will be suction on the backside: a negative pressure (relative to ambient). The overall of a real square flat plate perpendicular to the flow is often given as 1.17.[citation needed] Flow patterns and therefore for some shapes can change with the Reynolds number and the roughness of the surfaces.
Drag coefficient examples
[edit]General
[edit]In general, is not an absolute constant for a given body shape. It varies with the speed of airflow (or more generally with Reynolds number ). A smooth sphere, for example, has a that varies from high values for laminar flow to 0.47 for turbulent flow. Although the drag coefficient decreases with increasing , the drag force increases.
| cd | Item[18] |
|---|---|
| 0.001 | Laminar flat plate parallel to the flow () |
| 0.005 | Turbulent flat plate parallel to the flow () |
| 0.1 | Smooth sphere () |
| 0.47 | Rough sphere () |
| 0.81 | Triangular trapeze (45°) |
| 0.9-1.7 | Trapeze with triangular basis (45°) |
| 0.295 | Bullet (not ogive, at subsonic velocity) |
| 1.0–1.1 | Skier |
| 1.0–1.3 | Wires and cables |
| 1.0–1.3 | Adult human (upright position) |
| 1.1-1.3 | Ski jumper[19] |
| 1.28 | Flat plate perpendicular to flow (3D)[20] |
| 1.3–1.5 | Empire State Building |
| 1.8–2.0 | Eiffel Tower |
| 1.98–2.05 | Long flat plate perpendicular to flow (2D) |
Aircraft
[edit]As noted above, aircraft use their wing area as the reference area when computing , while automobiles (and many other objects) use projected frontal area; thus, coefficients are not directly comparable between these classes of vehicles. In the aerospace industry, the drag coefficient is sometimes expressed in drag counts where 1 drag count = 0.0001 of a .[21]
| cd | Drag Count | Aircraft type[22] |
|---|---|---|
| 0.021 | 210 | F-4 Phantom II (subsonic) |
| 0.022 | 220 | Learjet 24 |
| 0.024 | 240 | Boeing 787[23] |
| 0.0265 | 265 | Airbus A380[24] |
| 0.027 | 270 | Cessna 172/182 |
| 0.027 | 270 | Cessna 310 |
| 0.031 | 310 | Boeing 747 |
| 0.044 | 440 | F-4 Phantom II (supersonic) |
| 0.048 | 480 | F-104 Starfighter |
Automobile
[edit]Blunt and streamlined body flows
[edit]Concept
[edit]The force between a fluid and a body, when there is relative motion, can only be transmitted by normal pressure and tangential friction stresses. So, for the whole body, the drag part of the force, which is in-line with the approaching fluid motion, is composed of frictional drag (viscous drag) and pressure drag (form drag). The total drag and component drag forces can be related as follows:
where:
- is the planform area of the body,
- is the wet surface of the body,
- is the pressure drag coefficient,
- is the friction drag coefficient,
- is the unit vector in the direction of the shear stress acting on the body surface dS,
- is the unit vector in the direction perpendicular to the body surface dS, pointing from the fluid to the solid,
- magnitude of the shear stress acting on the body surface dS,
- is the pressure far away from the body (note that this constant does not affect the final result),
- is pressure at surface dS,
- is the unit vector in direction of free stream flow
Therefore, when the drag is dominated by a frictional component, the body is called a streamlined body; whereas in the case of dominant pressure drag, the body is called a blunt or bluff body. Thus, the shape of the body and the angle of attack determine the type of drag. For example, an airfoil is considered as a body with a small angle of attack by the fluid flowing across it. This means that it has attached boundary layers, which produce much less pressure drag.
The wake produced is very small and drag is dominated by the friction component. Therefore, such a body (here an airfoil) is described as streamlined, whereas for bodies with fluid flow at high angles of attack, boundary layer separation takes place. This mainly occurs due to adverse pressure gradients at the top and rear parts of an airfoil.
Due to this, wake formation takes place, which consequently leads to eddy formation and pressure loss due to pressure drag. In such situations, the airfoil is stalled and has higher pressure drag than friction drag. In this case, the body is described as a blunt body.
A streamlined body looks like a fish (tuna), Oropesa, etc. or an airfoil with small angle of attack, whereas a blunt body looks like a brick, a cylinder or an airfoil with high angle of attack. For a given frontal area and velocity, a streamlined body will have lower resistance than a blunt body. Cylinders and spheres are taken as blunt bodies because the drag is dominated by the pressure component in the wake region at high Reynolds number.
To reduce this drag, either the flow separation could be reduced or the surface area in contact with the fluid could be reduced (to reduce friction drag). This reduction is necessary in devices like cars, bicycle, etc. to avoid vibration and noise production.
See also
[edit]- Automotive aerodynamics
- Automobile drag coefficient
- Ballistic coefficient
- Drag crisis
- Zero-lift drag coefficient
Notes
[edit]- ^ Baker, W.E. (1983). Explosion Hazards and Evaluation, Volume 5. Elsevier Science. ISBN 978-0-444-59988-9.
- ^ AARØNÆS, ANTON STADE (2014). Dynamic response of pipe rack steel structures to explosion loads (PDF). CHALMERS UNIVERSITY OF TECHNOLOGY.
- ^ McCormick, Barnes W. (1979). Aerodynamics, Aeronautics, and Flight Mechanics. New York: John Wiley & Sons, Inc. p. 24. ISBN 0-471-03032-5.
- ^ Clancy, L. J. (1975). "5.18". Aerodynamics. Wiley. ISBN 978-0-470-15837-1.
- ^ Abbott, Ira H., and Von Doenhoff, Albert E.: Theory of Wing Sections. Sections 1.2 and 1.3
- ^ "Modern Drag Equation". Wright.nasa.gov. 2010-03-25. Archived from the original on 2011-03-02. Retrieved 2010-12-07.
- ^ Clancy, L. J.: Aerodynamics. Section 11.17
- ^ Hoerner, Sighard F. (1965). Fluid-Dynamic Drag : Practical Information on Aerodynamic Drag and Hydrodynamic Resistance (2 ed.). p. 3–17.
- ^ See lift force and vortex induced vibration for a possible force components transverse to the flow direction
- ^ Note that for the Earth's atmosphere, the air density can be found using the barometric formula. Air is 1.293 kg/m3 at 0 °C (32 °F) and 1 atmosphere.
- ^ See lift force and vortex induced vibration for a possible force components transverse to the flow direction
- ^ Note that for the Earth's atmosphere, the air density can be found using the barometric formula. Air is 1.293 kg/m3 at 0 °C (32 °F) and 1 atmosphere.
- ^ Clancy, L. J.: Aerodynamics. Sections 4.15 and 5.4
- ^ a b Clancy, L. J.: Aerodynamics. Section 4.17
- ^ Clift R., Grace J. R., Weber M. E.: Bubbles, drops, and particles. Academic Press NY (1978).
- ^ Briens C. L.: Powder Technology. 67, 1991, 87-91.
- ^ Haider A., Levenspiel O.: Powder Technology. 58, 1989, 63-70.
- ^ Shapes
- ^ "Drag Coefficient". Engineeringtoolbox.com. Archived from the original on 2010-12-04. Retrieved 2010-12-07.
- ^ "Shape Effects on Drag". NASA. Archived from the original on 2013-02-16. Retrieved 2013-03-11.
- ^ Basha, W. A. and Ghaly, W. S., "Drag Prediction in Transitional Flow over Airfoils," Journal of Aircraft, Vol. 44, 2007, p. 824–32.
- ^ "Ask Us – Drag Coefficient & Lifting Line Theory". Aerospaceweb.org. 2004-07-11. Retrieved 2010-12-07.
- ^ "Boeing 787 Dreamliner : Analysis". Lissys.demon.co.uk. 2006-06-21. Archived from the original on 2010-08-13. Retrieved 2010-12-07.
- ^ "Airbus A380" (PDF). 2005-05-02. Archived (PDF) from the original on 2015-09-23. Retrieved 2014-10-06.
References
[edit]- L. J. Clancy (1975): Aerodynamics. Pitman Publishing Limited, London, ISBN 0-273-01120-0
- Abbott, Ira H., and Von Doenhoff, Albert E. (1959): Theory of Wing Sections. Dover Publications Inc., New York, Standard Book Number 486-60586-8
- Hoerner, Dr. Sighard F., Fluid-Dynamic Drag, Hoerner Fluid Dynamics, Bricktown New Jersey, 1965.
- Bluff Body: http://user.engineering.uiowa.edu/~me_160/lecture_notes/Bluff%20Body2.pdf
- Drag of Blunt Bodies and Streamlined Bodies: http://www.princeton.edu/~asmits/Bicycle_web/blunt.html
- Hucho, W.H., Janssen, L.J., Emmelmann, H.J. 6(1975): The optimization of body details-A method for reducing the aerodynamics drag. SAE 760185.


































