GPS signals


| Geodesy |
|---|
 |
GPS signals are broadcast by Global Positioning System satellites to enable satellite navigation. Receivers on or near the Earth's surface can determine location, time, and velocity using this information. The GPS satellite constellation is operated by the 2nd Space Operations Squadron (2SOPS) of Space Delta 8, United States Space Force.
GPS signals include ranging signals, which are used to measure the distance to the satellite, and navigation messages. The navigation messages include ephemeris data which are used both in trilateration to calculate the position of each satellite in orbit and also to provide information about the time and status of the entire satellite constellation, called the almanac.
There are four GPS signal specifications designed for civilian use. In order of date of introduction, these are: L1 C/A, L2C, L5 and L1C.[1] L1 C/A is also called the legacy signal and is broadcast by all currently operational satellites. L2C, L5 and L1C are modernized signals and are only broadcast by newer satellites (or not yet at all). Furthermore, as of January 2021[update], none of these three signals are yet considered to be fully operational for civilian use. In addition to the four aforementioned signals, there are restricted signals with published frequencies and chip rates, but the signals use encrypted coding, restricting use to authorized parties. Some limited use of restricted signals can still be made by civilians without decryption; this is called codeless and semi-codeless access, and this is officially supported.[2][3]
The interface to the User Segment (GPS receivers) is described in the Interface Control Documents (ICD). The format of civilian signals is described in the Interface Specification (IS) which is a subset of the ICD.
Common characteristics
[edit]The GPS satellites (called space vehicles in the GPS interface specification documents) transmit simultaneously several ranging codes and navigation data using binary phase-shift keying (BPSK). Only a limited number of central frequencies are used. Satellites using the same frequency are distinguished by using different ranging codes. In other words, GPS uses code-division multiple access. The ranging codes are also called chipping codes (in reference to CDMA/DSSS), pseudorandom noise and pseudorandom binary sequences (in reference to the fact that the sequences are predictable yet that they statistically resemble noise).
Some satellites transmit several BPSK streams at the same frequency in quadrature, in a form of quadrature amplitude modulation. However, unlike typical QAM systems where a single bit stream is split into two, half-symbol-rate bit streams to improve spectral efficiency, the in-phase and quadrature components of GPS signals are modulated by separate (but functionally related) bit streams.
Satellites are uniquely identified by a serial number called space vehicle number (SVN) which does not change during its lifetime. In addition, all operating satellites are numbered with a space vehicle identifier (SV ID) and pseudorandom noise number (PRN number) which uniquely identifies the ranging codes that a satellite uses. There is a fixed one-to-one correspondence between SV identifiers and PRN numbers described in the interface specification.[4] Unlike SVNs, the SV ID/PRN number of a satellite may be changed (resulting in a change to the ranging codes it uses). That is, no two active satellites can share any one active SV ID/PRN number. The current SVNs and PRN numbers for the GPS constellation are published at NAVCEN.
Legacy GPS signals
[edit]The original GPS design contains two ranging codes: the coarse/acquisition (C/A) code, which is freely available to the public, and the restricted precision (P) code, usually reserved for military applications.
Frequency information
[edit]
For the ranging codes and navigation message to travel from the satellite to the receiver, they must be modulated onto a carrier wave. In the case of the original GPS design, two frequencies are utilized; one at 1575.42 MHz (10.23 MHz × 154) called L1; and a second at 1227.60 MHz (10.23 MHz × 120), called L2.
The C/A code is transmitted on the L1 frequency as a 1.023 MHz signal using a bi-phase shift keying (BPSK) modulation technique. The P(Y)-code is transmitted on both the L1 and L2 frequencies as a 10.23 MHz signal using the same BPSK modulation, however the P(Y)-code carrier is in quadrature with the C/A carrier (meaning it is 90° out of phase).
Besides redundancy and increased resistance to jamming, a critical benefit of having two frequencies transmitted from one satellite is the ability to measure directly, and therefore remove, the ionospheric delay error for that satellite. Without such a measurement, a GPS receiver must use a generic model or receive ionospheric corrections from another source (such as the Wide Area Augmentation System or WAAS). Advances in the technology used on both the GPS satellites and the GPS receivers has made ionospheric delay the largest remaining source of error in the signal. A receiver capable of performing this measurement can be significantly more accurate and is typically referred to as a dual frequency receiver.
Modulation codes
[edit]Coarse/acquisition code
[edit]The C/A PRN codes are Gold codes with a period of 1023 chips transmitted at 1.023 Mchip/s, causing the code to repeat every 1 millisecond. They are exclusive-ored with a 50 bit/s navigation message and the result phase modulates the carrier as previously described. These codes only match up, or strongly autocorrelate when they are almost exactly aligned. Each satellite uses a unique PRN code, which does not correlate well with any other satellite's PRN code. In other words, the PRN codes are highly orthogonal to one another. The 1 ms period of the C/A code corresponds to 299.8 km of distance, and each chip corresponds to a distance of 293 m. Receivers track these codes well within one chip of accuracy, so measurement errors are considerably smaller than 293 m.[by how much?]
The C/A codes are generated by combining (using "exclusive or") two bit streams, each generated by two different maximal period 10 stage linear-feedback shift registers (LFSR). Different codes are obtained by selectively delaying one of those bit streams. Thus:
- C/Ai(t) = A(t) ⊕ B(t-Di)
where:
- C/Ai is the code with PRN number i.
- A is the output of the first LFSR whose generator polynomial is x → x10 + x3 + 1, and initial state is 11111111112.
- B is the output of the second LFSR whose generator polynomial is x → x10 + x9 + x8 + x6 + x3 + x2 + 1 and initial state is also 11111111112.
- Di is a delay (by an integer number of periods) specific to each PRN number i; it is designated in the GPS interface specification.[4]
- ⊕ is exclusive or.
The arguments of the functions therein are the number of bits or chips since their epochs, starting at 0. The epoch of the LFSRs is the point at which they are at the initial state; and for the overall C/A codes it is the start of any UTC second plus any integer number of milliseconds. The output of LFSRs at negative arguments is defined consistent with the period which is 1,023 chips (this provision is necessary because B may have a negative argument using the above equation).
The delay for PRN numbers 34 and 37 is the same; therefore their C/A codes are identical and are not transmitted at the same time[5] (it may make one or both of those signals unusable due to mutual interference depending on the relative power levels received on each GPS receiver).
Precision code
[edit]The P-code is a PRN sequence much longer than the C/A code: 6.187104 x 1012 chips. Even though the P-code chip rate (10.23 Mchip/s) is ten times that of the C/A code, it repeats only once per week, eliminating range ambiguity. It was assumed that receivers could not directly acquire such a long and fast code so they would first "bootstrap" themselves with the C/A code to acquire the spacecraft ephemerides, produce an approximate time and position fix, and then acquire the P-code to refine the fix.
Whereas the C/A PRNs are unique for each satellite, each satellite transmits a different segment of a master P-code sequence approximately 2.35 x 1014 chips long (235,000,000,000,000 chips). Each satellite repeatedly transmits its assigned segment of the master code, restarting every Sunday at 00:00:00 GPS time. For reference, the GPS epoch was Sunday January 6, 1980 at 00:00:00 UTC, but GPS does not follow UTC exactly because GPS time does not incorporate leap seconds. Thus, GPS time is ahead of UTC by an integer (whole) number of seconds.
The P code is public, so to prevent unauthorized users from using or potentially interfering with it through spoofing, the P-code is XORed with W-code, a cryptographically generated sequence, to produce the Y-code. The Y-code is what the satellites have been transmitting since the anti-spoofing module was enabled. The encrypted signal is referred to as the P(Y)-code.
The details of the W-code are secret, but it is known that it is applied to the P-code at approximately 500 kHz,[6] about 20 times slower than the P-code chip rate. This has led to semi-codeless approaches for tracking the P(Y) signal without knowing the W-code.
Navigation message
[edit]| Sub- frame |
Word | Description |
|---|---|---|
| 1 | 1–2 | Telemetry and handover words (TLM and HOW) |
| 3–10 | Satellite clock, GPS time relationship | |
| 2–3 | 1–2 | Telemetry and handover words (TLM and HOW) |
| 3–10 | Ephemeris (precise satellite orbit) | |
| 4–5 | 1–2 | Telemetry and handover words (TLM and HOW) |
| 3–10 | Almanac component (satellite network synopsis, error correction) |
In addition to the PRN ranging codes, a receiver needs to know the time and position of each active satellite. GPS encodes this information into the navigation message and modulates it onto both the C/A and P(Y) ranging codes at 50 bit/s. The navigation message format described in this section is called LNAV data (for legacy navigation).
The navigation message conveys information of three types:
- The GPS date and time, and the satellite's status.
- The ephemeris: precise orbital information for the transmitting satellite.
- The almanac: status and low-resolution orbital information for every satellite.
An ephemeris is valid for only four hours, while an almanac is valid–with little dilution of precision–for up to two weeks.[7] The receiver uses the almanac to acquire a set of satellites based on stored time and location. As the receiver acquires each satellite, each satellite’s ephemeris is decoded so that the satellite can be used for navigation.
The navigation message consists of 30-second frames 1,500 bits long, divided into five 6-second subframes of ten 30-bit words each. Each subframe has the GPS time in 6-second increments. Subframe 1 contains the GPS date (week number), satellite clock correction information, satellite status and satellite health. Subframes 2 and 3 together contain the transmitting satellite's ephemeris data. Subframes 4 and 5 contain page 1 through 25 of the 25-page almanac. The almanac is 15,000 bits long and takes 12.5 minutes to transmit.
A frame begins at the start of the GPS week and every 30 seconds thereafter. Each week begins with the transmission of almanac page 1.[8]
There are two navigation message types: LNAV-L is used by satellites with PRN numbers 1 to 32 (called lower PRN numbers) and LNAV-U is used by satellites with PRN numbers 33 to 63 (called upper PRN numbers).[9] The two types use very similar formats. Subframes 1 to 3 are the same,[10] while subframes 4 and 5 are almost the same. Each message type contains almanac data for all satellites using the same navigation message type but not the other.
Each subframe begins with a Telemetry Word (TLM), which enables the receiver to detect the beginning of a subframe and determine the receiver clock time at which the navigation subframe begins. Next is the handover word (HOW) giving the GPS time (as the time for when the first bit of the next subframe will be transmitted) and identifies the specific subframe within a complete frame.[11][12] The remaining eight words of the subframe contain the actual data specific to that subframe. Each word includes 6 bits of parity generated using an algorithm based on Hamming codes, which take into account the 24 non-parity bits of that word and the last 2 bits of the previous word.
After a subframe has been read and interpreted, the time the next subframe was sent can be calculated through the use of the clock correction data and the HOW. The receiver knows the receiver clock time of when the beginning of the next subframe was received from detection of the Telemetry Word thereby enabling computation of the transit time and thus the pseudorange.
Time
[edit]GPS time is expressed with a resolution of 1.5 seconds as a week number and a time of week count (TOW).[13] Its zero point (week 0, TOW 0) is defined to be 1980-01-06T00:00Z. The TOW count is a value ranging from 0 to 403,199 whose meaning is the number of 1.5 second periods elapsed since the beginning of the GPS week. Expressing TOW count thus requires 19 bits (219 = 524,288). GPS time is a continuous time scale in that it does not include leap seconds; therefore the start/end of GPS weeks may differ from that of the corresponding UTC day by an integer (whole) number of seconds.
In each subframe, each hand-over word (HOW) contains the most significant 17 bits of the TOW count corresponding to the start of the next following subframe.[14] Note that the 2 least significant bits can be safely omitted because one HOW occurs in the navigation message every 6 seconds, which is equal to the resolution of the truncated TOW count thereof. Equivalently, the truncated TOW count is the time duration since the last GPS week start/end to the beginning of the next frame in units of 6 seconds.
Each frame contains (in subframe 1) the 10 least significant bits of the corresponding GPS week number.[15] Note that each frame is entirely within one GPS week because GPS frames do not cross GPS week boundaries.[16] Since rollover occurs every 1,024 GPS weeks (approximately every 19.6 years; 1,024 is 210), a receiver that computes current calendar dates needs to deduce the upper week number bits or obtain them from a different source. One possible method is for the receiver to save its current date in memory when shut down, and when powered on, assume that the newly decoded truncated week number corresponds to the period of 1,024 weeks that starts at the last saved date. This method correctly deduces the full week number if the receiver is never allowed to remain shut down (or without a time and position fix) for more than 1,024 weeks (~19.6 years).
Almanac
[edit]The almanac consists of coarse orbit and status information for each satellite in the constellation, an ionospheric model, and information to relate GPS derived time to Coordinated Universal Time (UTC). Each frame contains a part of the almanac (in subframes 4 and 5) and the complete almanac is transmitted by each satellite in 25 frames total (requiring 12.5 minutes).[17] The almanac serves several purposes. The first is to assist in the acquisition of satellites at power-up by allowing the receiver to generate a list of visible satellites based on stored position and time, while an ephemeris from each satellite is needed to compute position fixes using that satellite. In older hardware, lack of an almanac in a new receiver would cause long delays before providing a valid position, because the search for each satellite was a slow process. Advances in hardware have made the acquisition process much faster, so not having an almanac is no longer an issue. The second purpose is for relating time derived from the GPS (called GPS time) to the international time standard of UTC. Finally, the almanac allows a single-frequency receiver to correct for ionospheric delay error by using a global ionospheric model. The corrections are not as accurate as GNSS augmentation systems like WAAS or dual-frequency receivers. However, it is often better than no correction, since ionospheric error is the largest error source for a single-frequency GPS receiver.
Structure of subframes 4 and 5
[edit]
|
|
Data updates
[edit]Satellite data is updated typically every 24 hours, with up to 60 days data loaded in case there is a disruption in the ability to make updates regularly. Typically the updates contain new ephemerides, with new almanacs uploaded less frequently. The Control Segment guarantees that during normal operations a new almanac will be uploaded at least every 6 days.
Satellites broadcast a new ephemeris every two hours. The ephemeris is generally valid for 4 hours, with provisions for updates every 4 hours or longer in non-nominal conditions. The time needed to acquire the ephemeris is becoming a significant element of the delay to first position fix, because as the receiver hardware becomes more capable, the time to lock onto the satellite signals shrinks; however, the ephemeris data requires 18 to 36 seconds before it is received, due to the low data transmission rate.
Modernization and additional GPS signals
[edit]Having reached full operational capability on July 17, 1995[20] the GPS system had completed its original design goals. However, additional advances in technology and new demands on the existing system led to the effort to "modernize" the GPS system. Announcements from the Vice President and the White House in 1998 heralded the beginning of these changes, and in 2000, the U.S. Congress reaffirmed the effort, referred to as GPS III.
The project involves new ground stations and new satellites, with additional navigation signals for both civilian and military users. It aims to improve the accuracy and availability for all users. The implementation goal of 2013 was established, and contractors were offered incentives if they could complete it by 2011.
General features
[edit]
Modernized GPS civilian signals have two general improvements over their legacy counterparts: a dataless acquisition aid and forward error correction (FEC) coding of the NAV message.
A dataless acquisition aid is an additional signal, called a pilot carrier in some cases, broadcast alongside the data signal. This dataless signal is designed to be easier to acquire than the data encoded and, upon successful acquisition, can be used to acquire the data signal. This technique improves acquisition of the GPS signal and boosts power levels at the correlator.
The second advancement is to use forward error correction (FEC) coding on the NAV message itself. Due to the relatively slow transmission rate of NAV data (usually 50 bits per second), small interruptions can have potentially large impacts. Therefore, FEC on the NAV message is a significant improvement in overall signal robustness.
L2C
[edit]One of the first announcements was the addition of a new civilian-use signal, to be transmitted on a frequency other than the L1 frequency used for the coarse/acquisition (C/A) signal. Ultimately, this became the L2C signal, so called because it is broadcast on the L2 frequency. Because it requires new hardware on board the satellite, it is only transmitted by the so-called Block IIR-M and later design satellites. The L2C signal is tasked with improving accuracy of navigation, providing an easy to track signal, and acting as a redundant signal in case of localized interference. L2C signals have been broadcast beginning in April 2014 on satellites capable of broadcasting it, but are still considered pre-operational.[1] As of January 2021[update], L2C is broadcast on 23 satellites and is expected on 24 satellites by 2023.[1]
Unlike the C/A code, L2C contains two distinct PRN code sequences to provide ranging information; the civil-moderate code (called CM), and the civil-long length code (called CL). The CM code is 10,230 chips long, repeating every 20 ms. The CL code is 767,250 chips long, repeating every 1,500 ms. Each signal is transmitted at 511,500 chips per second (chip/s); however, they are multiplexed together to form a 1,023,000-chip/s signal.
CM is modulated with the CNAV Navigation Message (see below), whereas CL does not contain any modulated data and is called a dataless sequence. The long, dataless sequence provides for approximately 24 dB greater correlation (~250 times stronger) than L1 C/A-code.
When compared to the C/A signal, L2C has 2.7 dB greater data recovery and 0.7 dB greater carrier-tracking, although its transmission power is 2.3 dB weaker.
The current status of the L2C signal as of July 3, 2023[21] is:
- Pre-operational signal with message set "healthy"
- Broadcasting from 25 GPS satellites (as of July 3, 2023)
- Began launching in 2005 with GPS Block IIR-M
- Available on 24 GPS satellites with ground segment control capability by 2023 (as of Jan 2020)
CM and CL codes
[edit]The civil-moderate and civil-long ranging codes are generated by a modular LFSR which is reset periodically to a predetermined initial state. The period of the CM and CL is determined by this resetting and not by the natural period of the LFSR (as is the case with the C/A code). The initial states are designated in the interface specification and are different for different PRN numbers and for CM/CL. The feedback polynomial/mask is the same for CM and CL. The ranging codes are thus given by:
- CMi(t) = A(Xi,t mod 10 230)
- CLi(t) = A(Yi,t mod 767 250)
where:
- CMi and CLi are the ranging codes for PRN number i and their arguments are the integer number of chips elapsed (starting at 0) since start/end of GPS week, or equivalently since the origin of the GPS time scale (see § Time).
- A(x, t) is the output of the LFSR when initialized with initial state x after being clocked t times.
- Xi and Yi are the initial states for CM and CL respectively. for PRN number .
- mod is the remainder of division operation.
- t is the integer number of CM and CL chip periods since the origin of GPS time or equivalently, since any GPS second (starting from 0).
The initial states are described in the GPS interface specification as numbers expressed in octal following the convention that the LFSR state is interpreted as the binary representation of a number where the output bit is the least significant bit, and the bit where new bits are shifted in is the most significant bit. Using this convention, the LFSR shifts from most significant bit to least significant bit and when seen in big endian order, it shifts to the right. The states called final state in the IS are obtained after 10229 cycles for CM and after 767249 cycles for LM (just before reset in both cases).
CNAV navigation message
[edit]| Bits[23] | Information |
|---|---|
| 1–8 | Preamble |
| 9–14 | PRN of transmitting satellite |
| 15–20 | Message type ID |
| 21–37 | Truncated TOW count[24] |
| 38 | Alert flag |
| 277–300 | Cyclic redundancy check |
| Type ID | Description |
|---|---|
| 10–11 | Ephemeris and health |
| 12, 31, 37 | Almanac parameters |
| 13–14, 34 | Differential correction |
| 15, 36 | Text messages |
| 30 | Ionospheric and group delay correction |
| 32 | Earth orientation parameters |
| 33 | UTC parameters |
| 35 | GPS/GNSS time offset |
The CNAV data is an upgraded version of the original NAV navigation message. It contains higher precision representation and nominally more accurate data than the NAV data. The same type of information (time, status, ephemeris, and almanac) is still transmitted using the new CNAV format; however, instead of using a frame / subframe architecture, it uses a new pseudo-packetized format made of 12-second 300-bit messages analogous to LNAV frames. While LNAV frames have a fixed information content, CNAV messages may be of one of several defined types. The type of a frame determines its information content. Messages do not follow a fixed schedule regarding which message types will be used, allowing the Control Segment some versatility. However, for some message types there are lower bounds on how often they will be transmitted.
In CNAV, at least 1 out of every 4 packets are ephemeris data and the same lower bound applies for clock data packets.[25] The design allows for a wide variety of packet types to be transmitted. With a 32-satellite constellation, and the current requirements of what needs to be sent, less than 75% of the bandwidth is used. Only a small fraction of the available packet types have been defined; this enables the system to grow and incorporate advances without breaking compatibility.
There are many important changes in the new CNAV message:
- It uses forward error correction (FEC) provided by a rate 1/2 convolutional code, so while the navigation message is 25-bit/s, a 50-bit/s signal is transmitted.
- Messages carry a 24-bit CRC, against which integrity can be checked.
- The GPS week number is now represented as 13 bits, or 8192 weeks, and only repeats every 157.0 years, meaning the next return to zero won't occur until the year 2137. This is longer compared to the L1 NAV message's use of a 10-bit week number, which returns to zero every 19.6 years.
- There is a packet that contains a GPS-to-GNSS time offset. This allows better interoperability with other global time-transfer systems, such as Galileo and GLONASS, both of which are supported.
- The extra bandwidth enables the inclusion of a packet for differential correction, to be used in a similar manner to satellite based augmentation systems and which can be used to correct the L1 NAV clock data.
- Every packet contains an alert flag, to be set if the satellite data can not be trusted. This means users will know within 12 seconds if a satellite is no longer usable. Such rapid notification is important for safety-of-life applications, such as aviation.
- Finally, the system is designed to support 63 satellites, compared with 32 in the L1 NAV message.
CNAV messages begin and end at start/end of GPS week plus an integer multiple of 12 seconds.[26] Specifically, the beginning of the first bit (with convolution encoding already applied) to contain information about a message matches the aforesaid synchronization. CNAV messages begin with an 8-bit preamble which is a fixed bit pattern and whose purpose is to enable the receiver to detect the beginning of a message.
Forward error correction code
[edit]The convolutional code used to encode CNAV is described by:
where:
- and are the unordered outputs of the convolutional encoder
- is the raw (non FEC encoded) navigation data, consisting of the simple concatenation of the 300-bit messages.
- is the integer number of non FEC encoded navigation data bits elapsed since an arbitrary point in time (starting at 0).
- is the FEC encoded navigation data.
- is the integer number of FEC encoded navigation data bits elapsed since the same epoch than (likewise starting at 0).
Since the FEC encoded bit stream runs at 2 times the rate than the non FEC encoded bit as already described, then . FEC encoding is performed independently of navigation message boundaries;[27] this follows from the above equations.
L2C frequency information
[edit]An immediate effect of having two civilian frequencies being transmitted is the civilian receivers can now directly measure the ionospheric error in the same way as dual frequency P(Y)-code receivers. However, users utilizing the L2C signal alone, can expect 65% more position uncertainty due to ionospheric error than with the L1 signal alone.[28]
Military (M-code)
[edit]A major component of the modernization process is a new military signal. Called the Military code, or M-code, it was designed to further improve the anti-jamming and secure access of the military GPS signals.
Very little has been published about this new, restricted code. It contains a PRN code of unknown length transmitted at 5.115 MHz. Unlike the P(Y)-code, the M-code is designed to be autonomous, meaning that a user can calculate their position using only the M-code signal. From the P(Y)-code's original design, users had to first lock onto the C/A code and then transfer the lock to the P(Y)-code. Later, direct-acquisition techniques were developed that allowed some users to operate autonomously with the P(Y)-code.
MNAV navigation message
[edit]A little more is known about the new navigation message, which is called MNAV. Similar to the new CNAV, this new MNAV is packeted instead of framed, allowing for very flexible data payloads. Also like CNAV it can utilize Forward Error Correction (FEC) and advanced error detection (such as a CRC).
M-code frequency information
[edit]The M-code is transmitted in the same L1 and L2 frequencies already in use by the previous military code, the P(Y)-code. The new signal is shaped to place most of its energy at the edges (away from the existing P(Y) and C/A carriers). It does not work at every satellite, and M-code was switched off for SVN62/PRN25 on 5 April 2011.[29]
In a major departure from previous GPS designs, the M-code is intended to be broadcast from a high-gain directional antenna, in addition to a full-Earth antenna. This directional antenna's signal, called a spot beam, is intended to be aimed at a specific region (several hundred kilometers in diameter) and increase the local signal strength by 20 dB, or approximately 100 times stronger. A side effect of having two antennas is that the GPS satellite will appear to be two GPS satellites occupying the same position to those inside the spot beam. While the whole Earth M-code signal is available on the Block IIR-M satellites, the spot beam antennas will not be deployed until the Block III satellites are deployed, which began in December 2018.
An interesting side effect of having each satellite transmit four separate signals is that the MNAV can potentially transmit four different data channels, offering increased data bandwidth.
The modulation method is binary offset carrier, using a 10.23 MHz subcarrier against the 5.115 MHz code. This signal will have an overall bandwidth of approximately 24 MHz, with significantly separated sideband lobes. The sidebands can be used to improve signal reception.
L5
[edit]The L5 signal provides a means of radionavigation secure and robust enough for life critical applications, such as aircraft precision approach guidance. The signal is broadcast in a frequency band protected by the ITU for aeronautical radionavigation services. It was first demonstrated from satellite USA-203 (Block IIR-M), and is available on all satellites from GPS IIF and GPS III. L5 signals have been broadcast beginning in April 2014 on satellites that support it.[1]
The status of the L5 signal as of July 3, 2023[update] is:[30]
- Pre-operational signal with message set "unhealthy" until sufficient monitoring capability established
- Broadcasting from 18 GPS satellites
- Scheduled to be available on 24 GPS satellites by approximately 2027
The L5 band provides additional robustness in the form of interference mitigation, the band being internationally protected, redundancy with existing bands, geostationary satellite augmentation, and ground-based augmentation. The added robustness of this band also benefits terrestrial applications.[31]
Two PRN ranging codes are transmitted on L5 in quadrature: the in-phase code (called I5-code) and the quadrature-phase code (called Q5-code). Both codes are 10,230 chips long, transmitted at 10.23 Mchip/s (1 ms repetition period), and are generated identically (differing only in initial states). Then, I5 is modulated (by exclusive-or) with navigation data (called L5 CNAV) and a 10-bit Neuman-Hofman code clocked at 1 kHz. Similarly, the Q5-code is then modulated but with only a 20-bit Neuman-Hofman code that is also clocked at 1 kHz.
Compared to L1 C/A and L2, these are some of the changes in L5:
- Improved signal structure for enhanced performance
- Higher transmitted power than L1/L2 signal (~3 dB, or 2× as powerful)
- Wider bandwidth provides a 10× processing gain, provides sharper autocorrelation (in absolute terms, not relative to chip time duration) and requires a higher sampling rate at the receiver.
- Longer spreading codes (10× longer than C/A)
- Uses the Aeronautical Radionavigation Services band
I5 and Q5 codes
[edit]The I5-code and Q5-code are generated using the same structure but with different parameters. These codes are the combination (by exclusive-or) of the output of 2 differing linear-feedback shift registers (LFSRs) which are selectively reset.
- 5i(t) = U(t) ⊕ Vi(t)
- U(t) = XA((t mod 10 230) mod 8 190)
- Vi(t) = XBi(Xi, t mod 10 230)
where:
- i is an ordered pair (P, n) where P ∈ {I, Q} for in-phase and quadrature-phase, and n a PRN number; both phases and a single PRN are required for the L5 signal from a single satellite.
- 5i is the ranging codes for i; also denoted as I5n and Q5n.
- U and Vi are intermediate codes, with U not depending on phase or PRN.
- The output of two 13-stage LFSRs with clock state t' is used:
- XA(x,t') has feedback polynomial x13 + x12 + x10 + x9 + 1, and initial state 11111111111112.
- XBi(x,t') has feedback polynomial x13 + x12 + x8 + x7 + x6 + x4 + x3 + x + 1, and initial state Xi.
- Xi is the initial state specified for the phase and PRN number given by i (designated in the IS[32]).
- t is the integer number of chip periods since the origin of GPS time or equivalently, since any GPS second (starting from 0).
A and B are maximal length LFSRs. The modulo operations correspond to resets. Note that both are reset each millisecond (synchronized with C/A code epochs). In addition, the extra modulo operation in the description of A is due to the fact it is reset 1 cycle before its natural period (which is 8,191) so that the next repetition becomes offset by 1 cycle with respect to B[33] (otherwise, since both sequences would repeat, I5 and Q5 would repeat within any 1 ms period as well, degrading correlation characteristics).
L5 navigation message
[edit]The L5 CNAV data includes SV ephemerides, system time, SV clock behavior data, status messages and time information, etc. The 50 bit/s data is coded in a rate 1/2 convolution coder. The resulting 100 symbols per second (sps) symbol stream is modulo-2 added to the I5-code only; the resultant bit-train is used to modulate the L5 in-phase (I5) carrier. This combined signal is called the L5 Data signal. The L5 quadrature-phase (Q5) carrier has no data and is called the L5 Pilot signal. The format used for L5 CNAV is very similar to that of L2 CNAV. One difference is that it uses 2 times the data rate. The bit fields within each message,[34] message types, and forward error correction code algorithm are the same as those of L2 CNAV. L5 CNAV messages begin and end at start/end of GPS week plus an integer multiple of 6 seconds (this applies to the beginning of the first bit to contain information about a message, as is the case for L2 CNAV).[35]
L5 frequency information
[edit]Broadcast on the L5 frequency (1176.45 MHz, 10.23 MHz × 115), which is an aeronautical navigation band. The frequency was chosen so that the aviation community can manage interference to L5 more effectively than L2.[35]
L1C
[edit]L1C is a civilian-use signal, to be broadcast on the L1 frequency (1575.42 MHz), which contains the C/A signal used by all current GPS users. The L1C signals will be broadcast from GPS III and later satellites, the first of which was launched in December 2018.[1] As of January 2021[update], L1C signals are not yet broadcast, and only four operational satellites are capable of broadcasting them. L1C is expected on 24 GPS satellites in the late 2020s.[1]
L1C consists of a pilot (called L1CP) and a data (called L1CD) component.[36] These components use carriers with the same phase (within a margin of error of 100 milliradians), instead of carriers in quadrature as with L5.[37] The PRN codes are 10,230 chips long and transmitted at 1.023 Mchip/s, thus repeating in 10 ms. The pilot component is also modulated by an overlay code called L1CO (a secondary code that has a lower rate than the ranging code and is also predefined, like the ranging code).[36] Of the total L1C signal power, 25% is allocated to the data and 75% to the pilot. The modulation technique used is BOC(1,1) for the data signal and TMBOC for the pilot. The time multiplexed binary offset carrier (TMBOC) is BOC(1,1) for all except 4 of 33 cycles, when it switches to BOC(6,1).
- Implementation will provide C/A code to ensure backward compatibility
- Assured of 1.5 dB increase in minimum C/A code power to mitigate any noise floor increase
- Data-less signal component pilot carrier improves tracking compared with L1 C/A
- Enables greater civil interoperability with Galileo L1
The current status of the L1C signal as of July 3, 2023[21] is:
- Developmental signal with message set "unhealthy" and no navigation data
- Broadcasting from 6 GPS satellites (as of July 3, 2023)
- Began launching in 2018 with GPS III
- Available on 24 GPS satellites in late 2020s
L1C ranging code
[edit]The L1C pilot and data ranging codes are based on a Legendre sequence with length 10223 used to build an intermediate code (called a Weil code) which is expanded with a fixed 7-bit sequence to the required 10,230 bits. This 10,230-bit sequence is the ranging code and varies between PRN numbers and between the pilot and data components. The ranging codes are described by:[38]
where:
- is the ranging code for PRN number and component .
- represents a period of ; it is introduced only to allow a more clear notation. To obtain a direct formula for start from the right side of the formula for and replace all instances of with .
- is the integer number of L1C chip periods (which is 1⁄1.023 μs) since the origin of GPS time or equivalently, since any GPS second (starting from 0).
- is an ordered pair identifying a PRN number and a code (L1CP or L1CD) and is of the form or where is the PRN number of the satellite, and are symbols (not variables) that indicate the L1CP code or L1CD code, respectively.
- is an intermediate code: a Legendre sequence whose domain is the set of integers for which .
- is an intermediate code called Weil code, with the same domain as .
- is a 7-bit long sequence defined for 0-based indexes 0 to 6.
- is the 0-based insertion index of the sequence into the ranging code (specific for PRN number and code ). It is defined in the Interface Specification (IS) as a 1-based index , therefore .[39]
- is the Weil index for PRN number and code designated in the IS.[39]
- is the remainder of division (or modulo) operation, which differs to the notation in statements of modular congruence, also used in this article.
According to the formula above and the GPS IS, the first bits (equivalently, up to the insertion point of ) of and are the first bits the corresponding Weil code; the next 7 bits are ; the remaining bits are the remaining bits of the Weil code.
The IS asserts that .[40] For clarity, the formula for does not account for the hypothetical case in which , which would cause the instance of inserted into to wrap from index 10229 to 0.
L1C overlay code
[edit]The overlay codes are 1,800 bits long and is transmitted at 100 bit/s, synchronized with the navigation message encoded in L1CD.
For PRN numbers 1 to 63 they are the truncated outputs of maximal period LFSRs which vary in initial conditions and feedback polynomials.[41]
For PRN numbers 64 to 210 they are truncated Gold codes generated by combining 2 LFSR outputs ( and , where is the PRN number) whose initial state varies. has one of the 4 feedback polynomials used overall (among PRN numbers 64–210). has the same feedback polynomial for all PRN numbers in the range 64–210.[42]
CNAV-2 navigation message
[edit]| Subframe | Bit count | Description | |
|---|---|---|---|
| Raw | Encoded | ||
| 1 | 9 | 52 | Time of interval (TOI) |
| 2 | 576 | 1,200 | Time correction and ephemeris data |
| 3 | 250 | 548 | Variable data |
| Page no. | Description |
|---|---|
| 1 | UTC & IONO |
| 2 | GGTO & EOP |
| 3 | Reduced almanac |
| 4 | Midi almanac |
| 5 | Differential correction |
| 6 | Text |
The L1C navigation data (called CNAV-2) is broadcast in 1,800 bits long (including FEC) frames and is transmitted at 100 bit/s.
The frames of L1C are analogous to the messages of L2C and L5. While L2 CNAV and L5 CNAV use a dedicated message type for ephemeris data, all CNAV-2 frames include that information.
The common structure of all messages consists of 3 frames, as listed in the adjacent table. The content of subframe 3 varies according to its page number which is analogous to the type number of L2 CNAV and L5 CNAV messages. Pages are broadcast in an arbitrary order.[43]
The time of messages (not to be confused with clock correction parameters) is expressed in a different format than the format of the previous civilian signals. Instead it consists of 3 components:
- The week number, with the same meaning as with the other civilian signals. Each message contains the week number modulo 8,192 or equivalently, the 13 least significant bits of the week number, allowing direct specification of any date within a cycling 157-year range.
- An interval time of week (ITOW): the integer number of 2 hour periods elapsed since the latest start/end of week. It has range 0 to 83 (inclusive), requiring 7 bits to encode.
- A time of interval (TOI): the integer number of 18 second periods elapsed since the period represented by the current ITOW to the beginning of the next message. It has range 0 to 399 (inclusive) and requires 9 bits of data.
TOI is the only content of subframe 1. The week number and ITOW are contained in subframe 2 along with other information.
Subframe 1 is encoded by a modified BCH code. Specifically, the 8 least significant bits are BCH encoded to generate 51 bits, then combined using exclusive or with the most significant bit and finally the most significant bit is appended as the most significant bit of the previous result to obtain the final 52 bits.[44] Subframes 2 and 3 are individually expanded with a 24-bit CRC, then individually encoded using a low-density parity-check code, and then interleaved as a single unit using a block interleaver.[45]
Overview of frequencies
[edit]| Band | Frequency (MHz) |
Phase | Original usage | Modernized usage |
|---|---|---|---|---|
| L1 | 1575.42 (10.23 × 154) |
I | Encrypted precision P(Y) code | |
| Q | Coarse/acquisition (C/A) code | C/A, L1 Civilian (L1C), and Military (M) code | ||
| L2 | 1227.60 (10.23 × 120) |
I | Encrypted precision P(Y) code | |
| Q | unmodulated carrier | L2 Civilian (L2C) code and Military (M) code | ||
| L3 | 1381.05 (10.23 × 135) |
used by Nuclear Detonation (NUDET) Detection System Payload (NDS): signals nuclear detonations/ high-energy infrared events. Used to enforce nuclear test ban treaties. |
||
| L4 | 1379.9133... (10.23 × 1214/9) |
— | being studied for additional ionospheric correction[46]: 607 | |
| L5 | 1176.45 (10.23 × 115) |
I | — | Safety-of-Life (SoL) Data signal |
| Q | Safety-of-Life (SoL) Pilot signal | |||
All satellites broadcast at the same two frequencies, 1.57542 GHz (L1 signal) and 1.2276 GHz (L2 signal). The satellite network uses a CDMA spread-spectrum technique where the low-bitrate message data is encoded with a high-rate pseudo-random noise (PRN) sequence that is different for each satellite. The receiver must be aware of the PRN codes for each satellite to reconstruct the actual message data. The C/A code, for civilian use, transmits data at 1.023 million chips per second, whereas the P code, for U.S. military use, transmits at 10.23 million chips per second. The L1 carrier is modulated by both the C/A and P codes, while the L2 carrier is only modulated by the P code.[47] The P code can be encrypted as a so-called P(Y) code which is only available to military equipment with a proper decryption key. Both the C/A and P(Y) codes impart the precise time-of-day to the user.
Each composite signal (in-phase and quadrature phase) becomes:
where and represent signal powers; and represent codes with/without data . This is a formula for the ideal case (which is not attained in practice) as it does not model timing errors, noise, amplitude mismatch between components or quadrature error (when components are not exactly in quadrature).
Demodulation and decoding
[edit]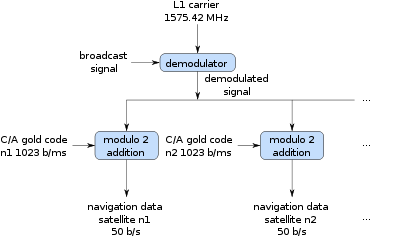
A GPS receiver processes the GPS signals received on its antenna to determine position, velocity and/or timing. The signal at antenna is amplified, down converted to baseband or intermediate frequency, filtered (to remove frequencies outside the intended frequency range for the digital signal that would alias into it) and digitalized; these steps may be chained in a different order. Note that aliasing is sometimes intentional (specifically, when undersampling is used) but filtering is still required to discard frequencies not intended to be present in the digital representation.
For each satellite used by the receiver, the receiver must first acquire the signal and then track it as long as that satellite is in use; both are performed in the digital domain in by far most (if not all) receivers.
Acquiring a signal is the process of determining the frequency and code phase (both relative to receiver time) when it was previously unknown. Code phase must be determined within an accuracy that depends on the receiver design (especially the tracking loop); 0.5 times the duration of code chips (approx. 0.489 μs) is a representative value.
Tracking is the process of continuously adjusting the estimated frequency and phase to match the received signal as close as possible and therefore is a phase locked loop. Note that acquisition is performed to start using a particular satellite, but tracking is performed as long as that satellite is in use.
In this section, one possible procedure is described for L1 C/A acquisition and tracking, but the process is very similar for the other signals. The described procedure is based on computing the correlation of the received signal with a locally generated replica of the ranging code and detecting the highest peak or lowest valley. The offset of the highest peak or lowest valley contains information about the code phase relative to receiver time. The duration of the local replica is set by receiver design and is typically shorter than the duration of navigation data bits, which is 20 ms.
Acquisition
[edit]Acquisition of a given PRN number can be conceptualized as searching for a signal in a bidimensional search space where the dimensions are (1) code phase, (2) frequency. In addition, a receiver may not know which PRN number to search for, and in that case a third dimension is added to the search space: (3) PRN number.
- Frequency space
- The frequency range of the search space is the band where the signal may be located given the receiver knowledge. The carrier frequency varies by roughly 5 kHz due to the Doppler effect when the receiver is stationary; if the receiver moves, the variation is higher. The code frequency deviation is 1/1,540 times the carrier frequency deviation for L1 because the code frequency is 1/1,540 of the carrier frequency (see § Frequencies used by GPS). The down conversion does not affect the frequency deviation; it only shifts all the signal frequency components down. Since the frequency is referenced to the receiver time, the uncertainty in the receiver oscillator frequency adds to the frequency range of the search space.
- Code phase space
- The ranging code has a period of 1,023 chips each of which lasts roughly 0.977 μs (see § Coarse/acquisition code). The code gives strong autocorrelation only at offsets less than 1 in magnitude. The extent of the search space in the code phase dimension depends on the granularity of the offsets at which correlation is computed. It is typical to search for the code phase within a granularity of 0.5 chips or finer; that means 2,046 offsets. There may be more factors increasing the size of the search space of code phase. For example, a receiver may be designed so as to examine 2 consecutive windows of the digitalized signal, so that at least one of them does not contain a navigation bit transition (which worsens the correlation peak); this requires the signal windows to be at most 10 ms long.
- PRN number space
- The lower PRN numbers range from 1 to 32 and therefore there are 32 PRN numbers to search for when the receiver does not have information to narrow the search in this dimension. The higher PRN numbers range from 33 to 66. See § Navigation message.
If the almanac information has previously been acquired, the receiver picks which satellites to listen for by their PRNs. If the almanac information is not in memory, the receiver enters a search mode and cycles through the PRN numbers until a lock is obtained on one of the satellites. To obtain a lock, it is necessary that there be an unobstructed line of sight from the receiver to the satellite. The receiver can then decode the almanac and determine the satellites it should listen for. As it detects each satellite's signal, it identifies it by its distinct C/A code pattern.
Simple correlation
[edit]The simplest way to acquire the signal (not necessarily the most effective or least computationally expensive) is to compute the dot product of a window of the digitalized signal with a set of locally generated replicas. The locally generated replicas vary in carrier frequency and code phase to cover all the already mentioned search space which is the Cartesian product of the frequency search space and the code phase search space. The carrier is a complex number where real and imaginary components are both sinusoids as described by Euler's formula. The replica that generates the highest magnitude of dot product is likely the one that best matches the code phase and frequency of the signal; therefore, if that magnitude is above a threshold, the receiver proceeds to track the signal or further refine the estimated parameters before tracking. The threshold is used to minimize false positives (apparently detecting a signal when there is in fact no signal), but some may still occur occasionally.
Using a complex carrier allows the replicas to match the digitalized signal regardless of the signal's carrier phase and to detect that phase (the principle is the same used by the Fourier transform). The dot product is a complex number; its magnitude represents the level of similarity between the replica and the signal, as with an ordinary correlation of real-valued time series. The argument of the dot product is an approximation of the corresponding carrier in the digitalized signal.
As an example, assume that the granularity for the search in code phase is 0.5 chips and in frequency is 500 Hz, then there are 1,023/0.5 = 2,046 code phases and 10,000 Hz/500 Hz = 20 frequencies to try for a total of 20×2,046 = 40,920 local replicas. Note that each frequency bin is centered on its interval and therefore covers 250 Hz in each direction; for example, the first bin has a carrier at −4.750 Hz and covers the interval −5,000 Hz to −4,500 Hz. Code phases are equivalent modulo 1,023 because the ranging code is periodic; for example, phase −0.5 is equivalent to phase 1,022.5.
The following table depicts the local replicas that would be compared against the digitalized signal in this example. "•" means a single local replica while "..." is used for elided local replicas:
| Carrier freq. deviation |
Code phase (in chips) | ||||
|---|---|---|---|---|---|
| 0.0 | 0.5 | (more phases) | 1,022.0 | 1,022.5 | |
| −4,750 Hz | • | • | ... | • | • |
| −4,250 Hz | • | • | ... | • | • |
| (more frequencies) |
... | ... | ... | ... | ... |
| 4,250 Hz | • | • | ... | • | • |
| 4,750 Hz | • | • | ... | • | • |
Fourier transform
[edit]As an improvement over the simple correlation method, it is possible to implement the computation of dot products more efficiently with a Fourier transform. Instead of performing one dot product for each element in the Cartesian product of code and frequency, a single operation involving FFT and covering all frequencies is performed for each code phase; each such operation is more computationally expensive, but it may still be faster overall than the previous method due to the efficiency of FFT algorithms, and it recovers carrier frequency with a higher accuracy, because the frequency bins are much closely spaced in a DFT.
Specifically, for all code phases in the search space, the digitalized signal window is multiplied element by element with a local replica of the code (with no carrier), then processed with a discrete Fourier transform.
Given the previous example to be processed with this method, assume real-valued data (as opposed to complex data, which would have in-phase and quadrature components), a sampling rate of 5 MHz, a signal window of 10 ms, and an intermediate frequency of 2.5 MHz. There will be 5 MHz×10 ms = 50,000 samples in the digital signal, and therefore 25,001 frequency components ranging from 0 Hz to 2.5 MHz in steps of 100 Hz (note that the 0 Hz component is real because it is the average of a real-valued signal and the 2.5 MHz component is real as well because it is the critical frequency). Only the components (or bins) within 5 kHz of the central frequency are examined, which is the range from 2.495 MHz to 2.505 MHz, and it is covered by 51 frequency components. There are 2,046 code phases as in the previous case, thus in total 51×2,046 = 104,346 complex frequency components will be examined.
Circular correlation with Fourier transform
[edit]Likewise, as an improvement over the simple correlation method, it is possible to perform a single operation covering all code phases for each frequency bin. The operation performed for each code phase bin involves forward FFT, element-wise multiplication in the frequency domain. inverse FFT, and extra processing so that overall, it computes circular correlation instead of circular convolution. This yields more accurate code phase determination than the simple correlation method in contrast with the previous method, which yields more accurate carrier frequency determination than the previous method.
Tracking and navigation message decoding
[edit]Since the carrier frequency received can vary due to Doppler shift, the points where received PRN sequences begin may not differ from O by an exact integral number of milliseconds. Because of this, carrier frequency tracking along with PRN code tracking are used to determine when the received satellite's PRN code begins.[48] Unlike the earlier computation of offset in which trials of all 1,023 offsets could potentially be required, the tracking to maintain lock usually requires shifting of half a pulse width or less. To perform this tracking, the receiver observes two quantities, phase error and received frequency offset. The correlation of the received PRN code with respect to the receiver generated PRN code is computed to determine if the bits of the two signals are misaligned. Comparisons of the received PRN code with receiver generated PRN code shifted half a pulse width early and half a pulse width late are used to estimate adjustment required.[49] The amount of adjustment required for maximum correlation is used in estimating phase error. Received frequency offset from the frequency generated by the receiver provides an estimate of phase rate error. The command for the frequency generator and any further PRN code shifting required are computed as a function of the phase error and the phase rate error in accordance with the control law used. The Doppler velocity is computed as a function of the frequency offset from the carrier nominal frequency. The Doppler velocity is the velocity component along the line of sight of the receiver relative to the satellite.
As the receiver continues to read successive PRN sequences, it will encounter a sudden change in the phase of the 1,023-bit received PRN signal. This indicates the beginning of a data bit of the navigation message.[50] This enables the receiver to begin reading the 20 millisecond bits of the navigation message. The TLM word at the beginning of each subframe of a navigation frame enables the receiver to detect the beginning of a subframe and determine the receiver clock time at which the navigation subframe begins. The HOW word then enables the receiver to determine which specific subframe is being transmitted.[11][12] There can be a delay of up to 30 seconds before the first estimate of position because of the need to read the ephemeris data before computing the intersections of sphere surfaces.
After a subframe has been read and interpreted, the time the next subframe was sent can be calculated through the use of the clock correction data and the HOW. The receiver knows the receiver clock time of when the beginning of the next subframe was received from detection of the Telemetry Word thereby enabling computation of the transit time and thus the pseudorange. The receiver is potentially capable of getting a new pseudorange measurement at the beginning of each subframe or every 6 seconds.
Then the orbital position data, or ephemeris, from the navigation message is used to calculate precisely where the satellite was at the start of the message. A more sensitive receiver will potentially acquire the ephemeris data more quickly than a less sensitive receiver, especially in a noisy environment.[51]
See also
[edit]Sources and references
[edit]Bibliography
[edit]GPS Interface Specification
- "GPS Interface Specification (GPS-IS-200K)" (PDF). 4 March 2019. (describes L1, L2C and P).
- "GPS Interface Specification (GPS-IS-705F)" (PDF). 4 March 2019. (describes L5).
- "GPS Interface Specification (GPS-IS-800E)" (PDF). 4 March 2019. (describes L1C).
Notes
[edit]- ^ a b c d e f "New Civil Signals". Retrieved 2021-01-18.
- ^ "Codeless/Semi-Codeless GPS Access Commitments".
- ^ Civilian GPS Receivers Actually do Have Access to the L2 Frequency
- ^ a b GPS-IS-200, tables 3-Ia, 3-Ib (p. 6–8).
- ^ GPS-IS-200, § 3.2.1.3, table 3-Ia (p. 4, 7).
- ^ US patent 5576715, Litton, James D.; Russell, Graham & Woo, Richard K., "Method and apparatus for digital processing in a global positioning system receiver", issued 1996-11-19, assigned to Leica Geosystems
- ^ Petovello, Mark (November 2008). "Satellite Almanac Life Expectancy" (PDF). Inside GNSS: 14–19. Retrieved 17 July 2019.
- ^ GPS-IS-200, § 20.3.4.1 (p. 63–130).
- ^ GPS-IS-200, § 6.4.1 (p. 63–64).
- ^ GPS-IS-200, § 40.3.3 (p. 207).
- ^ a b "NAVSTAR GPS User Equipment Introduction" (PDF). US Government. Archived from the original (PDF) on 2013-10-21. Retrieved 2013-07-24. Section 1.4.2.6.
- ^ a b "Essentials of Satellite Navigation Compendium" (PDF). Archived from the original (PDF) on November 7, 2014.
- ^ GPS-IS-200, § 6.2.4 (p. 50), § 3.3.4 (p. 41).
- ^ GPS-IS-200, § 20.3.3.1 (p. 87).
- ^ GPS-IS-200, § 20.3.3.3.1.1 (p. 90).
- ^ GPS-IS-200, § 20.3.4.1 (p. 130).
- ^ "Interface Specification IS-GPS-200, Revision D: Navstar GPS Space Segment/Navigation User Interfaces" (PDF). Navstar GPS Joint Program Office. Archived from the original (PDF) on 2012-09-08. Retrieved 2013-07-24. Page 103.
- ^ GPS-IS-200, § 20.3.3.5.1 (p. 108–109).
- ^ GPS-IS-200, § 40.3.3.5.1 (p. 207–208).
- ^ US Coast Guard GPS FAQ
- ^ a b "GPS.gov: New Civil Signals". www.gps.gov. Retrieved 10 June 2021.
 This article incorporates text from this source, which is in the public domain.
This article incorporates text from this source, which is in the public domain.
- ^ GPS-IS-200, § 30.3.3 (p. 140).
- ^ Numbered starting from 1. Bit 1 is the first bit in the message and bit 300 is the last one.
- ^ TOW count for the beginning of the next message. It uses the same format than the truncated TOW in LNAV.
- ^ GPS-IS-200, § 30.3.4.1 (p. 190).
- ^ GPS-IS-200, § 3.3.3.1.1 (p. 39) Note that synchronization is described in the IS in terms of X1 epochs, which occur each 1.5 seconds and are synchronized with start/end of GPS week.
- ^ GPS-IS-200, § 3.3.3.1.1 (p. 39).
- ^ "Interface Specification IS-GPS-200 Revision D" (PDF). United States Coast Guard. 7 December 2004. Retrieved 2010-07-18.
- ^ "GPS Antennas Thrust". Retrieved 28 June 2022.
- ^ "GPS.gov: New Civil Signals". www.gps.gov. Retrieved 2024-02-16.
- ^ "Satellite Navigation - GPS - Policy - Modernization". FAA.gov. FAA. 13 November 2014. Retrieved 25 September 2018.
- ^ GPS-IS-705, tables 3-Ia, 3-Ib (p. 5 7).
- ^ GPS-IS-705, § 3.3.2.2 (p. 14).
- ^ GPS-IS-705, § 20.3.3 (p. 41).
- ^ a b GPS-IS-705, § 3.3.3.1.1 (p. 39).
- ^ a b GPS-IS-800, § 3.1 (p. 2–3).
- ^ GPS-IS-800, § 3.2.1.6.1 (p. 4).
- ^ The ranging codes are described in GPS-IS-800, § 3.2.2.1.1 (p. 7–8) using a different notation.
- ^ a b GPS-IS-800, table 3.2-2 (p. 10–12).
- ^ GPS-IS-800, p. 7.
- ^ GPS-IS-800, § 3.2.2.1 (p. 6).
- ^ GPS-IS-800, § 6.3.1.2 (p. 110–111).
- ^ GPS-IS-800, § 3.5.5.1 (p. 69).
- ^ GPS-IS-800, § 3.2.3.2 (p. 19–20).
- ^ GPS-IS-800, § 3.2.3.1 (p. 18).
- ^ Penttinen, Jyrki T. J. (16 March 2015). The Telecommunications Handbook: Engineering Guidelines for Fixed, Mobile and Satellite Systems. John Wiley & Sons. ISBN 9781119944881.
- ^ How GPS works. Konowa.de (2005).
- ^ "How a GPS Receiver Gets a Lock". Gpsinformation.net. Retrieved 2009-10-13.
- ^ "NAVSTAR GPS User Equipment Introduction" (PDF). US Government. Archived from the original (PDF) on 2013-10-21. Retrieved 2013-07-24. Section 1.4.2.4.
- ^ "NAVSTAR GPS User Equipment Introduction" (PDF). US Government. Archived from the original (PDF) on 2013-10-21. Retrieved 2013-07-24. Section 1.4.2.5.
- ^ "AN02 Network Assistance". Archived from the original on 2010-02-21. Retrieved 2007-09-10.






































