Hyperbolic motion (relativity)

Hyperbolic motion is the motion of an object with constant proper acceleration in special relativity. It is called hyperbolic motion because the equation describing the path of the object through spacetime is a hyperbola, as can be seen when graphed on a Minkowski diagram whose coordinates represent a suitable inertial (non-accelerated) frame. This motion has several interesting features, among them that it is possible to outrun a photon if given a sufficient head start, as may be concluded from the diagram.[1]
History[edit]
Hermann Minkowski (1908) showed the relation between a point on a worldline and the magnitude of four-acceleration and a "curvature hyperbola" (German: Krümmungshyperbel).[2] In the context of Born rigidity, Max Born (1909) subsequently coined the term "hyperbolic motion" (German: Hyperbelbewegung) for the case of constant magnitude of four-acceleration, then provided a detailed description for charged particles in hyperbolic motion, and introduced the corresponding "hyperbolically accelerated reference system" (German: hyperbolisch beschleunigtes Bezugsystem).[3] Born's formulas were simplified and extended by Arnold Sommerfeld (1910).[4] For early reviews see the textbooks by Max von Laue (1911, 1921)[5] or Wolfgang Pauli (1921).[6] See also Galeriu (2015)[7] or Gourgoulhon (2013),[8] and Acceleration (special relativity)#History.
Worldline[edit]
The proper acceleration of a particle is defined as the acceleration that a particle "feels" as it accelerates from one inertial reference frame to another. If the proper acceleration is directed parallel to the line of motion, it is related to the ordinary three-acceleration in special relativity by
where is the instantaneous speed of the particle, the Lorentz factor, is the speed of light, and is the coordinate time. Solving for the equation of motion gives the desired formulas, which can be expressed in terms of coordinate time as well as proper time . For simplification, all initial values for time, location, and velocity can be set to 0, thus:[5][6][9][10][11]
-
(1)
This gives , which is a hyperbola in time T and the spatial location variable . In this case, the accelerated object is located at at time . If instead there are initial values different from zero, the formulas for hyperbolic motion assume the form:[12][13][14]
Rapidity[edit]
The worldline for hyperbolic motion (which from now on will be written as a function of proper time) can be simplified in several ways. For instance, the expression
can be subjected to a spatial shift of amount , thus
- ,[15]
by which the observer is at position at time . Furthermore, by setting and introducing the rapidity ,[14] the equations for hyperbolic motion reduce to[4][16]
-
(2)
with the hyperbola .
Charged particles in hyperbolic motion[edit]
Born (1909),[3] Sommerfeld (1910),[4] von Laue (1911),[5] Pauli (1921)[6] also formulated the equations for the electromagnetic field of charged particles in hyperbolic motion.[7] This was extended by Hermann Bondi & Thomas Gold (1955)[17] and Fulton & Rohrlich (1960)[18][19]
This is related to the controversially[20][21] discussed question, whether charges in perpetual hyperbolic motion do radiate or not, and whether this is consistent with the equivalence principle – even though it's about an ideal situation, because perpetual hyperbolic motion is not possible. While early authors such as Born (1909) or Pauli (1921) argued that no radiation arises, later authors such as Bondi & Gold[17] and Fulton & Rohrlich[18][19] showed that radiation does indeed arise.
Proper reference frame[edit]
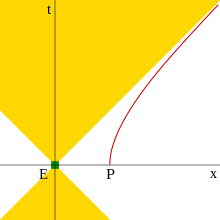
In equation (2) for hyperbolic motion, the expression was constant, whereas the rapidity was variable. However, as pointed out by Sommerfeld,[16] one can define as a variable, while making constant. This means, that the equations become transformations indicating the simultaneous rest shape of an accelerated body with hyperbolic coordinates as seen by a comoving observer
By means of this transformation, the proper time becomes the time of the hyperbolically accelerated frame. These coordinates, which are commonly called Rindler coordinates (similar variants are called Kottler-Møller coordinates or Lass coordinates), can be seen as a special case of Fermi coordinates or Proper coordinates, and are often used in connection with the Unruh effect. Using these coordinates, it turns out that observers in hyperbolic motion possess an apparent event horizon, beyond which no signal can reach them.
Special conformal transformation[edit]
A lesser known method for defining a reference frame in hyperbolic motion is the employment of the special conformal transformation, consisting of an inversion, a translation, and another inversion.[22] It is commonly interpreted as a gauge transformation in Minkowski space, though some authors alternatively use it as an acceleration transformation (see Kastrup for a critical historical survey).[23] It has the form
Using only one spatial dimension by , and further simplifying by setting , and using the acceleration , it follows[24]
with the hyperbola . It turns out that at the time becomes singular, to which Fulton & Rohrlich & Witten[24] remark that one has to stay away from this limit, while Kastrup[23] (who is very critical of the acceleration interpretation) remarks that this is one of the strange results of this interpretation.
Notes[edit]
- ^ Misner, Thorne & Wheeler 1973, Chapter 6.
- ^ Minkowski, Hermann (1909). [Wikisource translation: Space and Time]. Jahresbericht der Deutschen Mathematiker-Vereinigung. Leipzig.
- ^ a b Born, Max (1909). "Die Theorie des starren Elektrons in der Kinematik des Relativitätsprinzips" [Wikisource translation: The Theory of the Rigid Electron in the Kinematics of the Principle of Relativity]. Annalen der Physik. 335 (11): 1–56. Bibcode:1909AnP...335....1B. doi:10.1002/andp.19093351102.
- ^ a b c Sommerfeld, Arnold (1910). "Zur Relativitätstheorie II: Vierdimensionale Vektoranalysis" [Wikisource translation: On the Theory of Relativity II: Four-dimensional Vector Analysis]. Annalen der Physik. 338 (14): 649–689. Bibcode:1910AnP...338..649S. doi:10.1002/andp.19103381402.
- ^ a b c von Laue, M. (1921). Die Relativitätstheorie, Band 1 (fourth edition of "Das Relativitätsprinzip" ed.). Vieweg. pp. 89–90, 155–166.; First edition 1911, second expanded edition 1913, third expanded edition 1919.
- ^ a b c Pauli, Wolfgang (1921), "Die Relativitätstheorie", Encyclopädie der Mathematischen Wissenschaften, 5 (2): 539–776
In English: Pauli, W. (1981) [1921]. Theory of Relativity. Vol. 165. Dover Publications. ISBN 0-486-64152-X.{{cite book}}:|journal=ignored (help) - ^ a b Galeriu, C. (2017) [2015]. "Electric charge in hyperbolic motion: the early history". Archive for History of Exact Sciences. 71 (4): 1–16. arXiv:1509.02504. doi:10.1007/s00407-017-0191-x. S2CID 118510589.
- ^ Gourgoulhon, E. (2013). Special Relativity in General Frames: From Particles to Astrophysics. Springer. p. 396. ISBN 978-3642372766.
- ^ Møller, C. (1955). The theory of relativity. Oxford Clarendon Press. pp. 74–75.
- ^ Rindler, W. (1977). Essential Relativity. Springer. pp. 49–50. ISBN 354007970X.
- ^ PhysicsFAQ (2016), "Relativistic rocket", see external links
- ^ Gallant, J. (2012). Doing Physics with Scientific Notebook: A Problem Solving Approach. John Wiley & Sons. pp. 437–441. ISBN 978-0470665978.
- ^ Müller, T., King, A., & Adis, D. (2006). "A trip to the end of the universe and the twin "paradox"". American Journal of Physics. 76 (4): 360–373. arXiv:physics/0612126. Bibcode:2008AmJPh..76..360M. doi:10.1119/1.2830528. S2CID 42983285.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ a b Fraundorf, P. (2012). "A traveler-centered intro to kinematics": IV–B. arXiv:1206.2877. Bibcode:2012arXiv1206.2877F.
{{cite journal}}: Cite journal requires|journal=(help) - ^ Pauli (1921), p. 628, used the notation where
- ^ a b Sommerfeld (1910), pp. 670-671 used the form and with the imaginary angle and imaginary time .
- ^ a b Bondi, H., & Gold, T. (1955). "The field of a uniformly accelerated charge, with special reference to the problem of gravitational acceleration". Proceedings of the Royal Society of London. 229 (1178): 416–424. Bibcode:1955RSPSA.229..416B. doi:10.1098/rspa.1955.0098. S2CID 121563673.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ a b Fulton, Thomas; Rohrlich, Fritz (1960). "Classical radiation from a uniformly accelerated charge". Annals of Physics. 9 (4): 499–517. Bibcode:1960AnPhy...9..499F. doi:10.1016/0003-4916(60)90105-6.
- ^ a b Rohrlich, Fritz (1963). "The principle of equivalence". Annals of Physics. 22 (2): 169–191. Bibcode:1963AnPhy..22..169R. doi:10.1016/0003-4916(63)90051-4.
- ^ Stephen Lyle (2008). Uniformly Accelerating Charged Particles: A Threat to the Equivalence Principle. Springer. ISBN 978-3540684770.
- ^ Øyvind Grøn (2012). "Review Article: Electrodynamics of Radiating Charges". Advances in Mathematical Physics. 2012: 528631. doi:10.1155/2012/528631. hdl:10642/1380.
- ^ Galeriu, Cǎlin (2019) "Electric charge in hyperbolic motion: the special conformal solution", European Journal of Physics 40(6) doi:10.1088/1361-6404/ab3df6
- ^ a b Kastrup, H. A. (2008). "On the advancements of conformal transformations and their associated symmetries in geometry and theoretical physics". Annalen der Physik. 520 (9–10): 631–690. arXiv:0808.2730. Bibcode:2008AnP...520..631K. doi:10.1002/andp.200810324. S2CID 12020510.
- ^ a b Fulton, T., Rohrlich, F., & Witten, L. (1962). "Physical consequences of a co-ordinate transformation to a uniformly accelerating frame". Il Nuovo Cimento. 26 (4): 652–671. Bibcode:1962NCim...26..652F. doi:10.1007/BF02781794. S2CID 121467786.
{{cite journal}}: CS1 maint: multiple names: authors list (link)
References[edit]
- Leigh Page (Feb 1936). "A New Relativity. Paper I. Fundamental Principles and Transformations Between Accelerated Systems". Physical Review. 49 (3): 254–268. Bibcode:1936PhRv...49..254P. doi:10.1103/PhysRev.49.254.
- Leigh Page & Norman I. Adams (Mar 1936). "A New Relativity. Paper II. Transformation of the Electromagnetic Field Between Accelerated Systems and the Force Equation". Physical Review. 49 (6): 466–469. Bibcode:1936PhRv...49..466P. doi:10.1103/PhysRev.49.466.
- Misner, Charles W.; Thorne, Kip. S.; Wheeler, John A. (1973), Gravitation, W. H. Freeman, Chapter 6, ISBN 0-7167-0344-0
- Rindler Wolfgang (1960). "Hyperbolic Motion in Curved Space Time". Physical Review. 119 (6): 2082–2089. Bibcode:1960PhRv..119.2082R. doi:10.1103/PhysRev.119.2082.
- Ludwik Silberstein (1914): The Theory of Relativity, page 190.
- Naber, Gregory L., The Geometry of Minkowski Spacetime, Springer-Verlag, New York, 1992. ISBN 0-387-97848-8 (hardcover), ISBN 0-486-43235-1 (Dover paperback edition). pp 58–60.
External links[edit]
- Physics FAQ: The Relativistic Rocket
- Mathpages: Accelerated Travels, Does A Uniformly Accelerating Charge Radiate?

















![{\displaystyle {\scriptstyle {\begin{array}{c|c}{\begin{aligned}u(T)&={\frac {u_{0}\gamma _{0}+\alpha T}{\sqrt {1+\left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)^{2}}}}\quad \\&=c\tanh \left\{\operatorname {arsinh} \left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)\right\}\\X(T)&=X_{0}+{\frac {c^{2}}{\alpha }}\left({\sqrt {1+\left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)^{2}}}-\gamma _{0}\right)\\&=X_{0}+{\frac {c^{2}}{\alpha }}\left\{\cosh \left[\operatorname {arsinh} \left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)\right]-\gamma _{0}\right\}\\c\tau (T)&=c\tau _{0}+{\frac {c^{2}}{\alpha }}\ln \left({\frac {{\sqrt {c^{2}+\left(u_{0}\gamma _{0}+\alpha T\right){}^{2}}}+u_{0}\gamma _{0}+\alpha T}{\left(c+u_{0}\right)\gamma _{0}}}\right)\\&=c\tau _{0}+{\frac {c^{2}}{\alpha }}\left\{\operatorname {arsinh} \left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)-\operatorname {artanh} \left({\frac {u_{0}}{c}}\right)\right\}\end{aligned}}&{\begin{aligned}u(\tau )&=c\tanh \left\{\operatorname {artanh} \left({\frac {u_{0}}{c}}\right)+{\frac {\alpha \tau }{c}}\right\}\\\\X(\tau )&=X_{0}+{\frac {c^{2}}{\alpha }}\left\{\cosh \left[\operatorname {artanh} \left({\frac {u_{0}}{c}}\right)+{\frac {\alpha \tau }{c}}\right]-\gamma _{0}\right\}\\\\cT(\tau )&=cT_{0}+{\frac {c^{2}}{\alpha }}\left\{\sinh \left[\operatorname {artanh} \left({\frac {u_{0}}{c}}\right)+{\frac {\alpha \tau }{c}}\right]-{\frac {u_{0}\gamma _{0}}{c}}\right\}\end{aligned}}\end{array}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06b3bf81e2e1800bf5f97de52e2bc322b2f2ae18)

























