Information gain ratio
This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages)
|
In decision tree learning, information gain ratio is a ratio of information gain to the intrinsic information. It was proposed by Ross Quinlan,[1] to reduce a bias towards multi-valued attributes by taking the number and size of branches into account when choosing an attribute.[2]
Information gain is also known as mutual information.[3]
Information gain calculation
[edit]Information gain is the reduction in entropy produced from partitioning a set with attributes and finding the optimal candidate that produces the highest value:
where is a random variable and is the entropy of given the value of attribute .
The information gain is equal to the total entropy for an attribute if for each of the attribute values a unique classification can be made for the result attribute. In this case the relative entropies subtracted from the total entropy are 0.
Split information calculation
[edit]The split information value for a test is defined as follows:
where is a discrete random variable with possible values and being the number of times that occurs divided by the total count of events where is the set of events.
The split information value is a positive number that describes the potential worth of splitting a branch from a node. This in turn is the intrinsic value that the random variable possesses and will be used to remove the bias in the information gain ratio calculation.
Information gain ratio calculation
[edit]The information gain ratio is the ratio between the information gain and the split information value:
Example
[edit]Using weather data published by Fordham University,[4] the table was created below:
| Outlook | Temperature | Humidity | Wind | Play |
|---|---|---|---|---|
| Sunny | Hot | High | False | No |
| Sunny | Hot | High | True | No |
| Overcast | Hot | High | False | Yes |
| Rainy | Mild | High | False | Yes |
| Rainy | Cool | Normal | False | Yes |
| Rainy | Cool | Normal | True | No |
| Overcast | Cool | Normal | True | Yes |
| Sunny | Mild | High | False | No |
| Sunny | Cool | Normal | False | Yes |
| Rainy | Mild | Normal | False | Yes |
| Sunny | Mild | Normal | False | Yes |
| Overcast | Mild | High | True | Yes |
| Overcast | Hot | Normal | False | Yes |
| Rainy | Mild | High | True | No |
Using the table above, one can find the entropy, information gain, split information, and information gain ratio for each variable (outlook, temperature, humidity, and wind). These calculations are shown in the tables below:
|
|
|
|
Using the above tables, one can deduce that Outlook has the highest information gain ratio. Next, one must find the statistics for the sub-groups of the Outlook variable (sunny, overcast, and rainy), for this example one will only build the sunny branch (as shown in the table below):
| Outlook | Temperature | Humidity | Wind | Play |
|---|---|---|---|---|
| Sunny | Hot | High | False | No |
| Sunny | Hot | High | True | No |
| Sunny | Mild | High | False | No |
| Sunny | Cool | Normal | False | Yes |
| Sunny | Mild | Normal | True | Yes |
One can find the following statistics for the other variables (temperature, humidity, and wind) to see which have the greatest effect on the sunny element of the outlook variable:
|
|
|
Humidity was found to have the highest information gain ratio. One will repeat the same steps as before and find the statistics for the events of the Humidity variable (high and normal):
|
|
Since the play values are either all "No" or "Yes", the information gain ratio value will be equal to 1. Also, now that one has reached the end of the variable chain with Wind being the last variable left, they can build an entire root to leaf node branch line of a decision tree.
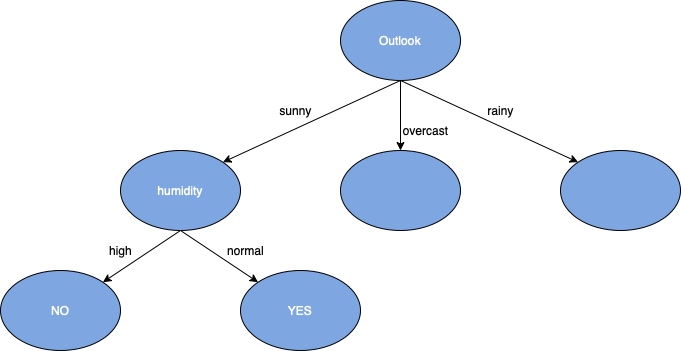
Once finished with reaching this leaf node, one would follow the same procedure for the rest of the elements that have yet to be split in the decision tree. This set of data was relatively small, however, if a larger set was used, the advantages of using the information gain ratio as the splitting factor of a decision tree can be seen more.
Advantages
[edit]Information gain ratio biases the decision tree against considering attributes with a large number of distinct values.
For example, suppose that we are building a decision tree for some data describing a business's customers. Information gain ratio is used to decide which of the attributes are the most relevant. These will be tested near the root of the tree. One of the input attributes might be the customer's telephone number. This attribute has a high information gain, because it uniquely identifies each customer. Due to its high amount of distinct values, this will not be chosen to be tested near the root.
Disadvantages
[edit]Although information gain ratio solves the key problem of information gain, it creates another problem. If one is considering an amount of attributes that have a high number of distinct values, these will never be above one that has a lower number of distinct values.
Difference from information gain
[edit]- Information gain's shortcoming is created by not providing a numerical difference between attributes with high distinct values from those that have less.
- Example: Suppose that we are building a decision tree for some data describing a business's customers. Information gain is often used to decide which of the attributes are the most relevant, so they can be tested near the root of the tree. One of the input attributes might be the customer's credit card number. This attribute has a high information gain, because it uniquely identifies each customer, but we do not want to include it in the decision tree: deciding how to treat a customer based on their credit card number is unlikely to generalize to customers we haven't seen before.
- Information gain ratio's strength is that it has a bias towards the attributes with the lower number of distinct values.
- Below is a table describing the differences of information gain and information gain ratio when put in certain scenarios.
| Information gain | Information gain ratio |
|---|---|
| Will not favor any attributes by number of distinct values | Will favor attribute that have a lower number of distinct values |
| When applied to attributes that can take on a large number of distinct values, this technique might learn the training set too well | User will struggle if required to find attributes requiring a high number of distinct values |
See also
[edit]References
[edit]- ^ Quinlan, J. R. (1986). "Induction of decision trees". Machine Learning. 1: 81–106. doi:10.1007/BF00116251.
- ^ http://www.ke.tu-darmstadt.de/lehre/archiv/ws0809/mldm/dt.pdf Archived 2014-12-28 at the Wayback Machine [bare URL PDF]
- ^ "Information gain, mutual information and related measures".
- ^ https://storm.cis.fordham.edu/~gweiss/data-mining/weka-data/weather.nominal.arff













