Inversive geometry
In geometry, inversive geometry is the study of inversion, a transformation of the Euclidean plane that maps circles or lines to other circles or lines and that preserves the angles between crossing curves. Many difficult problems in geometry become much more tractable when an inversion is applied. Inversion seems to have been discovered by a number of people contemporaneously, including Steiner (1824), Quetelet (1825), Bellavitis (1836), Stubbs and Ingram (1842–3) and Kelvin (1845).[1]
The concept of inversion can be generalized to higher-dimensional spaces.
Inversion in a circle
[edit]
Inverse of a point
[edit]
To invert a number in arithmetic usually means to take its reciprocal. A closely related idea in geometry is that of "inverting" a point. In the plane, the inverse of a point P with respect to a reference circle (Ø) with center O and radius r is a point P', lying on the ray from O through P such that
This is called circle inversion or plane inversion. The inversion taking any point P (other than O) to its image P' also takes P' back to P, so the result of applying the same inversion twice is the identity transformation which makes it a self-inversion (i.e. an involution).[2][3] To make the inversion a total function that is also defined for O, it is necessary to introduce a point at infinity, a single point placed on all the lines, and extend the inversion, by definition, to interchange the center O and this point at infinity.
It follows from the definition that the inversion of any point inside the reference circle must lie outside it, and vice versa, with the center and the point at infinity changing positions, whilst any point on the circle is unaffected (is invariant under inversion). In summary, for a point inside the circle, the nearer the point to the center, the further away its transformation. While for any point (inside or outside the circle), the nearer the point to the circle, the closer its transformation.
Compass and straightedge construction
[edit]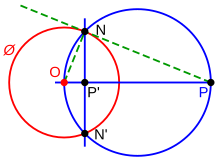
Point outside circle
[edit]To construct the inverse P' of a point P outside a circle Ø:
- Draw the segment from O (center of circle Ø) to P.
- Let M be the midpoint of OP. (Not shown)
- Draw the circle c with center M going through P. (Not labeled. It's the blue circle)
- Let N and N' be the points where Ø and c intersect.
- Draw segment NN'.
- P' is where OP and NN' intersect.
Point inside circle
[edit]To construct the inverse P of a point P' inside a circle Ø:
- Draw ray r from O (center of circle Ø) through P'. (Not labeled, it's the horizontal line)
- Draw line s through P' perpendicular to r. (Not labeled. It's the vertical line)
- Let N be one of the points where Ø and s intersect.
- Draw the segment ON.
- Draw line t through N perpendicular to ON.
- P is where ray r and line t intersect.
Dutta's construction
[edit]There is a construction of the inverse point to A with respect to a circle P that is independent of whether A is inside or outside P.[4]
Consider a circle P with center O and a point A which may lie inside or outside the circle P.
- Take the intersection point C of the ray OA with the circle P.
- Connect the point C with an arbitrary point B on the circle P (different from C and from the point on P antipodal to C)
- Let h be the reflection of ray BA in line BC. Then h cuts ray OC in a point A'. A' is the inverse point of A with respect to circle P.[4]: § 3.2
Properties
[edit]-
The inverse, with respect to the red circle, of a circle going through O (blue) is a line not going through O (green), and vice versa.
-
The inverse, with respect to the red circle, of a circle not going through O (blue) is a circle not going through O (green), and vice versa.
-
Inversion with respect to a circle does not map the center of the circle to the center of its image
The inversion of a set of points in the plane with respect to a circle is the set of inverses of these points. The following properties make circle inversion useful.
- A circle that passes through the center O of the reference circle inverts to a line not passing through O, but parallel to the tangent to the original circle at O, and vice versa; whereas a line passing through O is inverted into itself (but not pointwise invariant).[5]
- A circle not passing through O inverts to a circle not passing through O. If the circle meets the reference circle, these invariant points of intersection are also on the inverse circle. A circle (or line) is unchanged by inversion if and only if it is orthogonal to the reference circle at the points of intersection.[5]
Additional properties include:
- If a circle q passes through two distinct points A and A' which are inverses with respect to a circle k, then the circles k and q are orthogonal.
- If the circles k and q are orthogonal, then a straight line passing through the center O of k and intersecting q, does so at inverse points with respect to k.
- Given a triangle OAB in which O is the center of a circle k, and points A' and B' inverses of A and B with respect to k, then
- The points of intersection of two circles p and q orthogonal to a circle k, are inverses with respect to k.
- If M and M' are inverse points with respect to a circle k on two curves m and m', also inverses with respect to k, then the tangents to m and m' at the points M and M' are either perpendicular to the straight line MM' or form with this line an isosceles triangle with base MM'.
- Inversion leaves the measure of angles unaltered, but reverses the orientation of oriented angles.[6]
Examples in two dimensions
[edit]
- Inversion of a line is a circle containing the center of inversion; or it is the line itself if it contains the center
- Inversion of a circle is another circle; or it is a line if the original circle contains the center
- Inversion of a parabola is a cardioid
- Inversion of hyperbola is a lemniscate of Bernoulli
Application
[edit]For a circle not passing through the center of inversion, the center of the circle being inverted and the center of its image under inversion are collinear with the center of the reference circle. This fact can be used to prove that the Euler line of the intouch triangle of a triangle coincides with its OI line. The proof roughly goes as below:
Invert with respect to the incircle of triangle ABC. The medial triangle of the intouch triangle is inverted into triangle ABC, meaning the circumcenter of the medial triangle, that is, the nine-point center of the intouch triangle, the incenter and circumcenter of triangle ABC are collinear.
Any two non-intersecting circles may be inverted into concentric circles. Then the inversive distance (usually denoted δ) is defined as the natural logarithm of the ratio of the radii of the two concentric circles.
In addition, any two non-intersecting circles may be inverted into congruent circles, using circle of inversion centered at a point on the circle of antisimilitude.
The Peaucellier–Lipkin linkage is a mechanical implementation of inversion in a circle. It provides an exact solution to the important problem of converting between linear and circular motion.
Pole and polar
[edit]
If point R is the inverse of point P then the lines perpendicular to the line PR through one of the points is the polar of the other point (the pole).
Poles and polars have several useful properties:
- If a point P lies on a line l, then the pole L of the line l lies on the polar p of point P.
- If a point P moves along a line l, its polar p rotates about the pole L of the line l.
- If two tangent lines can be drawn from a pole to the circle, then its polar passes through both tangent points.
- If a point lies on the circle, its polar is the tangent through this point.
- If a point P lies on its own polar line, then P is on the circle.
- Each line has exactly one pole.
In three dimensions
[edit]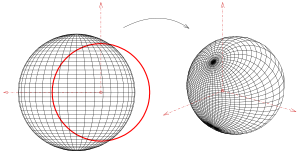


Circle inversion is generalizable to sphere inversion in three dimensions. The inversion of a point P in 3D with respect to a reference sphere centered at a point O with radius R is a point P ' on the ray with direction OP such that . As with the 2D version, a sphere inverts to a sphere, except that if a sphere passes through the center O of the reference sphere, then it inverts to a plane. Any plane passing through O, inverts to a sphere touching at O. A circle, that is, the intersection of a sphere with a secant plane, inverts into a circle, except that if the circle passes through O it inverts into a line. This reduces to the 2D case when the secant plane passes through O, but is a true 3D phenomenon if the secant plane does not pass through O.
Examples in three dimensions
[edit]Sphere
[edit]The simplest surface (besides a plane) is the sphere. The first picture shows a non trivial inversion (the center of the sphere is not the center of inversion) of a sphere together with two orthogonal intersecting pencils of circles.
Cylinder, cone, torus
[edit]The inversion of a cylinder, cone, or torus results in a Dupin cyclide.
Spheroid
[edit]A spheroid is a surface of revolution and contains a pencil of circles which is mapped onto a pencil of circles (see picture). The inverse image of a spheroid is a surface of degree 4.
Hyperboloid of one sheet
[edit]A hyperboloid of one sheet, which is a surface of revolution contains a pencil of circles which is mapped onto a pencil of circles. A hyperboloid of one sheet contains additional two pencils of lines, which are mapped onto pencils of circles. The picture shows one such line (blue) and its inversion.
Stereographic projection as the inversion of a sphere
[edit]
A stereographic projection usually projects a sphere from a point (north pole) of the sphere onto the tangent plane at the opposite point (south pole). This mapping can be performed by an inversion of the sphere onto its tangent plane. If the sphere (to be projected) has the equation (alternately written ; center , radius , green in the picture), then it will be mapped by the inversion at the unit sphere (red) onto the tangent plane at point . The lines through the center of inversion (point ) are mapped onto themselves. They are the projection lines of the stereographic projection.
6-sphere coordinates
[edit]The 6-sphere coordinates are a coordinate system for three-dimensional space obtained by inverting the Cartesian coordinates.
Axiomatics and generalization
[edit]One of the first to consider foundations of inversive geometry was Mario Pieri in 1911 and 1912.[7] Edward Kasner wrote his thesis on "Invariant theory of the inversion group".[8]
More recently the mathematical structure of inversive geometry has been interpreted as an incidence structure where the generalized circles are called "blocks": In incidence geometry, any affine plane together with a single point at infinity forms a Möbius plane, also known as an inversive plane. The point at infinity is added to all the lines. These Möbius planes can be described axiomatically and exist in both finite and infinite versions.
A model for the Möbius plane that comes from the Euclidean plane is the Riemann sphere.
Invariant
[edit]The cross-ratio between 4 points is invariant under an inversion. In particular if O is the centre of the inversion and and are distances to the ends of a line L, then length of the line will become under an inversion with radius 1. The invariant is:
Relation to Erlangen program
[edit]According to Coxeter,[9] the transformation by inversion in circle was invented by L. I. Magnus in 1831. Since then this mapping has become an avenue to higher mathematics. Through some steps of application of the circle inversion map, a student of transformation geometry soon appreciates the significance of Felix Klein's Erlangen program, an outgrowth of certain models of hyperbolic geometry
Dilation
[edit]The combination of two inversions in concentric circles results in a similarity, homothetic transformation, or dilation characterized by the ratio of the circle radii.
Reciprocation
[edit]When a point in the plane is interpreted as a complex number with complex conjugate then the reciprocal of z is
Consequently, the algebraic form of the inversion in a unit circle is given by where:
- .
Reciprocation is key in transformation theory as a generator of the Möbius group. The other generators are translation and rotation, both familiar through physical manipulations in the ambient 3-space. Introduction of reciprocation (dependent upon circle inversion) is what produces the peculiar nature of Möbius geometry, which is sometimes identified with inversive geometry (of the Euclidean plane). However, inversive geometry is the larger study since it includes the raw inversion in a circle (not yet made, with conjugation, into reciprocation). Inversive geometry also includes the conjugation mapping. Neither conjugation nor inversion-in-a-circle are in the Möbius group since they are non-conformal (see below). Möbius group elements are analytic functions of the whole plane and so are necessarily conformal.
Transforming circles into circles
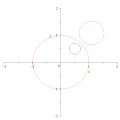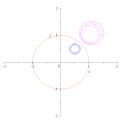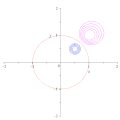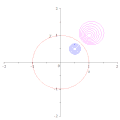
[edit]Consider, in the complex plane, the circle of radius around the point
where without loss of generality, Using the definition of inversion
it is straightforward to show that obeys the equation
and hence that describes the circle of center and radius
When the circle transforms into the line parallel to the imaginary axis
For and the result for is
showing that the describes the circle of center and radius .
When the equation for becomes
Higher geometry
[edit]As mentioned above, zero, the origin, requires special consideration in the circle inversion mapping. The approach is to adjoin a point at infinity designated ∞ or 1/0 . In the complex number approach, where reciprocation is the apparent operation, this procedure leads to the complex projective line, often called the Riemann sphere. It was subspaces and subgroups of this space and group of mappings that were applied to produce early models of hyperbolic geometry by Beltrami, Cayley, and Klein. Thus inversive geometry includes the ideas originated by Lobachevsky and Bolyai in their plane geometry. Furthermore, Felix Klein was so overcome by this facility of mappings to identify geometrical phenomena that he delivered a manifesto, the Erlangen program, in 1872. Since then many mathematicians reserve the term geometry for a space together with a group of mappings of that space. The significant properties of figures in the geometry are those that are invariant under this group.
For example, Smogorzhevsky[10] develops several theorems of inversive geometry before beginning Lobachevskian geometry.
In higher dimensions
[edit]In a real n-dimensional Euclidean space, an inversion in the sphere of radius r centered at the point is a map of an arbitrary point found by inverting the length of the displacement vector and multiplying by :
The transformation by inversion in hyperplanes or hyperspheres in En can be used to generate dilations, translations, or rotations. Indeed, two concentric hyperspheres, used to produce successive inversions, result in a dilation or homothety about the hyperspheres' center.
When two parallel hyperplanes are used to produce successive reflections, the result is a translation. When two hyperplanes intersect in an (n–2)-flat, successive reflections produce a rotation where every point of the (n–2)-flat is a fixed point of each reflection and thus of the composition.
Any combination of reflections, translations, and rotations is called an isometry. Any combination of reflections, dilations, translations, and rotations is a similarity.
All of these are conformal maps, and in fact, where the space has three or more dimensions, the mappings generated by inversion are the only conformal mappings. Liouville's theorem is a classical theorem of conformal geometry.
The addition of a point at infinity to the space obviates the distinction between hyperplane and hypersphere; higher dimensional inversive geometry is frequently studied then in the presumed context of an n-sphere as the base space. The transformations of inversive geometry are often referred to as Möbius transformations. Inversive geometry has been applied to the study of colorings, or partitionings, of an n-sphere.[11]
Anticonformal mapping property
[edit]The circle inversion map is anticonformal, which means that at every point it preserves angles and reverses orientation (a map is called conformal if it preserves oriented angles). Algebraically, a map is anticonformal if at every point the Jacobian is a scalar times an orthogonal matrix with negative determinant: in two dimensions the Jacobian must be a scalar times a reflection at every point. This means that if J is the Jacobian, then and Computing the Jacobian in the case zi = xi/‖x‖2, where ‖x‖2 = x12 + ... + xn2 gives JJT = kI, with k = 1/‖x‖4n, and additionally det(J) is negative; hence the inversive map is anticonformal.
In the complex plane, the most obvious circle inversion map (i.e., using the unit circle centered at the origin) is the complex conjugate of the complex inverse map taking z to 1/z. The complex analytic inverse map is conformal and its conjugate, circle inversion, is anticonformal. In this case a homography is conformal while an anti-homography is anticonformal.
Inversive geometry and hyperbolic geometry
[edit]The (n − 1)-sphere with equation
will have a positive radius if a12 + ... + an2 is greater than c, and on inversion gives the sphere
Hence, it will be invariant under inversion if and only if c = 1. But this is the condition of being orthogonal to the unit sphere. Hence we are led to consider the (n − 1)-spheres with equation
which are invariant under inversion, orthogonal to the unit sphere, and have centers outside of the sphere. These together with the subspace hyperplanes separating hemispheres are the hypersurfaces of the Poincaré disc model of hyperbolic geometry.
Since inversion in the unit sphere leaves the spheres orthogonal to it invariant, the inversion maps the points inside the unit sphere to the outside and vice versa. This is therefore true in general of orthogonal spheres, and in particular inversion in one of the spheres orthogonal to the unit sphere maps the unit sphere to itself. It also maps the interior of the unit sphere to itself, with points outside the orthogonal sphere mapping inside, and vice versa; this defines the reflections of the Poincaré disc model if we also include with them the reflections through the diameters separating hemispheres of the unit sphere. These reflections generate the group of isometries of the model, which tells us that the isometries are conformal. Hence, the angle between two curves in the model is the same as the angle between two curves in the hyperbolic space.
See also
[edit]- Circle of antisimilitude
- Duality (projective geometry)
- Inverse curve
- Limiting point (geometry)
- Möbius transformation
- Projective geometry
- Soddy's hexlet
- Mohr-Mascheroni theorem
- Inversion of curves and surfaces (German)
Notes
[edit]- ^ Curves and Their Properties by Robert C. Yates, National Council of Teachers of Mathematics, Inc., Washington, D.C., p. 127: "Geometrical inversion seems to be due to Jakob Steiner who indicated a knowledge of the subject in 1824. He was closely followed by Adolphe Quetelet (1825) who gave some examples. Apparently independently discovered by Giusto Bellavitis in 1836, by Stubbs and Ingram in 1842–3, and by Lord Kelvin in 1845.)"
- ^ Altshiller-Court (1952, p. 230)
- ^ Kay (1969, p. 264)
- ^ a b Dutta, Surajit (2014) A simple property of isosceles triangles with applications Archived 2018-04-21 at the Wayback Machine, Forum Geometricorum 14: 237–240
- ^ a b Kay (1969, p. 265)
- ^ Kay (1969, p. 269)
- ^ M. Pieri (1911,12) "Nuovi principia di geometria della inversion", Giornal di Matematiche di Battaglini 49:49–96 & 50:106–140
- ^ Kasner, E. (1900). "The Invariant Theory of the Inversion Group: Geometry Upon a Quadric Surface". Transactions of the American Mathematical Society. 1 (4): 430–498. doi:10.1090/S0002-9947-1900-1500550-1. hdl:2027/miun.abv0510.0001.001. JSTOR 1986367.
- ^ Coxeter 1969, pp. 77–95
- ^ A.S. Smogorzhevsky (1982) Lobachevskian Geometry, Mir Publishers, Moscow
- ^ Joel C. Gibbons & Yushen Luo (2013) Colorings of the n-sphere and inversive geometry
References
[edit]- Altshiller-Court, Nathan (1952), College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle (2nd ed.), New York: Barnes & Noble, LCCN 52-13504
- Blair, David E. (2000), Inversion Theory and Conformal Mapping, American Mathematical Society, ISBN 0-8218-2636-0
- Brannan, David A.; Esplen, Matthew F.; Gray, Jeremy J. (1998), "Chapter 5: Inversive Geometry", Geometry, Cambridge: Cambridge University Press, pp. 199–260, ISBN 0-521-59787-0
- Coxeter, H.S.M. (1969) [1961], Introduction to Geometry (2nd ed.), John Wiley & Sons, ISBN 0-471-18283-4
- Hartshorne, Robin (2000), "Chapter 7: Non-Euclidean Geometry, Section 37: Circular Inversion", Geometry: Euclid and Beyond, Springer, ISBN 0-387-98650-2
- Kay, David C. (1969), College Geometry, New York: Holt, Rinehart and Winston, LCCN 69-12075
- Patterson, Boyd (1941) "The Inversive Plane", American Mathematical Monthly 48: 589–99, doi:10.2307/2303867 MR0006034
External links
[edit]- Inversion: Reflection in a Circle at cut-the-knot
- Wilson Stother's inversive geometry page
- IMO Compendium Training Materials practice problems on how to use inversion for math olympiad problems
- Weisstein, Eric W. "Inversion". MathWorld.
- Visual Dictionary of Special Plane Curves Xah Lee





































![{\displaystyle {\begin{aligned}&ww^{*}-{\frac {aw+a^{*}w^{*}}{(a^{*}a-r^{2})}}+{\frac {aa^{*}}{(aa^{*}-r^{2})^{2}}}={\frac {r^{2}}{(aa^{*}-r^{2})^{2}}}\\[4pt]\Longleftrightarrow {}&\left(w-{\frac {a^{*}}{aa^{*}-r^{2}}}\right)\left(w^{*}-{\frac {a}{a^{*}a-r^{2}}}\right)=\left({\frac {r}{\left|aa^{*}-r^{2}\right|}}\right)^{2}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9aa6efc01b1fd1b842804099c2595fcb27ea2ee0)



![{\displaystyle {\begin{aligned}&aw+a^{*}w^{*}=1\Longleftrightarrow 2\operatorname {Re} \{aw\}=1\Longleftrightarrow \operatorname {Re} \{a\}\operatorname {Re} \{w\}-\operatorname {Im} \{a\}\operatorname {Im} \{w\}={\frac {1}{2}}\\[4pt]\Longleftrightarrow {}&\operatorname {Im} \{w\}={\frac {\operatorname {Re} \{a\}}{\operatorname {Im} \{a\}}}\cdot \operatorname {Re} \{w\}-{\frac {1}{2\cdot \operatorname {Im} \{a\}}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b252d9984bc3b1ce123df34bd78d93f6c3accef)




![{\displaystyle {\begin{aligned}P&\mapsto P'=O+{\frac {r^{2}(P-O)}{\|P-O\|^{2}}},\\[5mu]p_{j}&\mapsto p_{j}'=o_{j}+{\frac {r^{2}(p_{j}-o_{j})}{\sum _{k}(p_{k}-o_{k})^{2}}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8d3570ef2a3e7bb3c4daedbf92471160fff616d)




