Knight's tour

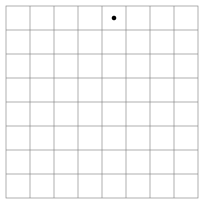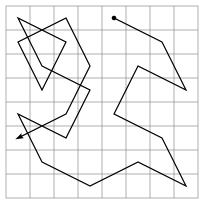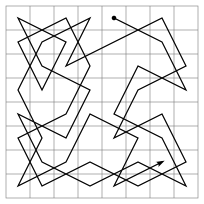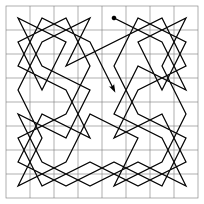
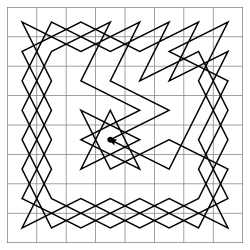
The Knight's Tour is a mathematical problem involving a knight on a chessboard. The knight is placed on the empty board and, moving according to the rules of chess, must visit each square exactly once.

There are a great many solutions to the problem, of which exactly 26,534,728,821,064 have the knight finishing on a square from which it attacks the starting square, on an 8x8 board. ^[1] Such a tour is described as directed and closed. (A directed tour is a directed graph: the direction of the tour is specified. A closed tour is one that ends on the starting square.) The number of undirected closed tours is half this number, since every tour can be traced in reverse. Otherwise the tour is open (as in the first diagram). There are 9,862 undirected closed tours on a 6x6 board, and no such tours on smaller boards ^[2].

Many variations on this topic have been studied by mathematicians, including Euler, over the centuries using:

differently sized boards
two-player games based on this idea
problems using slight variations on the way the knight moves.

The knight's tour problem is an instance of the more general Hamiltonian path problem in graph theory, which is NP-complete. The problem of getting a closed knight's tour is similarly an instance of the hamiltonian cycle problem. Note however that, unlike the general Hamiltonian path problem, the knight's tour problem can be solved in linear time.^[3]

The pattern of a Knight's Tour on a half-board has been presented in verse form (as a literary constraint) in the highly stylized Sanskrit poem Kavyalankara^[4] written by the 9th century Kashmiri poet Rudrata, which discusses the art of poetry, especially with relation to theater (Natyashastra). As was often the practice in ornate Sanskrit poetry, the syllabic patterns of this poem elucidate a completely different motif, in this case an open knight's tour on a half-chessboard.

The first algorithm for completing the Knight's Tour was Warnsdorff's algorithm, first described in 1823 by H. C. Warnsdorff.

In the 20th century the Oulipo group of writers used it among many others. The most notable example is the 10 × 10 Knight's Tour which sets the order of the chapters in Georges Perec's novel Life: A User's Manual.

Schwenk's Theorem

For any m × n board with m less than or equal to n, a closed knight's tour is always possible unless one or more of these three conditions are true:

m and n are both odd
m = 1, 2, or 4; m and n are not both 1
m = 3 and n = 4, 6, or 8

Condition 1

It is not hard to show that when condition 1 is true a closed knight's tour is impossible.

Imagine a chessboard colored black and white in the manner that we are all familiar with (alternating). Whenever a knight moves it lands on the opposite color. If it is on white, it moves to black. If it is on black, it moves to white.

Since m and n are both odd, the number of white squares and black squares are different. For example, in a 5×5 checkerboard there are 13 of one color and 12 of the other.

For a knight to have a closed tour it must visit the same number of white squares and black squares. But we have just seen that odd × odd boards have a different number of white squares and black squares, therefore closed tours do not exist. Open tours may still exist.

Condition 2

Condition 2 states that when the shorter side is length 1, 2, or 4, no closed tour is possible.

It is easy to see why when m = 1 or 2 that no knight's tour is possible: the knight would not be able to reach every square (with the exception of the trivial case 1x1).

It can be shown that a 4 × n board cannot have a closed tour.

Start by assuming that a 4 × n board has a closed knight's tour. Let us construct 2 sets of squares, $A_{1}$ and $B_{1}$ , $A_{1}$ containing one half of the squares on the board and $B_{1}$ containing the other half of the squares on the board. If we color this 4 × n board with a checkerboard pattern, we can define $A_{1}$ as the set of white squares and $B_{1}$ as the set of black squares. As previously established, the knight must alternate between white and black ( $A_{1}$ and $B_{1}$ ).

The knight must alternate between green and red.

Consider the figure on the right. Define $A_{2}$ as the set of green squares and $B_{2}$ as the set of red squares in the figure. There are an equal number of red squares as green squares. Note that from a square in $A_{2}$ the knight must next jump to a square in $B_{2}$ . And since the knight must visit every square, when the knight is on a $B_{2}$ square in must move to an $A_{2}$ next (otherwise the knight will need to make a repeat on an $A_{2}$ square as well, but this is impossible).

If we follow the knight we will find a contradiction.

The first square the knight goes to will be a square of $A_{1}$ and $A_{2}$ . If it is not, we switch $A_{2}$ and $B_{2}$ so that it is true.
The second square must be an element of the sets $B_{1}$ and $B_{2}$ .
The third square must be an element of $A_{1}$ and $A_{2}$ .
The fourth square must be an element of the sets $B_{1}$ and $B_{2}$ .
And so on.

It follows that set $A_{1}$ has the same elements as set $A_{2}$ , and set $B_{1}$ has the same elements as set $B_{2}$ . But this is obviously not true, as the red and green pattern shown above is not the same as a checkerboard pattern; the set of red squares is not the same as the set of black squares (or white, for that matter).

So our above assumption was false and there are no closed knight's tours for and 4 × n board, for any n.

Condition 3

Condition 3 is proved case by case. Attempting to construct a closed knight's tour on a 3 by 4, 3 by 6, or 3 by 8 will lead to definite failure.

3 by n boards with n not equal to 4, 6, or 8 can be shown to be possible with a repeated pattern.

All other cases

Simply proving the above three conditions does not prove the theorem; it is still required to prove that all rectangular boards that do not fall in one of the above three categories have knight's tours.

References

^ Wegener, I. (January 1, 1987). Branching Programs and Binary Decision Diagrams. Society for Industrial & Applied Mathematics. ISBN 0-898-71458-3.
^ http://mathworld.wolfram.com/KnightsTour.html
^ A. Conrad, T. Hindrichs, H. Morsy, and I. Wegener. "Solution of the Knight's Hamiltonian Path Problem on Chessboards." Discrete Applied Math, volume 50, no.2, pp.125-134. 1994.
^ Satyadev, Chaudhary. Kavyalankara of Rudrata (Sanskrit Text, with Hindi translation);. Delhi: Parimal Sanskrit Series No. 30.

Watkins, John J. Across the Board: the Mathematics of Chessboard Problems. Princeton UP, 2004.

External links

[1] Wegener, I. (January 1, 1987). Branching Programs and Binary Decision Diagrams. Society for Industrial & Applied Mathematics. ISBN 0-898-71458-3.

[2] ttp://mathworld.wolfram.com/KnightsTour.html

[3] A. Conrad, T. Hindrichs, H. Morsy, and I. Wegener. "Solution of the Knight's Hamiltonian Path Problem on Chessboards." Discrete Applied Math, volume 50, no.2, pp.125-134. 1994.

[4] Satyadev, Chaudhary. Kavyalankara of Rudrata (Sanskrit Text, with Hindi translation);. Delhi: Parimal Sanskrit Series No. 30.

[1]

[2]

[3]

[4]