Kuramoto–Sivashinsky equation

In mathematics, the Kuramoto–Sivashinsky equation (also called the KS equation or flame equation) is a fourth-order nonlinear partial differential equation. It is named after Yoshiki Kuramoto and Gregory Sivashinsky, who derived the equation in the late 1970s to model the diffusive–thermal instabilities in a laminar flame front.[1][2][3] The Kuramoto–Sivashinsky equation is known for its chaotic behavior.[4][5]
Definition
The 1d version of the Kuramoto–Sivashinsky equation is
An alternate form is
obtained by differentiating with respect to and substituting . This is the form used in fluid dynamics applications.[6]
The Kuramoto–Sivashinsky equation can also be generalized to higher dimensions. In spatially periodic domains, one possibility is
where is the Laplace operator, and is the biharmonic operator.
Properties
The Cauchy problem for the 1d Kuramoto–Sivashinsky equation is well-posed in the sense of Hadamard—that is, for given initial data , there exists a unique solution that depends continuously on the initial data.[7]
The 1d Kuramoto–Sivashinsky equation possesses Galilean invariance—that is, if is a solution, then so is , where is an arbitrary constant.[8] Physically, since is a velocity, this change of variable describes a transformation into a frame that is moving with constant relative velocity . On a periodic domain, the equation also has a reflection symmetry: if is a solution, then is also a solution.[8]
Solutions
Solutions of the Kuramoto–Sivashinsky equation possess rich dynamical characteristics.[8][9][10] Considered on a periodic domain , the dynamics undergoes a series of bifurcations as the domain size is increased, culminating in the onset of chaotic behavior. Depending on the value of , solutions may include equilibria, relative equilibria, and traveling waves—all of which typically become dynamically unstable as is increased. In particular, the transition to chaos occurs by a cascade of period-doubling bifurcations.[10]
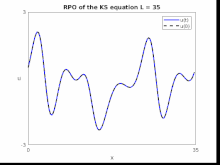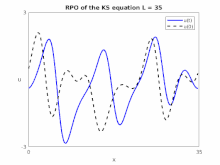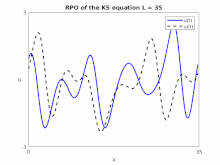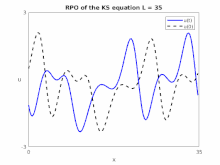
Applications
Applications of the Kuramoto–Sivashinsky equation extend beyond its original context of flame propagation and reaction–diffusion systems. These additional applications include flows in pipes and at interfaces, plasmas, chemical reaction dynamics, and models of ion-sputtered surfaces.[6][11]
See also
- List of nonlinear partial differential equations
- List of chaotic maps
- Clarke's equation
- Laminar flame speed
References
- ^ Kuramoto, Yoshiki (1978). "Diffusion-Induced Chaos in Reaction Systems". Progress of Theoretical Physics Supplement. 64: 346–367. doi:10.1143/PTPS.64.346. ISSN 0375-9687.
- ^ Sivashinsky, G.I. (1977). "Nonlinear analysis of hydrodynamic instability in laminar flames—I. Derivation of basic equations". Acta Astronautica. 4 (11–12): 1177–1206. doi:10.1016/0094-5765(77)90096-0. ISSN 0094-5765.
- ^ Sivashinsky, G. I. (1980). "On Flame Propagation Under Conditions of Stoichiometry". SIAM Journal on Applied Mathematics. 39 (1): 67–82. doi:10.1137/0139007. ISSN 0036-1399.
- ^ Pathak, Jaideep; Hunt, Brian; Girvan, Michelle; Lu, Zhixin; Ott, Edward (2018). "Model-Free Prediction of Large Spatiotemporally Chaotic Systems from Data: A Reservoir Computing Approach". Physical Review Letters. 120 (2): 024102. doi:10.1103/PhysRevLett.120.024102. ISSN 0031-9007. PMID 29376715.
- ^ Vlachas, P.R.; Pathak, J.; Hunt, B.R.; Sapsis, T.P.; Girvan, M.; Ott, E.; Koumoutsakos, P. (2020-03-21). "Backpropagation algorithms and Reservoir Computing in Recurrent Neural Networks for the forecasting of complex spatiotemporal dynamics". Neural Networks. 126: 191–217. doi:10.1016/j.neunet.2020.02.016. ISSN 0893-6080. PMID 32248008. S2CID 211146609.
- ^ a b Kalogirou, A.; Keaveny, E. E.; Papageorgiou, D. T. (2015). "An in-depth numerical study of the two-dimensional Kuramoto–Sivashinsky equation". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 471 (2179): 20140932. doi:10.1098/rspa.2014.0932. ISSN 1364-5021. PMC 4528647. PMID 26345218.
- ^ Tadmor, Eitan (1986). "The Well-Posedness of the Kuramoto–Sivashinsky Equation". SIAM Journal on Mathematical Analysis. 17 (4): 884–893. doi:10.1137/0517063. hdl:1903/8432. ISSN 0036-1410.
- ^ a b c Cvitanović, Predrag; Davidchack, Ruslan L.; Siminos, Evangelos (2010). "On the State Space Geometry of the Kuramoto–Sivashinsky Flow in a Periodic Domain". SIAM Journal on Applied Dynamical Systems. 9 (1): 1–33. arXiv:0709.2944. doi:10.1137/070705623. ISSN 1536-0040. S2CID 17048798.
- ^ Michelson, Daniel (1986). "Steady solutions of the Kuramoto-Sivashinsky equation". Physica D: Nonlinear Phenomena. 19 (1): 89–111. doi:10.1016/0167-2789(86)90055-2. ISSN 0167-2789.
- ^ a b Papageorgiou, D.T.; Smyrlis, Y.S. (1991), "The route to chaos for the Kuramoto-Sivashinsky equation", Theoret. Comput. Fluid Dynamics, 3: 15–42, doi:10.1007/BF00271514, hdl:2060/19910004329, ISSN 1432-2250, S2CID 116955014
- ^ Cuerno, Rodolfo; Barabási, Albert-László (1995). "Dynamic Scaling of Ion-Sputtered Surfaces". Physical Review Letters. 74 (23): 4746–4749. arXiv:cond-mat/9411083. doi:10.1103/PhysRevLett.74.4746. ISSN 0031-9007. PMID 10058588. S2CID 18148655.

















