Minor chord
| Component intervals from root | |
|---|---|
| perfect fifth | |
| minor third | |
| root | |
| Tuning | |
| 10:12:15[1] | |
| Forte no. / | |
| 3-11 / |
In music theory, a minor chord is a chord that has a root, a minor third, and a perfect fifth.[2] When a chord comprises only these three notes, it is called a minor triad. For example, the minor triad built on A, called an A minor triad, has pitches A–C-E:
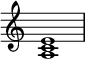

In harmonic analysis and on lead sheets, a C minor chord can be notated as Cm, C−, Cmin, or simply the lowercase "c". A minor triad is represented by the integer notation {0, 3, 7}.
A minor triad can also be described by its intervals: the interval between the bottom and middle notes is a minor third, and the interval between the middle and top notes is a major third. By contrast, a major triad has a major third on the bottom and minor third on top. They both contain fifths, because a minor third (three semitones) plus a major third (four semitones) equals a perfect fifth (seven semitones). Chords that are constructed of consecutive (or "stacked") thirds are called tertian.
In Western classical music from 1600 to 1820 and in Western pop, folk and rock music, a major chord is usually played as a triad. Along with the major triad, the minor triad is one of the basic building blocks of tonal music and the common practice period. In Western music, a minor chord, in comparison, "sounds darker than a major chord"[3] but is still considered highly consonant, stable, or as not requiring resolution.
Some minor chords with additional notes, such as the minor seventh chord, may also be called minor chords.
Acoustic consonance of the minor chord[edit]
A unique particularity of the minor chord is that this is the only chord of three notes in which the three notes have one harmonic – hearable and with a not too high row – in common (more or less exactly, depending on the tuning system used). This harmonic, common to the three notes, is situated 2 octaves above the high note of the chord. This is the sixth harmonic of the root of the chord, the fifth of the middle note, and the fourth of the high note:
- In the example C, E♭, G, the common harmonic is a G 2 octaves above.
Demonstration:
- Minor third = 6:5 = 12:10
- Major third = 5:4 = 15:12
- So the ratios of minor chord are 10:12:15
- And the explication of the unique harmonic in common, between the three notes, is verified by : 10 × 6 = 12 × 5 = 15 × 4
Just intonation[edit]

In just intonation, a minor chord is often (but not exclusively) tuned in the frequency ratio 10:12:15 (ⓘ).[4] This is the first occurrence of a minor triad in the harmonic series (if on C: E–G–B).[5] This may be found on iii, vi, ♭vi, ♭iii, and vii.[6]
In 12-TET, or twelve-tone equal temperament (now the most common tuning system in the West), a minor chord has 3 semitones between the root and third, 4 between the third and fifth, and 7 between the root and fifth. It is represented by the integer notation 0,3,7. The 12-TET fifth (700 cents) is only two cents narrower than the just perfect fifth (3:2, 701.9 cents), but the 12-TET minor third (300 cents) is noticeably (about 16 cents) narrower than the just minor third (6:5, 315.6 cents). The 12-TET minor third (300 cents) more closely approximates the 19-limit (Limit (music)) minor third 16:19 ⓘ (297.5 cents, the nineteenth harmonic) with only 2 cents error.[7]
Ellis proposes that the conflict between mathematicians and physicists on one hand and practicing musicians on the other regarding the supposed inferiority of the minor chord and scale to the major may be explained due to physicists' comparison of just minor and major triads, in which case minor comes out the loser, versus the musicians' comparison of the equal tempered triads, in which case minor comes out the winner since the ET major third is 14 cents sharp from the just major third while the ET minor third closely approximates the consonant 19:16 minor third, which many find pleasing.[8][full citation needed]
In the 16th through 18th centuries, prior to 12-TET, the minor third in meantone temperament was 310 cents ⓘ and much rougher than the 300 cent ET minor third. Other just minor chord tunings include the supertonic triad in just intonation (27:32:40)[4] the false minor triad,[9] ⓘ, 16:19:24[10] ⓘ, 12:14:18 (6:7:9)[11][12] ⓘ (septimal minor third), and the Pythagorean minor triad[10] (54:64:81) ⓘ. More tunings of the minor chord are also available in various equal temperaments other than 12-TET.
Rather than directly from the harmonic series, Sorge derived the minor chord from joining two major triads; for example the A minor triad being the confluence of the F and C major triads.[13] A–C–E = F–A–C–E–G. Given justly tuned major triads this produces a justly tuned minor triad: 10:12:15 on 8:5.
Minor chord table[edit]
See also[edit]
References[edit]
- ^ Shirlaw, Matthew (16 June 2015). The Theory of Harmony. p. 81. ISBN 978-1-4510-1534-8.
20:24:30
- ^ Miller, Michael (2005). The Complete Idiot's Guide to Music Theory (2nd ed.). Indianapolis: Alpha. p. 114. ISBN 1-59257-437-8.
- ^ Kamien, Roger (2008). Music: An Appreciation (6th brief ed.). p. 46. ISBN 978-0-07-340134-8.
- ^ a b Johnston, Ben; Gilmore, Bob (2006) [2003]. "A Notation System for Extended Just Intonation". "Maximum Clarity" and Other Writings on Music. p. 78. ISBN 978-0-252-03098-7.
D−, F, A (10/9–4/3–5/3)
- ^ Hauptmann, Moritz (1888). The Nature of Harmony and Metre. Swan Sonnenschein. p. 15.
- ^ Wright, David (2009). Mathematics and Music. pp. 140–141. ISBN 978-0-8218-4873-9.
- ^ Helmholtz, Hermann (1954). On the Sensations of Tone as a Physiological Basis for the Theory of Music. Translated by Ellis, Alexander J. New York: Dover Publications. p. 455.
- ^ Ellis (1954), p.298.
- ^ Shirlaw, Matthew (16 June 2015). The Theory of Harmony. p. 375. ISBN 978-1-4510-1534-8.
- ^ a b Ruland, Heiner (1992). Expanding Tonal Awareness. p. 39. ISBN 978-1-85584-170-3.
- ^ Helmholtz, Hermann (1885). On the Sensations of Tone as a Physiological Basis for the Theory of Music. Longmans, Green. p. 468.
- ^ Mathews, William Smythe Babcock (1805). Music: A Monthly Magazine Devoted to the Art, Science, Technic and Literature of Music. 7: 608.
The tones re, fa, and la, as given on the accordion, are vibrationally 6:7:9. This is not a minor triad, nor anything very near it although its fifth is just the same as in the minor and the major, and the ratio 6:9 being simply 2:3.
{{cite journal}}: Missing or empty|title=(help) - ^ Lester, Joel (1994). Compositional Theory in the Eighteenth Century. p. 194. ISBN 978-0-674-15523-7.

