Optimal asymmetric encryption padding
In cryptography, Optimal Asymmetric Encryption Padding (OAEP) is a padding scheme often used together with RSA encryption. OAEP was introduced by Bellare and Rogaway,[1] and subsequently standardized in PKCS#1 v2 and RFC 2437.
The OAEP algorithm is a form of Feistel network which uses a pair of random oracles G and H to process the plaintext prior to asymmetric encryption. When combined with any secure trapdoor one-way permutation , this processing is proved in the random oracle model to result in a combined scheme which is semantically secure under chosen plaintext attack (IND-CPA). When implemented with certain trapdoor permutations (e.g., RSA), OAEP is also proven to be secure against chosen ciphertext attack. OAEP can be used to build an all-or-nothing transform.
OAEP satisfies the following two goals:
- Add an element of randomness which can be used to convert a deterministic encryption scheme (e.g., traditional RSA) into a probabilistic scheme.
- Prevent partial decryption of ciphertexts (or other information leakage) by ensuring that an adversary cannot recover any portion of the plaintext without being able to invert the trapdoor one-way permutation .
The original version of OAEP (Bellare/Rogaway, 1994) showed a form of "plaintext awareness" (which they claimed implies security against chosen ciphertext attack) in the random oracle model when OAEP is used with any trapdoor permutation. Subsequent results contradicted this claim, showing that OAEP was only IND-CCA1 secure. However, the original scheme was proved in the random oracle model to be IND-CCA2 secure when OAEP is used with the RSA permutation using standard encryption exponents, as in the case of RSA-OAEP.[2] An improved scheme (called OAEP+) that works with any trapdoor one-way permutation was offered by Victor Shoup to solve this problem.[3] More recent work has shown that in the standard model (that is, when hash functions are not modeled as random oracles) it is impossible to prove the IND-CCA2 security of RSA-OAEP under the assumed hardness of the RSA problem.[4][5]
Algorithm
[edit]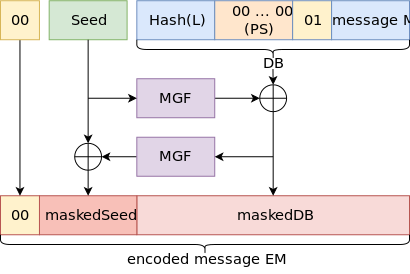
In the diagram,
- MGF is the mask generating function, usually MGF1,
- Hash is the chosen hash function,
- hLen is the length of the output of the hash function in bytes,
- k is the length of the RSA modulus n in bytes,
- M is the message to be padded, with length mLen (at most bytes),
- L is an optional label to be associated with the message (the label is the empty string by default and can be used to authenticate data without requiring encryption),
- PS is a byte string of null-bytes.
- ⊕ is an XOR-Operation.
Encoding
[edit]RFC 8017[6] for PKCS#1 v2.2 specifies the OAEP scheme as follows for encoding:
- Hash the label L using the chosen hash function:
- Generate a padding string PS consisting of bytes with the value 0x00.
- Concatenate lHash, PS, the single byte 0x01, and the message M to form a data block DB: . This data block has length bytes.
- Generate a random seed of length hLen.
- Use the mask generating function to generate a mask of the appropriate length for the data block:
- Mask the data block with the generated mask:
- Use the mask generating function to generate a mask of length hLen for the seed:
- Mask the seed with the generated mask:
- The encoded (padded) message is the byte 0x00 concatenated with the maskedSeed and maskedDB:
Decoding
[edit]Decoding works by reversing the steps taken in the encoding algorithm:
- Hash the label L using the chosen hash function:
- To reverse step 9, split the encoded message EM into the byte 0x00, the maskedSeed (with length hLen) and the maskedDB:
- Generate the seedMask which was used to mask the seed:
- To reverse step 8, recover the seed with the seedMask:
- Generate the dbMask which was used to mask the data block:
- To reverse step 6, recover the data block DB:
- To reverse step 3, split the data block into its parts: .
- Verify that:
- lHash' is equal to the computed lHash
- PS only consists of bytes 0x00
- PS and M are separated by the 0x01 byte and
- the first byte of EM is the byte 0x00.
- If any of these conditions aren't met, then the padding is invalid.
- Verify that:
Usage in RSA: The encoded message can then be encrypted with RSA. The deterministic property of RSA is now avoided by using the OAEP encoding because the seed is randomly generated and influences the entire encoded message.
Security
[edit]The "all-or-nothing" security is from the fact that to recover M, one must recover the entire maskedDB and the entire maskedSeed; maskedDB is required to recover the seed from the maskedSeed, and the seed is required to recover the data block DB from maskedDB. Since any changed bit of a cryptographic hash completely changes the result, the entire maskedDB, and the entire maskedSeed must both be completely recovered.
Implementation
[edit]In the PKCS#1 standard, the random oracles are identical. The PKCS#1 standard further requires that the random oracles be MGF1 with an appropriate hash function.[7]
See also
[edit]References
[edit]- ^ M. Bellare, P. Rogaway. Optimal Asymmetric Encryption -- How to encrypt with RSA. Extended abstract in Advances in Cryptology – Eurocrypt '94 Proceedings, Lecture Notes in Computer Science Vol. 950, A. De Santis ed, Springer-Verlag, 1995. full version (pdf)
- ^ Eiichiro Fujisaki, Tatsuaki Okamoto, David Pointcheval, and Jacques Stern. RSA-- OAEP is secure under the RSA assumption. In J. Kilian, ed., Advances in Cryptology – CRYPTO 2001, vol. 2139 of Lecture Notes in Computer Science, SpringerVerlag, 2001. full version (pdf)
- ^ Victor Shoup. OAEP Reconsidered. IBM Zurich Research Lab, Saumerstr. 4, 8803 Ruschlikon, Switzerland. September 18, 2001. full version (pdf)
- ^ P. Paillier and J. Villar, Trading One-Wayness against Chosen-Ciphertext Security in Factoring-Based Encryption, Advances in Cryptology – Asiacrypt 2006.
- ^ D. Brown, What Hashes Make RSA-OAEP Secure?, IACR ePrint 2006/233.
- ^ "Encryption Operation". PKCS #1: RSA Cryptography Specifications Version 2.2. IETF. November 2016. p. 22. sec. 7.1.1. doi:10.17487/RFC8017. RFC 8017. Retrieved 2022-06-04.
- ^ Brown, Daniel R. L. (2006). "What Hashes Make RSA-OAEP Secure?" (PDF). IACR Cryptology ePrint Archive. Retrieved 2019-04-03.














