Orthorhombic crystal system
In crystallography, the orthorhombic crystal system is one of the 7 crystal systems. Orthorhombic lattices result from stretching a cubic lattice along two of its orthogonal pairs by two different factors, resulting in a rectangular prism with a rectangular base (a by b) and height (c), such that a, b, and c are distinct. All three bases intersect at 90° angles, so the three lattice vectors remain mutually orthogonal.
Bravais lattices
[edit]There are four orthorhombic Bravais lattices: primitive orthorhombic, base-centered orthorhombic, body-centered orthorhombic, and face-centered orthorhombic.
| Bravais lattice | Primitive orthorhombic |
Base-centered orthorhombic |
Body-centered orthorhombic |
Face-centered orthorhombic |
|---|---|---|---|---|
| Pearson symbol | oP | oS | oI | oF |
| Unit cell | 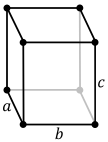
|

|
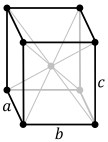
|

|
For the base-centered orthorhombic lattice, the primitive cell has the shape of a right rhombic prism;[1] it can be constructed because the two-dimensional centered rectangular base layer can also be described with primitive rhombic axes. Note that the length of the primitive cell below equals of the conventional cell above.
Crystal classes
[edit]The orthorhombic crystal system class names, examples, Schönflies notation, Hermann-Mauguin notation, point groups, International Tables for Crystallography space group number,[2] orbifold notation, type, and space groups are listed in the table below.
| № | Point group | Type | Example | Space groups | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Name[3] | Schön. | Intl | Orb. | Cox. | Primitive | Base-centered | Face-centered | Body-centered | |||
| 16–24 | Rhombic disphenoidal | D2 (V) | 222 | 222 | [2,2]+ | Enantiomorphic | Epsomite | P222, P2221, P21212, P212121 | C2221, C222 | F222 | I222, I212121 |
| 25–46 | Rhombic pyramidal | C2v | mm2 | *22 | [2] | Polar | Hemimorphite, bertrandite | Pmm2, Pmc21, Pcc2, Pma2, Pca21, Pnc2, Pmn21, Pba2, Pna21, Pnn2 | Cmm2, Cmc21, Ccc2 Amm2, Aem2, Ama2, Aea2 |
Fmm2, Fdd2 | Imm2, Iba2, Ima2 |
| 47–74 | Rhombic dipyramidal | D2h (Vh) | mmm | *222 | [2,2] | Centrosymmetric | Olivine, aragonite, marcasite | Pmmm, Pnnn, Pccm, Pban, Pmma, Pnna, Pmna, Pcca, Pbam, Pccn, Pbcm, Pnnm, Pmmn, Pbcn, Pbca, Pnma | Cmcm, Cmca, Cmmm, Cccm, Cmme, Ccce | Fmmm, Fddd | Immm, Ibam, Ibca, Imma |
In two dimensions
[edit]In two dimensions there are two orthorhombic Bravais lattices: primitive rectangular and centered rectangular.
| Bravais lattice | Rectangular | Centered rectangular |
|---|---|---|
| Pearson symbol | op | oc |
| Unit cell | 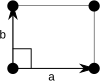
|
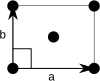
|
See also
[edit]References
[edit]- ^ See Hahn (2002), p. 746, row oC, column Primitive, where the cell parameters are given as a1 = a2, α = β = 90°
- ^ Prince, E., ed. (2006). International Tables for Crystallography. International Union of Crystallography. doi:10.1107/97809553602060000001. ISBN 978-1-4020-4969-9. S2CID 146060934.
- ^ "The 32 crystal classes". Retrieved 2018-06-19.
Further reading
[edit]- Hurlbut, Cornelius S.; Klein, Cornelis (1985). Manual of Mineralogy (20th ed.). pp. 69–73. ISBN 0-471-80580-7.
- Hahn, Theo, ed. (2002). International Tables for Crystallography, Volume A: Space Group Symmetry. International Tables for Crystallography. Vol. A (5th ed.). Berlin, New York: Springer-Verlag. doi:10.1107/97809553602060000100. ISBN 978-0-7923-6590-7.




