Pythagorean hammers

According to legend, Pythagoras discovered the foundations of musical tuning by listening to the sounds of four blacksmith's hammers, which produced consonance and dissonance when they were struck simultaneously. According to Nicomachus in his 2nd-century CE Enchiridion harmonices,[1] Pythagoras noticed that hammer A produced consonance with hammer B when they were struck together, and hammer C produced consonance with hammer A, but hammers B and C produced dissonance with each other. Hammer D produced such perfect consonance with hammer A that they seemed to be "singing" the same note. Pythagoras rushed into the blacksmith shop to discover why, and found that the explanation was in the weight ratios. The hammers weighed 12, 9, 8, and 6 pounds respectively. Hammers A and D were in a ratio of 2:1, which is the ratio of the octave. Hammers B and C weighed 8 and 9 pounds. Their ratios with hammer D were (12:8 = 3:2 = perfect fifth) and (12:9 = 4:3 = perfect fourth). The space between B and C is a ratio of 9:8, which is equal to the musical whole tone, or whole step interval ().
| Hammer | Weight | Interval | Chisel | In C |
|---|---|---|---|---|
| A | 6 | C | ||
| B | 8 | G | ||
| C | 9 | F | ||
| D | 12 | C' |
The legend is, at least with respect to the hammers, demonstrably false. It is probably a Middle Eastern folk tale.[2] These proportions are indeed relevant to string length (e.g. that of a monochord) — using these founding intervals, it is possible to construct the chromatic scale and the basic seven-tone diatonic scale used in modern music, and Pythagoras might well have been influential in the discovery of these proportions (hence, sometimes referred to as Pythagorean tuning) — but the proportions do not have the same relationship to hammer weight and the tones produced by them.[3][4] However, hammer-driven chisels with equal cross-section, show an exact proportion between length or weight and Eigenfrequency.[5]
Earlier sources mention Pythagoras' interest in harmony and ratio. Xenocrates (4th century BCE), while not as far as we know mentioning the blacksmith story, described Pythagoras' interest in general terms: "Pythagoras discovered also that the intervals in music do not come into being apart from number; for they are an interrelation of quantity with quantity. So he set out to investigate under what conditions concordant intervals come about, and discordant ones, and everything well-attuned and ill-tuned."[6] Whatever the details of the discovery of the relationship between music and ratio, it is regarded[7] as historically the first empirically secure mathematical description of a physical fact. As such, it is symbolic of, and perhaps leads to, the Pythagorean conception of mathematics as nature's modus operandi.[8] As Aristotle was later to write, "the Pythagoreans construct the whole universe out of numbers".[9] The Micrologus of Guido of Arezzo repeats the legend in Chapter XX.[10]
-
Dimensions of four Pythagorean hammers.
Contents of the legend
[edit]According to the oldest recorded version[11] of the legend, Pythagoras, who lived in the 6th century BC, sought a tool to measure acoustic perceptions, similar to how geometric quantities are measured with a compass or weights with a scale. As he passed by a forge where four (according to a later version, five) craftsmen were working with hammers, he noticed that each strike produced tones of different pitch, which resulted in harmonies when paired. He was able to distinguish Octave, fifth, and fourth. Only one pair, which formed the interval between fourth and fifth (a major second), he perceived as dissonant. Excitedly, he ran into the forge to conduct experiments. There, he discovered that the difference in pitch was not dependent on the shape of the hammer, the position of the struck iron, or the force of the blow. Rather, he could associate the pitches with the weights of the hammers, which he measured precisely. He then returned home to continue the experiments.
He hung four equally long, equally strong, and equally twisted strings in succession on a peg attached diagonally to the corner of the walls, weighting them differently by attaching different weights at the bottom. Then he struck the strings in pairs, and the same harmonies resonated as in the forge. The string with the heaviest load of twelve units, when paired with the least burdened string carrying six units, produced an octave. Thus, it was evident that the octave was based on the ratio 12:6, or 2:1. The most tense string yielded a fifth with the second loosest string (eight units), and a fourth with the second tightest string (nine units). From this, it followed that the fifth was based on the ratio 12:8, or 3:2, and the fourth on the ratio 12:9, or 4:3. Again, the ratio of the second tightest string to the loosest, with 9:6, or 3:2, yielded a fifth, and the ratio of the second loosest to the loosest, with 8:6, or 4:3, yielded a fourth. For the dissonant interval between fifth and fourth, it was revealed that it was based on the ratio 9:8, which coincided with the weight measurements carried out in the forge. The octave proved to be the product of the fifth and fourth:
Pythagoras then extended the experiment to various instruments, experimented with vessels, flutes, triangles, the Monochord, etc., always finding the same numerical ratios. Finally, he introduced the commonly used terminology for relative pitch.
Further traditions
[edit]With the invention of the monochord to investigate and demonstrate the harmonies of pairs of strings with different integer length ratios, Pythagoras is said to have introduced a convenient means of illustrating the mathematical foundation of music theory that he discovered. The monochord, called κανών (kanōn) in Greek and regula in Latin, is a resonating box with a string stretched over it. A measurement scale is attached to the box. The device is equipped with a movable bridge, which allows the vibrating length of the string to be divided; the division can be precisely determined using the measurement scale. This enables measurement of intervals. Despite the name "monochord", which means "one-stringed", there were also multi-stringed monochords that could produce simultaneous intervals. However, it is unclear when the monochord was invented. Walter Burkert dates this achievement to a time after the era of Aristotle, who apparently did not know the device; thus, it was introduced long after Pythagoras' death.[12] On the other hand, Leonid Zhmud suggests that Pythagoras probably conducted his experiment, which led to the discovery of numerical ratios, using the monochord.[13]
Hippasus of Metapontum, an early Pythagorean (late 6th and early 5th centuries BCE), conducted quantitative investigations into musical intervals. The experiment attributed to Hippasus, involving freely oscillating circular plates of varying thicknesses, is physically correct, unlike the alleged experiments of Pythagoras. It is unclear whether Archytas of Tarentum, an important Pythagorean of the 5th/4th centuries BCE, conducted relevant experiments. He was probably more of a theoretician than a practitioner in music, but he referred to the acoustic observations of his predecessors. The musical examples he cites in support of his acoustic theory involve wind instruments; he does not mention experiments with stringed instruments or individual strings. Archytas proceeded from the mistaken hypothesis that pitch depends on the speed of sound propagation and the force of impact on the sound-producing body; in reality, the speed of sound is constant in a given medium, and the force only affects the volume.[14]
Interpretation of the legend
[edit]Walter Burkert is of the opinion that despite its physical impossibility, the legend should not be regarded as an arbitrary invention, but rather as having a meaning that can be found in Greek mythology. The Idaean Dactyls, the mythical inventors of blacksmithing, were also, according to myth, the inventors of music. Thus, there already existed a very ancient tradition associating blacksmithing with music, in which the mythical blacksmiths were depicted as possessors of the secret of magical music. Burkert sees the legend of Pythagoras in the blacksmiths as a late transformation and rationalization of the ancient Dactyl myth: In the legend of Pythagoras, the blacksmiths no longer appear as possessors of ancient magical knowledge, but rather, without intending to, they become - albeit unknowing - "teachers" of Pythagoras.[15]
In the Early Middle Ages, Isidore of Seville referred to the biblical blacksmith Tubal as the inventor of music; later authors followed him in this. This tradition once again shows the idea of a relationship between blacksmithing and music, which also appears in non-European myths and legends.[16] Tubal was the half-brother of Jubal, who was considered the ancestor of all musicians. Both were sons of Lamech and thus grandsons of Cain. In some Christian traditions of the Middle Ages, Jubal, who observed his brother Tubal, was equated with Pythagoras.[17]
Another explanation is suggested by Jørgen Raasted, following Leonid Zhmud. Raasted's hypothesis states that the starting point of the legend formation was a report on the experiments of Hippasus. Hippasus used vessels called "sphaírai". This word was mistakenly confused with "sphýrai" (hammers) due to a scribal error, and instead of Hippasus' name, that of Pythagoras was used as the originator of the experiments. From this, the legend of the forge emerged.[18]
Basis of music theory
[edit]The whole numbers 6, 8, 9, and 12, in relation to the lowest tone (number 12), correspond to the pure intervals fourth (number 9), fifth (number 8), and octave (number 6) upwards:
| Whole Number | Ratio to the largest number 12 |
Ratio, reduced |
Ratio number | Interval designation |
|---|---|---|---|---|
| 12 | 12:12 | 1:1 | 1.000 | Prime |
| 9 | 9:12 | 3:4 | 0.750 | Fourth |
| 8 | 8:12 | 2:3 | 0.667 | Fifth |
| 6 | 6:12 | 1:2 | 0.500 | Octave |
Such pure intervals are perceived by the human ear as beat-free, as the volume of the tones does not vary. In sheet music, these four Pythagorean tones can, for example, be expressed with the melodic sequence c' – f' – g' – c":

If this sequence of tones is not considered from the lowest, but from the highest tone (number 6), the following intervals also result: a fourth (number 8), a fifth (number 9), and an octave (number 12) - in this case, however, downward:
| Whole Number | Ratio to the smallest number 6 |
Ratio, reduced |
Ratio number | Interval designation |
|---|---|---|---|---|
| 6 | 6:6 | 1:1 | 1.000 | Prime |
| 8 | 8:6 | 4:3 | 1.333 | Fourth |
| 9 | 9:6 | 3:2 | 1.500 | Fifth |
| 12 | 12:6 | 2:1 | 2.000 | Octave |
The fifth and the octave appear in relation to the fundamental tone in natural harmonic series, but not the fourth or its octave equivalent. This interval of a fourth occurs in the ventless brass instruments known since ancient times and in the harmonic overtones of stringed instruments.
Significance for the later development of tonal systems
[edit]The further investigation of intervals consisting of octaves, fifths, and fourths, and their multiples, eventually led from diatonic scales with seven different tones (heptatonic scale) in Pythagorean tuning to a chromatic scale with twelve tones. The wolf intervals in Pythagorean tuning posed a problem: instead of the pure fifths A♭-E♭ and D♭-A♭, the fifths G♯-E♭ and C♯-A♭, which were detuned by the Pythagorean comma, sounded.
With the advent of polyphony in the second half of the 15th century, in addition to the octave and fifth, the pure third became crucial for major and minor triads. Although this tuning could not be realized on a twelve-note keyboard, it could be well achieved in the meantone temperament. Its disadvantage was that not all keys of the circle of fifths were playable. To remedy this deficiency, tempered tunings were introduced, albeit with the trade-off that the pure third sounded harsher in some keys. Nowadays, most instruments are tuned in equal temperament with 12 keys, so that the octaves are perfectly pure, the fifths are almost pure, and the thirds sound rough.
The four Pythagorean tones in music
[edit]In music, the four harmonic Pythagorean tones play a prominent role in the pentatonic scale, particularly on the first, fourth, fifth, and eighth degrees of diatonic scales (especially in major and minor) and in the composition of cadences as fundamental tones of tonic, subdominant, and dominant. This sequence of tones often appears in cadences with the corresponding chords:

The four Pythagorean tones appear in many compositions. The first tones of the medieval antiphons "Ad te levavi" and "Factus est repente" consist essentially of the four Pythagorean tones, apart from some ornaments and high notes.[19]
Another example is the beginning of the Passacaglia in C minor by Johann Sebastian Bach. The theme consists of fifteen tones, of which a total of ten tones and especially the last four tones are derived from the sequence.
Refutation
[edit]Absolute Pitch of Hammers
The resonance frequency of steel hammers that can be moved by human hands is usually in the ultrasonic range and therefore inaudible. Pythagoras could not have perceived these tones, especially when the hammers had a difference of one octave in pitch.
Pitch Depending on Hammer Weight
The vibration frequency of a freely oscillating solid body, such as a longitudinal wave, is usually not proportional to its weight or volume, but it is proportional to its length, which changes with similar geometry only with the cube root of the volume.
For the Pythagorean hammers, the following ratio numbers apply for similar geometry (values in arbitrary units):
| Weight / Volume |
Ratio to largest hammer |
Hammer head length / Vibration frequency |
Ratio to largest hammer | |
|---|---|---|---|---|
| 12 | 1.000 | 2.289 | 1.000 | |
| 9 | 0.750 | 2.080 | 0.909 | |
| 8 | 0.667 | 2.000 | 0.874 | |
| 6 | 0.500 | 1.817 | 0.794 |
Pitch in relation to string tension
The assumption that the vibration frequency of a string is proportional to the tension is not correct. Rather, the vibration frequency is proportional to the square root of the tension. To double the vibration frequency, four times the tension must be applied and thus a weight four times as heavy must be hung on a string.
Physical considerations
[edit]Consonance
[edit]Integer frequency ratios
[edit]| Integer ratio of frequencies |
n | Beat frequency |
|---|---|---|
| 2:1 | 2 | |
| 3:1 | 3 | |
| 4:1 | 4 | |
| 5:1 | 5 |
The fact that a tone with the fundamental frequency is in consonance with a second tone with an integer multiple (with and ) of this fundamental frequency is immediately evident from the fact that the maxima and minima of the tone vibrations are synchronous in time, but can also be explained as follows:
The beat frequency of the two simultaneously sounding tones is mathematically calculated from the difference between the frequencies of these two tones and can be heard as a combination tone:
(see Mathematical description of the beat).
This difference is itself in an integer ratio to the fundamental frequency :
For all integer multiples of the fundamental frequency in the second tone, there are also integer multiples for the beat frequency (see the table on the right), so that all tones sound consonant.
Rational Frequency Ratios
[edit]| Rational ratio of frequencies |
n | Beat frequency |
Fundamental frequency |
|---|---|---|---|
| 2:1 | 1 | ||
| 3:2 | 2 | ||
| 4:3 | 3 | ||
| 5:4 | 4 |
Even for two tones whose frequencies are in a rational ratio of to , there is a consonance. The frequency of the second tone is given by:
Consequently, the beat frequency of the two simultaneously sounding tones is given by:
Under this condition, the fundamental frequency is always an integer multiple of the beat frequency (see the table on the right). Therefore, no dissonance occurs.
Longitudinal Oscillations and Natural Frequency of Solid Bodies
[edit]To estimate a metal block, let's consider a homogeneous rectangular prism with a maximum length and made of a material with a speed of sound . For the vibration mode along its longest side (longitudinal oscillation), it has the lowest natural frequency with antinodes at both ends and a node in the middle.[20]
.
Therefore, the pitch is independent of the mass and cross-sectional area of the prism, and the cross-sectional area can even vary. Moreover, the force and velocity when striking the body also do not play a role. At least this fact corresponds to the observation attributed to Pythagoras that the perceived pitch was not dependent on the hands (and thus the forces) of the craftsmen.
Bodies with more complex geometry, such as bells, cups, or bowls, which may even be filled with liquids, have natural frequencies that require considerably more elaborate physical descriptions since not only the shape but also the wall thickness or even the striking location must be considered. In these cases, transverse oscillations may also be excited and audible.
Hammers
[edit]
A very large sledgehammer (the speed of sound in steel is approximately = 5000 meters per second) with a hammer head length = 0.2 meters has a natural frequency of 12.5 kilohertz. With a square cross-sectional area of 0.1 square meters (0.1 meters by 0.1 meters), it would have an unusually large mass of almost 16 kilograms at a density of 7.86 grams per cubic centimeter. Frequencies above approximately 15 kilohertz cannot be perceived by many people anymore (see auditory threshold); therefore, the natural frequency of such a large hammer is hardly audible. Hammers with shorter heads have even higher natural frequencies that are therefore inaudible.
Anvils
[edit]A large steel anvil with a length = 0.5 meters has a natural frequency of only 5 kilohertz and is therefore easily audible.
There are a variety of compositions in which the composer specifies the use of anvils as musical instruments. Particularly well-known are the two operas from the music drama Der Ring des Nibelungen by Richard Wagner:
- Das Rheingold, Scene 3, 18 anvils in F in three octaves
- Siegfried, Act 1, Siegfried's smithing song Nothung! Nothung! Neidliches Schwert!
Materials with a lower speed of sound than steel, such as granite or brass, produce even lower frequencies with congruent geometry. In any case, anvils are not mentioned in the early accounts and audible sounds of anvils are attributed to hammers in the later versions of the legend.
Metal rods
[edit]

Sound examples of chisels with vibration frequencies that are in integer ratios to each other:
It is possible to compare metal rods, such as chisels used by stonemasons or splitting wedges for stone breaking, in order to arrive at an observation similar to the one attributed to Pythagoras, namely that the vibration frequency of tools is proportional to their weight. If the metal rods, neglecting the tapering cutting edges, all have the same uniform cross-sectional area A but different lengths l, then their weight is proportional to the length and thus also to the vibration frequency, provided that the metal rods are excited to longitudinal vibrations by blows along the longitudinal axis (sound examples can be found in the box on the right).[21]
For bending oscillators, such as tuning forks or the plates of metallophones, different conditions and laws apply; therefore, these considerations do not apply to them.
String vibrations
[edit]
Strings can be fixed at two ends, each on a bridge. Unlike a solid with longitudinal vibrations, the two bridges establish the boundary conditions for two nodal points of vibration; hence, the vibrational node is located in the middle.
The natural frequency and thus the pitch of strings with length are not proportional to the tension , but to the square root of the tension. Moreover, the frequency increases with higher tensile weight and thus higher tension, rather than decreasing:[22]
Nevertheless, the vibration frequency is inversely proportional to the length of the string at constant tension, which can be directly demonstrated with the monochord—allegedly invented by Pythagoras.
Reception
[edit]
Antiquity
[edit]The earliest mention of Pythagoras' discovery of the mathematical basis of musical intervals is found in the Platonist Xenocrates (4th century BC); as it is only a quote from a lost work of this thinker, it is unclear whether he knew the forge legend.[23] In the 4th century BC, criticism of the Pythagorean theory of intervals was already expressed, although without reference to the Pythagoras legend; the philosopher and music theorist Aristoxenus considered it to be false.

The oldest recorded version of the legend was presented centuries after the time of Pythagoras by the Neopythagorean Nicomachus of Gerasa, who in the 1st or 2nd century AD documented the story in his Harmonikḗ Encheirídion ("Handbook of Harmony"). He relied on the philosopher Philolaus, a Pythagorean of the 5th century BC, for his representation of the numerical ratios in music theory.[24]
The famous mathematician and music theorist Ptolemy (2nd century AD) was aware of the weight method transmitted by the legend but rejected it. However, he did not recognize the falsity of the weight experiments; he only criticized their inaccuracies compared to the precise measurements on the monochord.[25] It is probable that he obtained his knowledge of the legendary tradition not from Nicomachus but from an older source, now lost.[26]
The chronologically difficult to place music theorist of the Imperial era, Gaudentius, described the legend in his Harmonikḗ Eisagōgḗ ("Introduction to Harmony"), in a version slightly shorter than that of Nicomachus. The Neoplatonist philosopher Iamblichus of Chalcis, who worked as a philosophy teacher in the late 3rd and early 4th centuries, wrote a Pythagoras biography titled On the Pythagorean Life, in which he reproduced the blacksmith legend in the version of Nicomachus.
In the first half of the 5th century, the writer Macrobius extensively discussed the blacksmith legend in his commentary on Cicero's Somnium Scipionis, which he described in a similar manner to Nikomachos.[27]

The strongest repercussion among the ancient music theorists who took up the narrative was achieved by Boethius with his textbook De institutione musica ("Introduction to Music"), written in the early 6th century, in which he initially describes Pythagoras' efforts of understanding in the forge and then at home.[28] It is unclear whether he relied on Nikomachus' account or another source. In contrast to the entire earlier tradition, he reports five hammers instead of the four assumed by earlier authors. He claims that Pythagoras rejected the fifth hammer because it resulted in dissonance with all the other hammers. According to Boethius' account (as with Macrobius), Pythagoras tested his initial assumption that the difference in sound was due to different strength in the arms of the men by having the smiths exchange hammers, which led to its refutation. Regarding the experiments at Pythagoras' home, Boethius writes that the philosopher first hung strings with weights equal to those of the hammers in the forge and then experimented with pipes and cups, with all the experiments yielding the same results as the initial ones with the hammers. Using the legend as a basis, Boethius addresses the question of the reliability of sensory perceptions in terms of science and epistemology. The crucial point is that Pythagoras was initially prompted by sensory perception to formulate his question and hypotheses, and through empirical testing of hypotheses, he arrived at irrefutable certainty. The path to knowledge went from sensory perception to the initial hypothesis, which turned out to be erroneous, then to the formation of a correct opinion, and finally to its verification. Boethius acknowledges the necessity and value of sensory perception and opinion formation on the path to insight, although as a Platonist, he is inherently skeptical of sensory perception due to its proneness to error. Genuine knowledge, for him, arises only when the regularity is grasped, allowing the researcher to emancipate themselves from their initial dependence on unreliable sensory perception. The judgment of the researcher must not be based solely on sensory judgment derived from empirical experience, but rather it should only be made once they have found a rule through deliberation that enables them to position themselves beyond the realm of possible sensory deception.[29]
In the 6th century, the scholar Cassiodorus wrote in his Institutiones that Gaudentius attributed the beginnings "of music" to Pythagoras in his account of the legend of the blacksmith. He was referring to music theory, as Iamblichus had also done, who, with reference to the blacksmith narrative and the experiments described there, had referred to Pythagoras as the inventor "of music".[30]
Middle Ages
[edit]In the Early Middle Ages, Isidore of Seville mentioned the legend of the blacksmith in his Etymologiae, which became a fundamental reference work for the educated in the Middle Ages. He briefly mentioned the legend, adopting Cassiodorus' wording and also designating Pythagoras as the inventor of music.[31] As Cassiodorus and Isidore were first-rate authorities in the Middle Ages, the notion spread that Pythagoras had discovered the fundamental law of music and thus had been its founder. Despite such sweeping statements, medieval music theorists assumed that music had existed before Pythagoras and that the "invention of music" referred to the discovery of its principles.[32]
In the 9th century, the musicologist Aurelian of Réomé recounted the legend in his Musica disciplina ("Music Theory"). Aurelian's account was followed in the 10th century by Regino of Prüm in his work De harmonica institutione ("Introduction to Harmonic Theory"). Both emphasized that Pythagoras had been given the opportunity to make his discovery in the blacksmith's forge through a divine providence.[33] In antiquity, Nicomachus and Iamblichus had already spoken of a daimonic providence, and Boethius had transformed it into a divine decree.
In the 11th century, the legendary material was processed in the Carmina Cantabrigiensia.[34]

In the first half of the 11th century, Guido of Arezzo, the most famous music theorist of the Middle Ages, recounted the legend of the blacksmith in the final chapter of his Micrologus, basing it on the version of Boethius, whom he named specifically. Guido remarked at the outset: Nor would anyone ever have discovered anything certain about this art (music) if, in the end, divine goodness had not brought about the following event at its behest. He attributed the fact that the hammers weighed 12, 9, 8, and 6 units and thus produced harmonious sound to God's providence.[35] He also mentioned that Pythagoras, starting from his discovery, had invented the monochord, but did not go into detail about its properties.
The work De musica by Johannes Cotto (also known as John Cotton or Johannes Afflighemensis) was illustrated with the blacksmith scene around 1250 by an anonymous book illuminator in the Cistercian Abbey of Aldersbach.[36]
Among the medieval music theorists who told the legend of the forge according to Boethius' version, were also Juan Gil de Zámora (Johannes Aegidius von Zamora), active in the late 13th and early 14th centuries, Johannes de Muris and Simon Tunstede in the 14th century, and Adam von Fulda on the threshold of the early modern period in the 15th century.
As an opponent of the Pythagorean conception, which held that consonances were based on certain numerical ratios, Johannes de Grocheio emerged in the 13th century, starting from an Aristotelian perspective. Although he explicitly stated that Pythagoras had discovered the principles of music, and he told the legend of the forge citing Boethius, whom he considered trustworthy, he rejected the Pythagorean theory of consonance, which he wanted to reduce to a merely metaphorical expression.[37]
Early modern period
[edit]

Franchino Gaffurio published his work Theoricum opus musice discipline ("Theoretical Music Theory") in Naples in 1480, which was revised and republished in 1492 under the title Theorica musice ("Music Theory"). In it, he presented a version of the legend of the forge that surpassed all previous accounts in detail. He based his version on that of Boethius and added a sixth hammer in order to include as many tones of the octave as possible in the narrative. In four pictorial representations, he presented musical instruments or sound generators, each with six harmonic tones, and indicated the numbers 4, 6, 8, 9, 12, and 16 associated with the tones in the labels. In addition to the four traditional ratios of the legend (6, 8, 9, and 12), he added 4 and 16, which represent a tone a fifth lower and another tone a fourth higher. The entire sequence of tones now extends not only over one, but over two octaves. These numbers correspond, for example, to the tones f – c' – f' – g' – c" – f":
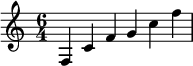
The painter Erhard Sanßdorffer was commissioned in 1546 to create a fresco in the Hessian Büdingen Castle, which is well preserved and represents the history of music starting from the forge of Pythagoras like a compendium.[38]
Gioseffo Zarlino also recounted the legend in his work Le istitutioni harmoniche ("The Foundations of Harmony"), which he published in 1558; like Gaffurio, he based his account on Boethius' version.[39]
The music theorist Vincenzo Galilei, the father of Galileo Galilei, published his treatise Discorso intorno all'opere di messer Gioseffo Zarlino ("Discourse on the Works of Mr. Gioseffo Zarlino") in 1589, which was directed against the views of his teacher Zarlino. In it, he pointed out that the information in the legend about the loading of strings with weights is not accurate.[1]

In 1626, the Thesaurus philopoliticus by Daniel Meisner featured a copper engraving titled "Duynkirchen" by Eberhard Kieser, depicting only three blacksmiths at an anvil. The Latin and German caption reads:[2]
- Triplicibus percussa sonat varie ictibus incus.
- Musica Pythagoras struit hinc fundamina princ(eps).
- The anvil sounds with triple strikes, producing three different tones.
- Music is the foundation built by Pythagoras, which no donkey's head could have achieved.
A few years later, the matter was definitively clarified after Galileo Galilei and Marin Mersenne discovered the laws of string vibrations. In 1636, Mersenne published his Harmonie universelle, in which he explained the physical error in the legend: the vibration frequency is not proportional to the tension, but to its square root.[3]
Several composers incorporated this subject matter into their works, including Georg Muffat at the end of the 17th century.[40] and Rupert Ignaz Mayr.[41]
Modern era
[edit]Even in the 19th century, Hegel assumed the physical accuracy of the alleged measurements mentioned in the Pythagoras legend in his lectures on the history of philosophy.[42]
Werner Heisenberg emphasized in an essay first published in 1937 that the Pythagorean "discovery of the mathematical determinacy of harmony" is based on "the idea of the meaningful power of mathematical structures", a "fundamental idea that modern exact science has inherited from antiquity"; the discovery attributed to Pythagoras belongs "to the strongest impulses of human science in general".[43]
Even more recently, accounts have been published in which the legend is uncritically reproduced without reference to its physical and historical falsehood.[44] For example, in the non-fiction book The Fifth Hammer: Pythagoras and the Disharmony of the World by Daniel Heller-Roazen.[45]
Sources
[edit]- Gottfried Friedlein (Hrsg.): Anicii Manlii Torquati Severini Boetii de institutione arithmetica libri duo, de institutione musica libri quinque. Minerva, Frankfurt am Main 1966 (Nachdruck der Ausgabe Leipzig 1867, online; deutsche Übersetzung online)
- Michael Hermesdorff (Übersetzer): Micrologus Guidonis de disciplina artis musicae, d. i. Kurze Abhandlung Guidos über die Regeln der musikalischen Kunst. Trier 1876 (online)
- Ilde Illuminati, Fabio Bellissima (Hrsg.): Franchino Gaffurio: Theorica musice. Edizioni del Galluzzo, Firenze 2005, ISBN 88-8450-161-X, S. 66–71 (lateinischer Text und italienische Übersetzung)
Further reading
[edit]- Walter Burkert: Weisheit und Wissenschaft. Studien zu Pythagoras, Philolaos und Platon (= Erlanger Beiträge zur Sprach- und Kunstwissenschaft. Band 10). Hans Carl, Nürnberg 1962
- Anja Heilmann: Boethius' Musiktheorie und das Quadrivium. Eine Einführung in den neuplatonischen Hintergrund von "De institutione musica". Vandenhoeck & Ruprecht, Göttingen 2007, ISBN 978-3-525-25268-0, S. 203–222 ([1] at Google Books)
- Werner Keil (Hrsg.): Basistexte Musikästhetik und Musiktheorie. Wilhelm Fink, Paderborn 2007, ISBN 978-3-8252-8359-9, S. 342–346 ([2] at Google Books)
- Barbara Münxelhaus: Pythagoras musicus. Zur Rezeption der pythagoreischen Musiktheorie als quadrivialer Wissenschaft im lateinischen Mittelalter (= Orpheus-Schriftenreihe zu Grundfragen der Musik. Band 19). Verlag für systematische Musikwissenschaft, Bonn–Bad Godesberg 1976
- Jørgen Raasted: A neglected version of the anecdote about Pythagoras's hammer experiment. In: Cahiers de l'Institut du Moyen-Âge grec et latin. Band 31a, 1979, S. 1–9
- Leonid Zhmud: Wissenschaft, Philosophie und Religion im frühen Pythagoreismus. Akademie Verlag, Berlin 1997, ISBN 3-05-003090-9
See also
[edit]References
[edit]- ^ Weiss, Piero, and Richard Taruskin, eds. Music in the Western World: A History in Documents. 2nd ed. N.p.: Thomson Schirmer, 1984. 3. ISBN 9780534585990.
- ^ Kenneth Sylvan Guthrie, David R. Fideler (1987). The Pythagorean Sourcebook and Library: An Anthology of Ancient Writings which Relate to Pythagoras and Pythagorean Philosophy, p.24. Red Wheel/Weiser. ISBN 9780933999510.
- ^ Christensen, Thomas, ed. The Cambridge history of Western music theory. Cambridge: Cambridge University Press, 2002. 143. ISBN 9780521623711.
- ^ Burkert, Walter (1972). Lore and Science in Ancient Pythagoreanism, p.375. ISBN 9780674539181. Cited in Christensen 2002, p.143.
- ^ Markus Bautsch: Über die pythagoreischen Wurzeln der gregorianischen Modi, English: About the Pythagorean roots of the Gregorian modes, Mater Dolorosa (Berlin-Lankwitz), March 2012, retrieved on 31 August 2017
- ^ Barker (2004). Andrew (ed.). Greek musical writings (1st pbk. ed.). Cambridge: Cambridge University Press. p. 30. ISBN 978-0-521-61697-3.
- ^ Lucas N.H. Bunt; Phillip S. Jones; Jack D. Bedient (1988). The historical roots of elementary mathematics (Reprint ed.). New York: Dover Publications. p. 72. ISBN 978-0-486-25563-7.
- ^ Christian, James (26 January 2011). Philosophy An Introduction to the Art of Wondering. Wadsworth Pub Co. p. 517. ISBN 978-1-111-29808-1.
- ^ Waterfield, transl. with commentary by Robin (2000). The first philosophers : the Presocratics and Sophists (1. publ. as an Oxford world's classics paperback ed.). Oxford: Oxford Univ. Press. p. 103. ISBN 978-0-19-282454-7.
the pythagoreans construct the whole universe out of numbers.
- ^ "GUIMICB_MBBR2784". chmtl.indiana.edu. Retrieved 2023-05-09.
Erant antiquitus instrumenta incerta. et canentium multitudo sed ceca. Nullus enim hominum uocum differentias. et simphoniae descriptionem poterat aliqua argumentatione colligere. neque posset unquam certum aliquid de hac arte cognoscere. nisi diuina pietas tandem quod sequitur suo nutu disponeret. Cum Phitagoras quidam magnus philosophus forte iter ageret. uentum est ad fabricam. in qua super unam incudem quinque mallei feriebant. Quorum suauem miratus concordiam philosophus accessit. primumque in manuum uarietate sperans [f.20r] uim soni ac modulationis existere. mutauit malleos. Quo facto. sua uis quemque secuta est. Subtracto itaque uno qui dissonus erat a ceteris. alios ponderauit. Mirumque in modum diuino nutu primus .XII. secundus .VIIII. tertius .VIII. quartus .VI. nescio quibus ponderibus appendebant. Cognouit itaque in numerorum proportione et collatione musicae uersari scientiam. Erat enim ea constitutio in quattuor malleis. quae modo est in quattuor litteris .A.D.E.a. Denique si A habeat .XII. et D VIIII. sintque quaternarii in pro passu. habebit .A. in .XII. ternarios .IIII. et D. in .VIIII. ternarios .III. Ecce diatessaron. Rursus cum habeat A .XII. si teneat E. VIII. quaternarios passus tres habebit .A. duos uero E. et diapente patet. Sint iterum .XII in A. et .VI. in alteram a. Senarius medietas est duodenarii. sicut et a acuta alterius A medietate colligitur. Adest ergo diapason. Cum igitur ipsa .a. ad D. diatessaron ad e diapente. alteri uero a diapason reddit. D quoque ad e tonum. ad utrumque A a diatessaron. et diapente sonat. Et E etiam ad D. tonum utrique A.a. diapente et diatessaron mandat. a uero acuta cum A diapason. cum D diapente. cum E diatessaron sonat. quae in supra dictis numeris curiosus perscrutator inuenit. Hinc enim incipiens Boetius panditor huius artis. multam miramque et difficillimam huius artis cum numerorum proportione concordiam demonstrauit. [f.20v] Quid plura? Per supra dictas species uoces ordinans. monocordum primus ille Phitagoras quattuor neruorum composuit. in quo quia non est lasciuia. sed diligenter aperta artis notitia. sapientibus in commune placuit. atque usque in hunc diem ars paulatim crescendo conualuit. ipso doctore semper humanas tenebras illustrante. cuius summa sapientia per cuncta uiget secula.
- ^ Nikomachos von Gerasa, Handbook of Harmonics 6, translated by Anja Heilmann: Boethius' Music Theory and the Quadrivium, Göttingen 2007, pp. 345–347, cited literally in Iamblichos von Chalkis, On Pythagorean Life 115–121, translated by Michael von Albrecht: Iamblichus. Pythagoras: Legend – Doctrine – Way of Life, Darmstadt 2002, pp. 109–113.
- ^ Walter Burkert: Weisheit und Wissenschaft, Nuremberg 1962, p. 353 and note 28.
- ^ Leonid Zhmud: Wissenschaft, Philosophie und Religion im frühen Pythagoreismus, Berlin 1997, pp. 193–196; see also Barbara Münxelhaus: Pythagoras musicus, Bonn–Bad Godesberg 1976, pp. 28 f.
- ^ Walter Burkert: Weisheit und Wissenschaft, Nuremberg 1962, pp. 362–364; Leonid Zhmud: Wissenschaft, Philosophie und Religion im frühen Pythagoreismus, Berlin 1997, pp. 196–199. Skepticism regarding Archytas' acoustic experiments is expressed by Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, pp. 129–148; see also pp. 473–475. He points out that Archytas mainly relies on information from his predecessors and everyday experience.
- ^ Walter Burkert: Weisheit und Wissenschaft, Nuremberg 1962, p. 355.
- ^ Walter Burkert: Weisheit und Wissenschaft, Nuremberg 1962, p. 355; Barbara Münxelhaus: Pythagoras musicus, Bonn–Bad Godesberg 1976, pp. 38 f., 46.
- ^ James W. McKinnon: Jubal vel Pythagoras, quis sit inventor musicae? In: The Musical Quarterly, vol. 64, no. 1, 1978, pp. 1–28; Paul E. Beichner: The Medieval Representative of Music, Jubal or Tubalcain? (= Texts and Studies in the History of Mediaeval Education 2), Notre Dame, Indiana, 1954; Francis Olivier Zimmermann: La forge et l'harmonie. De Pythagore à Tubalcain et Jubal. In: Zimmermann: Orphée: arts vivants, arts de parole et mélodie (online).
- ^ Jørgen Raasted: "A neglected version of the anecdote about Pythagoras's hammer experiment." In: Cahiers de l'Institut du Moyen-Âge grec et latin 31a, 1979, pp. 1–9, here: 6 f.; Leonid Zhmud: "Wissenschaft, Philosophie und Religion im frühen Pythagoreismus", Berlin 1997, p. 192. (Translated from German)
- ^ See Factus est repente, Word-melody relationships in Gregorian chant; Der erste Gesang des Kirchenjahres.
- ^ Ludwig Bergmann, Clemens Schaefer: Lehrbuch der Experimentalphysik. Band 1, 9. Auflage. Berlin 1974, Kapitel 83: Schallsender, Abschnitt Longitudinalschwingungen.
- ^ Markus Bautsch: Über die pythagoreischen Wurzeln der gregorianischen Modi (online).
- ^ Ludwig Bergmann, Clemens Schaefer: Lehrbuch der Experimentalphysik. Band 1, 9. Auflage. Berlin 1974, Kapitel 83: Schallsender, Abschnitt Saite.
- ^ Xenocrates Fragment 9 H. See Walter Burkert: Weisheit und Wissenschaft, Nuremberg 1962, p. 57 and Leonid Zhmud: Wissenschaft, Philosophie und Religion im frühen Pythagoreismus, Berlin 1997, p. 193.
- ^ This passage from Nicomachus' work is edited, translated into English, and commented on by Carl A. Huffman: Philolaus of Croton, Cambridge 1993, pp. 145–165.
- ^ Barbara Münxelhaus: Pythagoras musicus, Bonn–Bad Godesberg 1976, p. 52.
- ^ Walter Burkert: Weisheit und Wissenschaft, Nuremberg 1962, p. 355.
- ^ Macrobius, Commentarii in somnium Scipionis 2,1,8–13.
- ^ Boethius, De institutione musica 1,10–11, translated by Anja Heilmann: Boethius' Musiktheorie und das Quadrivium, Göttingen 2007, pp. 342–345.
- ^ For the scientific and epistemological background, see Anja Heilmann: Boethius' Musiktheorie und das Quadrivium, Göttingen 2007, pp. 205–218.
- ^ Cassiodorus, Institutiones 2,5,1; cf. Iamblichus, De vita Pythagorica 121.
- ^ Isidore, Etymologiae 3,16,1.
- ^ Barbara Münxelhaus: Pythagoras musicus, Bonn–Bad Godesberg 1976, pp. 15–17.
- ^ Hans Martin Klinkenberg: Der Verfall des Quadriviums im frühen Mittelalter. In: Josef Koch (ed.): Artes liberales. Von der antiken Bildung zur Wissenschaft des Mittelalters, Leiden 1976, pp. 1–32, here: 24 f.
- ^ Carmina Cantabrigiensia, Song 45 and Pythagoras sequence (first half of the 11th century); see Walther Kranz: Pythagoras in the Carmina Cantabrigiensia (online; PDF; 2.3 MB).
- ^ Guido of Arezzo, Micrologus 20 (German translation online).
- ^ Aldersbach Collection Manuscript, Clm 2599, fol. 96v, Bayerische Staatsbibliothek, Munich
- ^ Barbara Münxelhaus: Pythagoras musicus, Bonn–Bad Godesberg 1976, p. 16, 76; Frank Hentschel: Sinnlichkeit und Vernunft in der mittelalterlichen Musiktheorie, Stuttgart 2000, pp. 148–150 (online).
- ^ Walter Salmen: Musikleben im 16. Jahrhundert (Music Life in the 16th Century), Leipzig 1976; black and white photograph online.
- ^ Werner Keil (ed.): Basistexte Musikästhetik und Musiktheorie (Basic Texts on Music Aesthetics and Music Theory), Paderborn 2007, p. 56 (translation of Zarlino's text).
- ^ Georg Muffat: Nova Cyclopeias Harmonica (1690).
- ^ Rupert Ignaz Mayr: Pythagorische Schmids-Fuencklein (1692).
- ^ Werner Keil (ed.): Basistexte Musikästhetik und Musiktheorie, Paderborn 2007, p. 343.
- ^ Werner Heisenberg: Gedanken der antiken Naturphilosophie in der modernen Physik. In: Werner Heisenberg: Wandlungen in den Grundlagen der Naturwissenschaft, 8th edition, Stuttgart 1949, pp. 47–53, here: 50.
- ^ Arnold Keyserling: Geschichte der Denkstile. 3. Das logische Denken (online); Karl Sumereder: Musik und Mathematik (online); Arnold Keyserling: Der neue Name Gottes. Die Weltformel und ihre Analogien in der Wirklichkeit, Vienna 2002, p. 71 (Pythagorean hammers, p. 71, at Google Books).
- ^ Daniel Heller-Roazen: The Fifth Hammer: Pythagoras and the Disharmony of the World, Frankfurt am Main 2014, pp. 14–22 (online).




































