Jump to content

Talk:0.999.../Archive 9

Page contents not supported in other languages.
From Wikipedia, the free encyclopedia
Archive 5←Archive 7Archive 8Archive 9Archive 10Archive 11→Archive 15

Untitled

DO NOT EDIT OR POST REPLIES TO THIS PAGE. THIS PAGE IS AN ARCHIVE.

This archive page covers approximately the dates between 2006-06-29 and 2006-09-09.

Post replies to the main talk page, copying or summarizing the section you are replying to if necessary.

Please add new archivals to Talk:Proof that 0.999... equals 1/Archive10. (See Wikipedia:How to archive a talk page.)

How about a conceptual "proof" by the Socratic method?

Is it true that every real number has an infinite decimal expansion?

Yes.

And given two different real numbers as infinite decimal expansions, can you tell whether one is greater or less than the other.

Yes, I think so.

How would you do this?

Compare each expansion, number by number in sequence. When we encounter a number in the expansion of one which is different from the other, then we may say that the first real number is greater or less according as the number is greater or less.

And when are two numbers equal?

They are equal if this process never terminates. That is, if each digit in one sequence is equal to each corresponding digit in the other.

And so, using this method, would you then say that 0.999... is less than, greater than, or equal to 1?

Clearly, it must be less, for 0.999... begins with a 0, while 1 begins with a 1.

Good. Now I will demonstrate the flaw in your method of comparison. Are you aware that numbers may be represented as points on a line?

Yes.

And a pair of real numbers are equal exactly when the points they represent coincide?

Yes.

What if the two numbers are unequal?

Then the points they represent must be different.

If two different points on a line are given, then there is a third point between them which is not equal to either of the other two. Is this reasonable?

Yes.

Very well then. So according to your claim that 0.999... is different from 1, there must be a point between the two which is not equal to either.

That is correct.

And this third point must be greater than 0.999... and less than 1, without being equal to either?

Yes.

So using your method of comparison, what is the first digit of this point?

If by first digit, you mean the digit to the left of the decimal point, then it must be a zero since it has to be less than 1.

Yes, that's what I meant. What about the first digit to the right of the decimal point? Is it less than 9, greater than 9, or equal to 9?

It cannot be less than 9, since this would make it less than 0.999... by the method of comparison. It cannot be greater than 9, because each digit is an integer less than 10. So it must equal nine.

So here is the number you have so far produced for me: 0.9????... where the digits represented by a "?" are yet to be determined. What is now the second digit to the right of the decimal place?

Again, it must equal 9, since it cannot be less as that would make the number less than 0.999..., and it cannot be greater for there is no individual digit greater than 9.

Here is the number so far: 0.99???... Do you see that the argument you have just offered must apply to each digit, taken in turn, of this expansion?

Yes, I do.

Then applying this argument, we can conclude that the number between 0.999... and 1 which is not equal to either of them is 0.999...

That is correct.

But 0.999... is equal to 0.999..., is it not?

Yes, it is.

But by your argument, this is the only number between 0.999... and 1 which is unequal to either. So from this perspective 0.999... must be unequal to 0.999..., which is absurd. What is the problem?

I must have made a mistake.

Look carefully at the assumptions you have made.

At the outset, I assumed that two real numbers are comparable according to their sequences of digits. Then I assumed that between any two different numbers, there lies a third which is also different. These two assumptions must be incompatible in some way.
This is certainly good, as well as comprehensive and understandable to the layperson, but I think its a little too long for the article. -- He Who Is[ Talk ] 16:06, 29 June 2006 (UTC)


You could explain it in a shorter (but less well laid out way) and then it would not be too long. You could say "Between any two distinct real numbers there must be another number which is larger than one of them, but not as large as the other. There can be no numbers between 0.999... and 1, so they must have the same value." Or an alternative way of looking at it "All numbers can be placed on the number line. If two points are in the same place on the number line they are the same number, if they are in different places they are different numbers. If you place 0.999... and 1 on the number line they appear to be in the same place. If you zoom in on the number line these two points still appear to be in the same place. If you zoom in by an infinite amount one still appears to be on top of the other. Therefore they must be the same number." (I expect both of these ideas have been suggested before and probably rejected because they are not rigorous enough. They are however good for trying to convince people who do not believe that 0.999...=1.) Raoul Harris 16:33, 29 June 2006 (UTC)
This is a version of the argument I have nicknamed the "squeeze proof". Many variations of this can be found on the web, though a lengthy Socratic dialog is unusual. Having read far too many debates in researching this article, I noticed that I balked early on here at the sentence, "They are equal if this process never terminates." The typical reader neither uses nor feels comfortable with this language. (Nor with zooming in by an infinite amount!) Also, it gets us into dangerous territory. For example, a natural question it raises is, "How long do we have to wait to decide equality?" And the answer would seem to be, "Forever!" Not quite what we were going for, eh? In fact, one of the core mental errors people have in this area is a conception of limits as a process rather than a static fact. They want a definite answer sometime before they die, so they artificially terminate the process — and reach the wrong conclusion.
A less conversational, though more rigorous, use of the same idea is embodied in the "order proof". Here's its last paragraph, looking for a rational between 0.999… and 1:
  • If an upper bound less than 1 exists, it can be written as 1−x for some positive rational x. To bound 9⁄10, which is 1⁄10 less than 1, x can be at most 1⁄10. Continuing in this fashion through each decimal place in turn, induction shows that x must be less than 1⁄10n for every positive integer n. But the rationals have the Archimedean property (they contain no infinitesimals), so it must be the case that x = 0. Therefore U(S) = U({1}), and 0.9999… = 1.
Here the Archimedean property plays a decisive role. You might say it tells us we don't actually have to compare forever, so long as we are prepared to compare as much as needed on demand. For those who have studied calculus, the same kind of subtle but effective termination appears in the "epsilon-delta" technique.
Picture two kids playing a game of "name the largest number". The first says "one hundred", the second responds "one hundred and one", the first goes for "one bazillion", and the second counters with "one bazillion and one!" The game gets boring quickly; the kids needn't play forever to realize that there is no largest number.
Now take reciprocals: The immediate implication is that there is no smallest positive rational. The version of the Archimedean property used here tells us that if a non-negative rational number is smaller than any positive rational we can name, we have only one choice: zero.
I'm not confident of my ability to put that into a Socratic dialog! Nor would I say it is "obvious", for two reasons. One reason is that I've seen too many nay-sayers who want to insist on the existence of infinitesimals. The other is that we are perfectly capable of constructing number systems that somewhat resemble the rationals (or reals), but that do include infinitesimals: they are non-Archimedean. (The article later mentions a few.) I doubt many nay-sayers would actually want to use such numbers, but to realize that, they would have to confront some of the awkward implications. --KSmrqT 19:18, 29 June 2006 (UTC)
Well, you're spot on about the problem of non-termination. I did realize that little hitch when I wrote the dialog. But, honestly, pretend you aren't a mathematician for a moment. You don't know a lick of calculus: you are the "boy" in the Socratic dialog Meno. Try to answer the question naïvely: how do you decide on the equality of two decimal expansions? Invariably, the answer you come up with is going to be inconsistent with the "geometry" of R (i.e., the Archimedean property). Silly rabbit 19:41, 29 June 2006 (UTC)
Actually, the very term "decide" is problematic, as I'm sure you (the mathematician) are aware. The article may want to include some indication of these philosophical issues. Silly rabbit 19:46, 29 June 2006 (UTC)
Anyway, the offending passage of the dialog can easily be swept away. The student could answer something along the lines of: "They are equal if the one is neither less than nor greater than the other." Of course a consequence is that ultimately one must face the possibility of non-termination in the case of equality. It also fails to highlight the student's "error" in stark terms. Silly rabbit 20:55, 29 June 2006 (UTC)
Thoroughly excellent! I was about to ask about this, whether the 'find a number between 0.999... and 1' is a proof or just a sneaky way to explain this to people. There is no number between 0.9999.... and 1 (because you can't just add another '9' in the trailing 9's), thus the two numbers are equivalent. *applaud* Piepants 20:39, 1 September 2006 (UTC)Piepants

But what about 1=0.999...?

This is not a problem with the article but with the wiki search engine. Searching for "1=0.999..." or "1 equals 0.999..." doesn't return anything usable. Could someone make a link from the inverted titles to this article so that "=" may become commutative again? Thx. 82.135.2.13 01:17, 10 August 2006 (UTC)

Typing "Proof that 1 equals 0.999..." etc returns this article on the search though, but you need to use "proof". —Mets501 (talk) 01:28, 10 August 2006 (UTC)

Back on the horse

Okay, since I was last seen here, I've lined up some half-dozen references. First up, and the most exciting, is a fresh look at one of the first sources ever to be mentioned on this talk page: Fred Richman. He uses Dedekind cuts in a way that avoids partitions, upper bounds, the U operator, and induction. And it turns out that he actually did this not just on his personal homepage, but in an MAA pedagogical publication! After I hit "Save page" on this comment, I'll hit "Save page" on the "Order proof" section of the article. It will be different, but hopefully not so different that it precipitates any bloodshed. Melchoir 22:06, 23 August 2006 (UTC)

Now that you've finally convinced yourself that a direct Dedekind cut approach is not OR, it seems a good time to mention the three-volume series Fundamentals of Mathematics, from MIT Press. In the first volume, Foundations of Mathematics: The Real Number System and Algebra, Chapter 1, "Construction of the System of Real Numbers" G. Pickert and L. Görke provide several approaches. They first demonstrate an approach using decimal expansions, but note "addition can only be defined in a very lengthy way, and the rules for calculation are not very convenient to prove." They then note the fact that "a0.a1a2a3… is the least upper bound of the set of rn." (For decimal expansions, rn has previously been defined as rn = ∑i=0…n ai 10−i.)
Motivated by this observation, they define Dedekind cuts, with most authors, as a partition of the rationals satisfying certain properties. And so on. I took the liberty of cutting through the voluminous discussion to distill the parts relevant to this article, but the arguments — including the pivotal role of the Archimedean property — are essentially theirs.
Your proof incorrectly states the Archimedean property as the lack of infinite rational numbers, when it actually is the lack of infinitesimal rationals; and it's clearly not just a typo. It is also puzzling to see the name "cut" applied to a single set, rather than a pair of sets partitioning the rationals. Logically, the second set is merely the complement of the first in the reals and so would seem to convey no additional information; however, things are not so simple. Also, standard reals are rather forgiving, but in advanced treatments there are subtleties. For example, Goldblatt, Topoi, the categorial analysis of logic, in section 14.8 discusses the fact that in many topoi not only are the reals defined by a "Cauchy" approach different from those defined by a "Dedekind" approach, but slight variations in the demands on a cut are also of interest. I'll quote Goldblatt's definition.
In Set, a real number r∈R is uniquely determined by the sets
Ur = {c∈Q: r < c}
Lr = {c∈Q: r > c},
called the upper and lower cut of r. In general an ordered pair ⟨U,L⟩∈𝒫(Q)×𝒫(Q) of subsets of Q is called a Dedekind real number if it satisfies the sentences
  1. ∃v∃w(vεU∧wεL) "non-empty"
  2. ∀v~(vεU∧vεL) "disjoint"
  3. ∀v(vεL≡∃w(wεL∧w>v)) "open lower cut"
  4. ∀v(vεU≡∃w(wεU∧w<v)) "open upper cut"
  5. ∀v∀w(v>w⊂vεU∨wεL) "close together"
where the symbols U and L denote the subsets U and L, ε denotes the standard membership relation, and the variables v and w range over the members of Q. For such a pair ⟨U,L⟩ there is one and only one real number r∈R with U = Ur and L = Lr.
Here we're in the context of topos logic, and we need to keep our wits about us. But classical logic is a special case, so for present purposes we can interpret simply. Anyway, the thing to realize is that we can't really define Ur and Lr using a comparison operator, because we haven't yet defined the reals. And for that we want pairs satisfying the five sentences.
Anyway, I hope this is a sign that we are converging, and I do think the Richman paper is a nice addition.
I'm intending a minor rewrite pass over the whole article to fix some of the mess that has accumulated, but I've been postponing it while I work on other things. I'll hang on to a copy of your variation and see what of it I can profitably use. --KSmrqT 00:36, 24 August 2006 (UTC)
For convenience, I'll stick the variation here.

Order proof

The step from rationals to reals is a huge extension, and order is an essential part of any construction. In the Dedekind cut approach, each real number x is the infinite set of all rational numbers that are less than x.[1] In particular, the real number 1 is the set of all rational numbers that are less than 1.[2]

Every positive decimal expansion then easily determines a Dedekind cut: the set of rational numbers which are less than some stage of the expansion. So the real number 0.999... is the set of rational numbers r such that r < 0, or r < 0.9, or r < 0.99, or r is less than some other number of the form 1 − (1⁄10)n.[3]

The equation "0.999... = 1" means that these two Dedekind cuts are the same set, each containing the same rational numbers. If the equation were untrue, there would have to be some rational number r such that r < 1, but r > 1 − (1⁄10)n for every positive integer n. Defining q to be the rational number 1 / (1 − r), one would have q > 10n for every n, which is impossible. (There is no infinite rational number; the rational numbers are Archimedean.) So 0.999... = 1.

This approach to assigning a real number to each decimal expansion is due to an expository paper titled "Is 0.999 ... = 1?" by Fred Richman in Mathematics Magazine, which is targeted at undergraduate mathematicians.[4] Richman notes that taking Dedekind cuts in any dense subset of the rational numbers yields the same results; in particular, one can use decimal fractions, for which the proof is more obvious.[5] Other modifications of the procedure can lead to structures other than the real numbers; see below.

This will save digging through the history. --KSmrqT 00:47, 24 August 2006 (UTC)
You reverted me because the definitions of "Dedekind cut" and "Archimedean" I found in the literature are different from the ones you personally prefer? One of them already has a citation to two references. I will add a citation for the other. If you have further questions, please direct them here before reverting anything. Melchoir 00:52, 24 August 2006 (UTC)
Like you did? You reverted once while I was typing extended material here, and a second time immediately after. In any event, as I said to you on my talk page I'm winding down for the day. Further discussion or revert wars or whatever will just have to wait, at least on my end. --KSmrqT 02:23, 24 August 2006 (UTC)
I have already asked my question of the old material several times: "Are there sources for this"? The answer was no, and I made sure of that before taking any action. If you extend me the same courtesy by exercising a little caution, we can be civilized about this. Melchoir 02:41, 24 August 2006 (UTC)
You distort the history. The chorus of answers to your old questions was "Stop calling standard mathematics Original Research." It was clear from your attitude at the time that you were extremely hostile and that such a citation would accomplish nothing. Then, too, I expended considerably words trying to talk with you before I walked away in frustration, leaving others to deal with you.
The current article is worse than when I left it, as predicted. The number of footnotes is absurd, especially when we have separate articles on the cited topics, such as Dedekind cut, Cauchy sequence, construction of real numbers, Archimedean property, and so on. I could say much more, but why?
This section did not need to be rewritten just to satisfy your obstinacy, and the rewrite has several problems which I will not waste more time discussing if you have not changed your attitude. --KSmrqT 12:41, 24 August 2006 (UTC)
My stated goal is to make this a Featured Article. Other theories on my motivation and behavior are welcome at User talk:Melchoir, where I will be eager to discuss them.
We cannot rely upon the four articles you mentioned for verification because, for various reasons, Wikipedia does not consider itself a reliable source. When there are multiple ways of formulating a concept, or an accuracy dispute between editors, it is especially important to seek external verification.
Still, the number of footnotes is easily reduced by combining some of them, particularly those that cite the same author within a given paragraph. I'll work on that now... Melchoir 14:50, 24 August 2006 (UTC)
There. The number of footnotes is only two less. But now, every cite appears at the end of a sentence, and each paragraph has at least one and no more than two. I suggest that this is not absurd. Melchoir 15:04, 24 August 2006 (UTC)
Another absurd twist. I will again revert to my decision to ignore you, and my plan to rewrite the article at some point in the future to clean out the mess you have almost single-handedly created. --KSmrqT 20:28, 24 August 2006 (UTC)
What are you talking about? Melchoir 20:39, 24 August 2006 (UTC)
Or, absent an answer to that, what needs rewriting, and why? Melchoir 22:03, 24 August 2006 (UTC)

Moving along...

Well, I think "Order proof" and "Limit proof" are looking good. Next, that geometric series is getting lonely, so I'll be adding a complementary method in "Real analysis" using subdivided intervals, due to Bartle and Sherbert.

Then "Other number systems" could use more explicit ties to 0.999..., including a subsection on systems where "0.999..." doesn't mean 1: hackenstrings and Richman's "Cut D". Possibly the 10-adic expression ...999 could make an appearance somewhere. "Applications" could use a second application to justify the plural: perhaps the role of the converse in the decimal proof that the reals are uncountable? "In popular culture" needs a bit of expansion, and finally-- this is the hard part, but doable-- the introductions of the three major proof sections should start explaining their contexts: the desirability of theorems with weak hypotheses, and the diversity of pedagogical treatments of real numbers. Any takers for those tasks?

After all that, I'm thinking GA -> cook up some illustrations -> Peer Review -> FA -> Main Page -> peace and love.

In local news, I don't have a history book on hand. Can anyone fill in the details on the origin of the geometric series formula and its early proofs? Melchoir 18:39, 25 August 2006 (UTC)

Okay, nested intervals is up. I'm not real comfortable with having two long-yet-dense paragraphs that don't address 0.999..., so perhaps they should be exported to another article and allowed to expand. Melchoir 23:12, 25 August 2006 (UTC)

Calc Thingy

[[Image:0999.png|right|thumb|A calculator having trouble with 0.999...]] What's wrong with using this image to illustrate the point-- all but made by Mazur, especially if you read the book-- that a student who relies on a calculator is screwed when it comes to reasoning about 0.999...? Melchoir 20:57, 29 August 2006 (UTC)

The point is that the calculator doesn't recognize that character, not that the calculator can't do it (it can't anyway, but that's not what the picture is saying). It's like typing in 3×5 into a calculator that's looking for 3*5 and then saying that calculators struggle with multiplication. —Mets501 (talk) 21:14, 29 August 2006 (UTC)
I'm not sure that there's really a relevant difference between not recognizing the characters and not being able to execute the task. The whole danger with calculators as a thinking aid is that you don't have to interpret for them: they're supposed to be able to take an input as it looks on your page and give you the answer. I'm not aware of any calculator that inputs either three dots or an ellipsis and doesn't choke. As for syntax, I don't think we have to worry about a reader who thinks, "Well, if they'd put spaces between the dots, maybe it would have worked"!
Maybe the "trouble" language is sending the wrong message. How about, "A typical calculator cannot help one reason with 0.999...?" Melchoir 21:28, 29 August 2006 (UTC)
Definitely better. Include "typical" though, because calculators such as the TI-89 can do it if entered as an infinite series. —Mets501 (talk) 02:43, 30 August 2006 (UTC)
True, yet even a TI-89 requires its operator to do much of the interpretation for it. Okay, I'll try the second version. Melchoir 05:54, 30 August 2006 (UTC)

Dual numbers: not ordered?

It seems pretty clear to me that you can make the dual numbers into an ordered ring, such that epsilon is a true infinitesimal. So what's the deal with:

  • "However, the infinitesimals are displaced off the real line, rather than ordered between standard reals."?

Is that saying, possibly, that one applies the topology of the plane and not the natural order topology? If so, wouldn't 0.999… still be well-defined and equal to 1, just as in the regular complex numbers? Is there a source that addresses decimal expansions in these sets, anyway? Melchoir 16:38, 30 August 2006 (UTC)

Meh, I'll remove it to here:

Standard reals can also be extended to become dual numbers, by including a new element ε defined to combine with other reals in the usual way, but such that its product with itself is zero. Every dual number then consists of a standard real component and an "infinitesimal" component, a+bε, either of which may be zero. However, the infinitesimals are displaced off the real line, rather than ordered between standard reals.

Melchoir 06:36, 31 August 2006 (UTC)

In fact, this is plainly a confusion; the dual numbers can be viewed as a plane, but they can also be ordered lexicographically, in which case they clearly have non-Archimedian elements and 1 - kε lies between 0.9999...9 and 1 (so the limit is undefined). This order has the property that all sums of squares are positive, but of course it is not a field. We need merely leave the bit about displacement out.
Right, I'm on board with you mathematically. But does anyone actually work with the dual numbers in the order topology? It seems to me that physicists would be much happier taking limits in the plane instead. Melchoir 15:03, 31 August 2006 (UTC)
...ah, it looks like the computer science people are interested in our ordering. One moment... Melchoir 15:12, 31 August 2006 (UTC)
...Okay, in addition to the reference I used just now, I also found "A sheaf of R-algebras on the set of Dual Numbers", whose author uses an "obvious and useful" metric topology and notes that other authors use different topologies. Of course, nobody is saying anything about 0.999…. Maybe we should just leave it the way it is and avoid drawing any conclusions. Melchoir 15:44, 31 August 2006 (UTC)

And the p-adics

Why are the p-adic numbers offered as an example of an ordered algebra that is non-Archimedean? Isn't it true that the p-adics can't be ordered, and no p-adic has an infinitesimal norm? Melchoir 16:52, 30 August 2006 (UTC)

I've moved the tag to the sentence this seems to be objecting to. I'm not sure whether the p-adics are an ordered field, but they certainly have a natural order: lexicographic, first on the multiples of 1, then on the multiples of p, then on the multiples of p2; so in the 3-adics,
0 < 3 < 6 < 1 < 4 < 7 < 2... Septentrionalis 17:15, 30 August 2006 (UTC)
Interesting! Anyway, p-adic number claims that "This field cannot be turned into an ordered field." I'm no expert in this area, but I'm inclined to believe it.
For this article, perhaps we'll change "orderings" to "metrics" and segregate the p-adics into a new third section of "Other number systems" dedicated to systems where decimal expansions don't make sense, but which are still somehow relevant? Melchoir 17:25, 30 August 2006 (UTC)
(By the way, I chose words poorly, but I secretly do know the difference between a field that's an ordered set, and an ordered field.) Melchoir 17:28, 30 August 2006 (UTC)

I've tried moving them to a new subsection and motivating them through Gower's discussion of 0.000…1. I don't have a reference for ...999 = −1, but given the number of books on the p-adics and the obviousness of using negative one as an example, I'm sure there's a citation waiting to be found. Melchoir 19:50, 30 August 2006 (UTC)

This is what I get for not owning a history book... I could swear that the construction of the reals by Cauchy sequences was due to Cantor. Are you sure it isn't? Melchoir 20:39, 30 August 2006 (UTC)

...and MacTutor comes through again. Melchoir 21:02, 30 August 2006 (UTC)

I've got three or four sources for the p-adics now. This is going to kick ass... Melchoir 08:35, 31 August 2006 (UTC)

There, now the reader's head is guaranteed to explode, and it's all true! Melchoir 18:09, 31 August 2006 (UTC)

Archive 08

The new archive's date isn't a typo; I went from the absolute earliest post to the absolute latest post. By a freak coincidence, someone replied to a two-month old discussion while I was moving the text, so I had to move that section back. Supadawg (talk • contribs) 20:51, 1 September 2006 (UTC)

Expanding "Real analysis"

I've just made a trip through Google Book Search, and it appears that the treatment of 0.999… in real analysis textbooks is even more diverse than I thought. I'll be expanding the section, possibly adding a couple more subsections to clarify the differences; these will have the benefit that they will flow more naturally into the following section on rational numbers. One of them will take the sequence limit within the real numbers; I realize that we were trying to avoid such a limit and the associated infinity sign, but it's an important idea that gets referenced again and again. Also, some subsections will have to be renamed more precisely. Melchoir 18:22, 2 September 2006 (UTC)

Is This an Encyclopedia Article?

This article is quite interesting, but I'm not sure if it belongs in an encyclopedia instead of a journal of mathematics. I feel like an encyclopedia isn't really where I would look for a mathematical proof. It may just be the fact that I'm not a mathematics expert that makes me wonder. Perhaps this is a well-established, classical mathematical truth? If so, why is the extensive proving necessary? If it is an exploration, perhaps there is a better venue in which it ought to be published? Chadbald 05:44, 3 September 2006 (UTC)

Um... that's a lot of questions! I'd say that, yes, this is a classical mathematical truth, even more classical than some of the proofs! It isn't strictly necessary to prove it more than once, but it's one of those popular problems that has attracted lots of proofs anyway.
As for what this article is, well, it's currently undergoing several changes. I suspect that its broad structure isn't going to shift too much more, but one problem is that it doesn't have a lead section that provides an overview of the article. We'll write one soon.
I'm interested in learning this: what would you expect from an encyclopedia article on the topic? Melchoir 06:01, 3 September 2006 (UTC)
Thanks for your help. I think you're right, and a lead section would help immensely. Now that you mention it, I think it was the opening sentence that set me up to think of the whole article the wrong way. As it stands, it sounds a bit polemic, especially to a layman such as myself, as if the point of the article is to argue against the notion of .999... equaling "approximately" 1. From what you've told me, this is not the case.
I would also suggest one other small but significant change that would help someone like me understand what the point of the article is: Could we change the title to "Proofs that 999... equals 1"? I feel that simply making the title plural would immediately let a reader know that they are looking at classical and established processes and not "news." Do you see what i mean? Calling it "Proof that..." led me to expect the article to be establishing something new, just as a newspaper headline might read, "Proof That There Are Planets Outside Our Solar System." I could be totally offbase or maybe just nit-picky, but I feel like it would give the article the informational we're looking for instead of an argumentative feel.
But now that I better understand the purpose of the article, the content is exactly what I would expect. Someone curious about established proofs of this truth should have this resource available to them. Chadbald 05:59, 4 September 2006 (UTC)
Awesome! On the naming issue, my personal preference is simply "0.999…". The current title comes from early versions of the article that contained only a proof or proofs; it now contains much more material of general relevance to 0.999… from diverse approaches. (See, for example, the article one year ago. It favors a specific proof under the spartan heading "Proof", hence the singular, describing some others as alternatives. An earlier version contains just the one proof.) So I also see what you mean about "proofs", but plurals are a tricky issue on Wikipedia, and usually they're omitted from titles. See Wikipedia:Naming conventions (plurals). Another benefit of "0.999…", now that you mention it, is that it's the least argumentative of all.
I also sympathize about the opening sentence. The idea of approximate equality belongs in the "Skepticism" section, properly sourced of course, and in the lead section it should appear only alongside a statement about the frequent confusion surrounding 0.999…. You're welcome, of course, to edit the lead as you see fit! Melchoir 06:54, 4 September 2006 (UTC)
I would support a move to either 0.999… or Proofs that 0.999… = 1. I've never thought of it before, but now that Chadbald mentions it, the current title does have an ORish ring to it. I can understand exactly how it made him uncomfortable. -- Meni Rosenfeld (talk) 09:59, 4 September 2006 (UTC)
I also support moving the article to 0.999…, including a fair/balanced section on Skepticism for NPOV, and a lead section along the lines of "0.999... is a common representation of the decimal number between zero and one with an infinite number of nines after the decimal point. It can be proven that this number is, in fact, equal to one, a result which some/many people find counter-intuitive for a number of reasons." with, of course, appropriate sourcing for the various bits. Confusing Manifestation 10:26, 4 September 2006 (UTC)
I suggested 0.999… in an earlier thread and I still support that title. Fredrik Johansson 11:03, 4 September 2006 (UTC)
Haven't contributed anything in a while, but I also support a move. Give it a day or so, and if there aren't a plurality of objections, then I say Melchoir does the move. Also, since '…' is a Unicode character, there will have to be a redirect from 0.999.... On previewing, looks like there already is, made by Mets501. Supadawg (talk • contribs)
Hell no! Melchoir has trashed the article quite enough. We have a number of "Proof…" articles. This was a fine article, and will be again once I have the stomach to correct the damage that has been done to it. The "extensive proving" and out-of-control citing is absurd, as I pointed out when Melchoir started it, but my objection was taken as a signal to do even more. Previously there were exactly four proofs, each brief and each serving a different purpose. The history of Melchoir's opinions and "contributions" to this article has been one unmitigated disaster after another. It no longer benefits the audience that needs it. --KSmrqT 08:25, 5 September 2006 (UTC)
The following discussion is an archived debate of the proposal. Please do not modify it. Subsequent comments should be made in a new section on the talk page. No further edits should be made to this section.

The result of the debate was move. JPD (talk) 15:09, 14 September 2006 (UTC)

Requested move

Proof that 0.999... equals 1 → 0.999... – More accurate reflection of content; simpler; less argumentative. Melchoir 14:48, 5 September 2006 (UTC)

Survey

Add "* Support" or "* Oppose" followed by an optional one-sentence explanation, then sign your opinion with ~~~~

I don't see the problem. The notation "...999" is quite different from "0.999...". -- Meni Rosenfeld (talk) 19:30, 5 September 2006 (UTC)
See P-adic#Notation. — Arthur Rubin | (talk) 19:51, 5 September 2006 (UTC)
I gather from that link that p-adic expansions are sometimes written to the right? It would be confusing to adopt that notation, but I guess we could make a note in the relevant section. Melchoir 19:57, 5 September 2006 (UTC)
I've never seen it myself, but a reference was given (at least on the talk page, if not in the article — I haven't checked the P-adic article itself recently). — Arthur Rubin | (talk) 20:01, 5 September 2006 (UTC)
Melchoir was never the only one to dislike both the content and title. The nature of the topic of this article (the fact that so many people seem to think that 0.999... ≠ 1) means that an article with just a proof (or proofs) won't really benefit anyone (I have the impression that anyone with enough knowledge to understand the proofs originally presented, would also be able to derive them himself anyway). Any sensible article must discuss 0.999... within a broader context, and with a title to match. -- Meni Rosenfeld (talk) 08:31, 6 September 2006 (UTC)
All of the examples you gave, with the exception of the last, have corresponding articles about the general concept. For example, there is Proof of Bertrand's postulate and Bertrand's postulate. In my opinion, the article should be more general, giving historical context and analysis of skepticism over the equality to 1. This is already reflected in the body of the article, and the title should follow suit. If there is enough material, somewhere down the line the article could be split in two, with one devoted to proofs of the equality and the other devoted to everything else. This would follow the pattern of the articles you've cited.
Attacking Melchoir, instead of the issue itself, does nothing to help anyone's cause. I dislike the phrase "large-scale assault" and your implication that an editor in good standing requires supervision, especially when none have voiced opposition to his edits except you. Yes, some of his edits make the article more verbose, but how about editing it and working together to reach a compromise, instead of doing blanket reverts? Again, KSmrq, you stand alone in opposition. Please do not assume you have authority over the rest of the editors here. Supadawg (talk • contribs) 20:32, 6 September 2006 (UTC)
  • Conditional Oppose. In its present state the article is a proof that 0.999... = 1. As long as the 0.999... redirects here I see no proplem. IF the article becomes more general on the number 0.999..., as opposed to its current state as merely a set of proofs, then I will Support such a move. Maelin 14:54, 8 September 2006 (UTC)
    • Um... the whole second half of the article consists not of proofs that 0.999... = 1 but of Generalizations, Other number systems, Applications, and Skepticism. What do you think it's missing? Melchoir 16:34, 8 September 2006 (UTC)
  • I support this change. Peter O. (Talk) 06:21, 13 September 2006 (UTC)

Discussion

Add any additional comments

Other options

  • Following the example from KSmrq's list of articles named Proof..., could we have both: An article named Proof that 0.999... equals 1 (or should it be Proofs?), with the standard mathematical arguments, and another one named 0.999..., dealing - in an encyclopaedic way - with the misconceptions and folklore?--Niels Ø 08:18, 13 September 2006 (UTC)
Possible, but I think the proofs are neither hard nor interesting enough to merit their own article. With the proper setup, they're no more than trivial one-liners. -- Meni Rosenfeld (talk) 08:23, 13 September 2006 (UTC)
You may be right about that, but in cases like this one, it is not enough to aim at a correct and sensible exposition; we should also aim at something that will not be corrupted all the time - if it can be done without compromising the integrity of the articles. KSmrq seems to be arguing that we should only have an article with stuff that you say is without enough merit to have an article of its won. Having both articles, everyone (well, more of us, at least) can be reasonably happy, I think.--Niels Ø 08:35, 13 September 2006 (UTC)
I'm not sure I understand how having 2 articles will prevent them (or one of them) from being corrupted. Are you saying that people are less likely to insert nonsense into a proof article? That doesn't seem to agree with the history of this article. -- Meni Rosenfeld (talk) 08:43, 13 September 2006 (UTC)
I might support a variant of the idea: splitting off the sections detailing the mathematical development / proofs of 0.999… into a sub-article per Wikipedia:Summary style, and leaving behind a lighter summary here. This move might become necessary, as the article is getting long. In fact, I can even envision two more sub-articles: one on connections with other mathematics (generalizations, applications, other number systems) and one on conceptual difficulties alone. But these are big decisions, and I'd rather postpone them until all the content is laid out and we can do a Peer Review. Melchoir 17:11, 13 September 2006 (UTC)
The above discussion is preserved as an archive of the debate. Please do not modify it. Subsequent comments should be made in a new section on this talk page. No further edits should be made to this section.

Reverting

I thought we were over this. I'm anxious to get back to work on the article, and I'm confident that I can fix whatever problems are brought to my attention. Can I get a consensus here that this revert is inappropriate and counterproductive? Melchoir 16:10, 5 September 2006 (UTC)

OK, first replace all < div > headings by subsections. You seem to be be unWikifying the article. Then we can start discussing indivdual changes.
Second, I think User:The Anome's changes to the introduction are harmful. I prefer User:Melchoir's version of 08:48, September 5, 2006 , although the version (of 08:27) I reverted to is acceptable.
Third, both User:KSmrq and I have reverted your changes, pretty much for the same reasons. I don't see how you can say there is consensus that the reversions are inappropriate. — Arthur Rubin | (talk) 17:50, 5 September 2006 (UTC)
First: You could have just asked me. The div headings are only for backwards compatibility with incoming section links. They invisibly demarcate areas that are currently too short to necessitate or merit subsections of thier own.
Second: Thank you!
Third: Two editors with similar edit summaries do not make a consensus. Using a revert as an opportunity to vent frustration through the edit summary box is, in fact, actively harmful to the process of building consensus. There are many editors watching this article who would rather stay out of a revert war but who are often willing to provide their opinions on the talk page. Melchoir 18:03, 5 September 2006 (UTC)
...but of course it's infinitely better than being hit without explanation by popups. Surely no one will fault me for undoing this last? Melchoir 18:23, 5 September 2006 (UTC)
First; they look like subtitles, they should act like subtitles.
Third; neither does one (User:Melchoir). The other recent edits don't seem to agree with either group. 2 to 1 qualifies as a super-majority, if not a consensus. But, thinking about it, your proofs do seem better than the other version, for the most part. Perhaps I'll edit in some of the simpler versions, later.
And I haven't installed popups. My reversions were both manual edits, although without much explanation.
Further details; Game theory should probably be piped to specifically Conway-style games. (I don't remember where we put the article, although it's probably in my watch-list). Found it: combinatorial game theory.
Could you check the "Breaking subtraction" section again; I don't think that works correctly. But I don't have the reference available to check, unles it's online.
In the p-adics, the double-decimals DOES NOT WORK. Adding one of the four 10-adic to of the decimal doesn't "equate" to 0, even if …999.999… can equate to 0. I've looked at that one, so, even if the reference does state it can be done, it can only apply to "numbers" which can be equated to a rational number, i.e., if both sequences are periodic. This pretty much amounts to equating a rational p-adic with the rational real, which seems arbitrary. (Furthermore, if we go to the p-adics, we have to mention the left-to-right notation, as we've done so in that article.) — Arthur Rubin | (talk) 18:31, 5 September 2006 (UTC)
By "popups" I refer to this; presumably it happened while you were writing. Melchoir 18:35, 5 September 2006 (UTC)
For breaking subtraction, two links to the reference are in the References section, under "Richman". The free link is mostly the same. Melchoir 18:38, 5 September 2006 (UTC)
That was the other guy, but I can understand why you think we're the same person. Checking "breaking subtraction" references. For what it's worth, as I reverted one move and two of your edits/reversions, so I'm out of this for a while, under WP:3RR. — Arthur Rubin | (talk) 18:42, 5 September 2006 (UTC)
Okay. While you check out Richman, I'll paste in the quote from Rudin:
"20. With reference to the Appendix [on Dedekind cuts], suppose that the property (III) [no greatest element] were omitted from the definition of a cut. Keep the same definitions of order and addition. Show that the resulting ordered set has the least-upper-bound property, that addition satisfies axioms (A1) to (A4) [closure, commutativity, associativity, identity] (with a slightly different zero-element!) but that (A5) [inverses] fails."
Melchoir 19:35, 5 September 2006 (UTC)
OK, the "positive decimals" form a semiring under the appropriate definitions, and the cuts form an ordered groupoid, or something like that, and the reference seems to say that, as well. — Arthur Rubin | (talk) 19:48, 5 September 2006 (UTC)
Yeah, and there's more that Richman has to say about the relationship between the two structures, especially in relation to negatives. I figured that material would stray too far from the topic. Melchoir 20:12, 5 September 2006 (UTC)
I am well aware that double-decimals don't work in the p-adics. I did not claim that they did, nor did I write that they did in the article. Now, if I recall correctly, the reference requires only that the left end of the sequence is periodic. Either way, you are welcome to add a caveat to that effect. Melchoir 18:44, 5 September 2006 (UTC)
...or at least you'd be welcome if we were doing this the civilized way. KSmrq, could you please either join the discussion or undo your revert? I find it personally offensive. Melchoir 18:46, 5 September 2006 (UTC)
I agree about game theory. That wasn't my writing anyway, although it's a good suggestion for a topic, as Hackenstrings are the only known example of a number system where something like 0.999… is less than 1 due to infinitesimals. Melchoir 18:50, 5 September 2006 (UTC)
Let's agree that the wholesale revert, without reaching consensus, was inappropriate. Let us also agree that it doesn't really matter - the article is adequate in its current form, and reverting it back and forth won't help anything. Our energies should be focused on discussing the desired form of the article here. That said, I believe Melchoir's version is better, and any new problems it may have introduced should be dealt with on a case-by-case basis (as has been initiated above by Arthur and Melchoir). -- Meni Rosenfeld (talk) 19:39, 5 September 2006 (UTC)
I agree with Meni Rosenfeld, the revert was wrong in my opinion and I think Melchoir's version is much better (even if it does have some issues which need to be discussed ). —Mets501 (talk) 19:44, 5 September 2006 (UTC)
Without commenting on which version is better, I also agree that the wholesale reverting isn't helpful. There are multiple editors with 2 or 3 reverts on this article in the past couple of days. Given the long history here, perhaps mediation by a third party would be beneficial.--Trystan 06:46, 6 September 2006 (UTC)
Thanks for your ideas, everyone (especially those who complimented and started cleaning up my work)! My immediate concern, besides the desire to continue editing the article, is that with Chuayw2000's recent edits to KSmrq's version, a content fork has in some sense developed. We don't want to be working on two versions simultaneously. I guess the most neutral thing to do would be to protect the article, but I hope there's enough of a consensus here that we can agree to simply revert to 03:19, 6 September 2006 Supadawg instead...? Melchoir 16:50, 6 September 2006 (UTC)
(By the way, Chuayw2000 says he wouldn't be offended by a revert.) Melchoir 16:59, 6 September 2006 (UTC)

I've filed a request for protection (I can't do it myself because I'm involved). —Mets501 (talk) 18:47, 6 September 2006 (UTC)

Does this mean you want me to stop editing the article? Melchoir 19:11, 6 September 2006 (UTC)
...I guess I'll take that as a no. Back to work... Melchoir 21:44, 6 September 2006 (UTC)
Sorry, I should have been clearer. I prefer your version personally, so that's why I didn't protect it myself (not supposed to protect pages I'm involved with). Should I cancel the request now though, as KSmrq hasn't reverted again? —Mets501 (talk) 02:02, 7 September 2006 (UTC)
(Okay, I wanted to make sure that you didn't think I was aggravating the situation.) Maybe we should err on the side of reversible, light-handed solutions for the article. If you cancel the request, the worst that could happen is a few more reverts. Meanwhile, we'll have the opportunity to capitalize on recent participation and take the article down the home stretch to GA. Melchoir 02:17, 7 September 2006 (UTC)

Given the lack of discussion after 60 hours, I have listed this article for unprotection. Melchoir 17:26, 9 September 2006 (UTC)

Infinitesimals

Apparently A. H. Lightstone, a student and coauthor of Robinson, addressed decimals in NSA not long after the field was created. Lightstone's POV, contrary to this article's suggestion, is that decimals in NSA are (1) easy and (2) a useful educational device:

"The goal of this article is to enliven Abraham Robinson's concept of an infinitesimal by exhibiting infinitesimals in a simple and direct manner. ...To this end we shall exploit the familiar notion of the decimal expansion of a real number. After all, this notion improves our grasp of real numbers; just so, it will help us appreciate infinitesimals, indeed all numbers of our extended number system."

And that, kids, is why following references is better than doing original research. I was going to briefly expand on Hackenstrings next, but I think I'd better fix the overall readability first. Melchoir 17:10, 5 September 2006 (UTC)

Hey, hang on, Supadawg. Wikipedia:Lead section advises us that the lead section should summarize the entire article. Shouldn't it? Melchoir 23:28, 5 September 2006 (UTC)

Yes, it should summarize, but going into detail about how each proof is accomplished distracts the reader. Wikipedia:Lead Section says the summary should be concise, and I interpret that as telling the reader what will be done, not how; that's for the body of the article. The less fluff, the better. Supadawg (talk • contribs) 01:24, 6 September 2006 (UTC)
Well, that's reasonable. I could go either way on the sentence listing the methods; they're an important part of the article but maybe the reader doesn't care so early on. If you feel strongly about it, okay. But what about the former third paragraph on skepticism, popular discussion, and alternate number systems? Melchoir 01:50, 6 September 2006 (UTC)
Oh, I see where you're going now. The lead will still need something, though... hmm. Melchoir 01:53, 6 September 2006 (UTC)

As for first sentence's "the recurring decimal 0.999… (where the 9s recur)": surely there's a better, shorter way to say that? Melchoir 02:02, 6 September 2006 (UTC)

Possibly "the non-terminating decimal 0.999… (where the 9s recur)", or "the infinitely repeating decimal 0.999… (where the 9s recur)". Or maybe the "(where the 9s recur)" part isn't necessary; it's obvious by the notation. Supadawg (talk • contribs) 02:46, 6 September 2006 (UTC)
Yeah, I deleted it! So, you put it back by accident, then? Melchoir 03:01, 6 September 2006 (UTC)
*checks edit history* Yup, guess I did. Sorry about that; re-removing it now. Supadawg (talk • contribs) 03:18, 6 September 2006 (UTC)

Illustrations

Illustration that in base 3, 1 = 1.000… = 0.222… via nested intervals

While we wait for things to settle down, I'll work on some images. If anyone has feedback on the illustration to the right or suggestions for other illustrations, fire away. I have the Adobe Illustrator sources of course, so even the most minor changes are easy to implement. Melchoir 04:45, 7 September 2006 (UTC)

I'm unable to understand the image, but that may be because I'm unfamiliar with the area. Perhaps an explanation of how the image works? Supadawg (talk • contribs) 01:30, 8 September 2006 (UTC)
Ideally an illustration should be understandable without a long caption, but just so we're on the same page.... the horizontal line is the real number line, and visual elements are displaced above or below it only so that they can be told apart; the vertical scale is meaningless. The lower magenta rectangle depicts the part of the number line covered by [0, 1]; the cyan [.2, 1]; the yellow [.22, 1]; and the gray [.222, 1]. The upper segments and their rectangles are [1, 2], [1, 1.1], [1, 1.01], and [1, 1.001]. The green line shows how the number 1 is contained in all of the intervals, and therefore can be written either as 0.222… or 1.000…. The extra gray marks are unused subdivision points. The vertical gray line is 0.
Any ideas? Melchoir 01:57, 8 September 2006 (UTC)
Illustration that in base 3, 1 = 1.000… = 0.222… via nested intervals
Perhaps this is better? Melchoir 02:06, 8 September 2006 (UTC)
Yes, I see now. It's a great illustration of .222... approaching 1, but I don't see how it proves it, as the intervals could just as easily be [.2, 1), [.22, 1), and [.222, 1), which might actually seem more intuitive to someone who does not accept the theorem. Is there anything, in and of the illustration, that forces it to be closed on the right side? Supadawg (talk • contribs) 20:32, 8 September 2006 (UTC)
Well, it's hard to prove anything with an illustration. I tried to indicate closed intervals by capping them with square brackets and reducing the transparency of the rectangles' edges; perhaps the brackets and edges should be thicker and darker?
(As for half-open [)-type subdivisions, if one insists on them then 0.222… or 0.999… becomes undefined. And if you use (]-type subdivisions, 1.000… becomes undefined. Either style breaks equivalency with the supremum definition and prevents one from applying the Nested Intervals Theorem. I can probably dig up a source for either convention, and Apostol considers both in parallel. We could put a note, possibly towards the top of "Nested intervals and least upper bounds" since that's where it becomes most relevant, that some authors refuse to define or even consider 0.999…, but nonetheless whenever it is defined it equals 1.) Melchoir 21:14, 8 September 2006 (UTC)
Okay. I was just wondering if it was impossible to use half-open intervals, and it looks like it is. Thanks. Supadawg (talk • contribs) 22:04, 8 September 2006 (UTC)
Illustration that in base 3, 1 = 1.000… = 0.222… via nested intervals

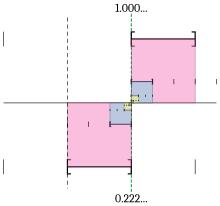
How's this? Melchoir 21:33, 8 September 2006 (UTC)

Looks good to me. Supadawg (talk • contribs) 22:04, 8 September 2006 (UTC)
  1. ^ Rudin pp.17-20
  2. ^ Rudin p.20 or Richman p.399. To be precise, Rudin and Richman would call this cut "1*" and "1−", respectively; both identify these with the traditional real number 1. Note that what Rudin calls a Dedekind cut, Richman calls a "nonprincipal Dedekind cut".
  3. ^ Richman p.399
  4. ^ "Mathematics Magazine:Guidelines for Authors". The Mathematical Association of America. Retrieved 2006-08-23.
  5. ^ Richman pp.398-399
Retrieved from "https://en.wikipedia.org/w/index.php?title=Talk:0.999.../Archive_9&oldid=1236227652"