Talk:Foucault pendulum vector diagrams
| This article is rated C-class on Wikipedia's content assessment scale. It is of interest to the following WikiProjects: | |||||||||||
| |||||||||||
[Untitled]
[edit]Some of the ideas for this article came from reading the book "Pendulum: Leon Foucault and the Triump of Science" by Amir D. Aczel, 2003. The diagrams were produced using a Visio program then imported as figures. The vectors that are shown are as close to scale as obtainable by the program and was helpful in evaluating the information in the diagrams. The words of the article are my own. I expect many comments and edits to improve the quality and for the ideas that were the inspiration for the article. Thanks in advance for any comments. First comment by David Harty 06:26, 8 January 2006 (UTC)
The plane of swing of the pendulum bob vs. spin of the pendulum bob
[edit]In the article it is stated:
- The swing of the pendulum establishes a vertical plane above the surface of the Earth that is independent of the rotation of the Earth.
What exactly is meant there? The direction of the plane of the oscillation is not always independent of the rotation of the Earth. If a Foucault pendulum is located on Earth, at 45 degrees latitude, then the rotation of the plane of oscillation will rotate in a ratio of 1:1.414 with the sidereal day of the Earth.
As you describe, in order to work correctly, the connection point of the wire must be such that it can rotate freely, otherwise a twist of the wire will build up. This means that averaged over time a torque is being exerted on the bob. The two forces that are being exerted are gravitation and the tension in the wire. Those two forces are not exactly aligned, hence there is a resultant force. When, on a rotating planet, the pendulum bob is swinging, there is a torque that alters the direction of the plane of rotation. Cleonis 23:23, 9 January 2006 (UTC)
- My thought is that the pendulum bob can twist on the end of a wire without affecting the plane of the pendulum swing, and twist in the opposite direction as the resistance to the strain in the wire dictates. The wire stores and releases energy in the form of twisting and untwisting and this is separate from the swing that is established by the pendulum. At the North Pole, one twist of the wire will occur in one day and this occurs whether the pendulum is swinging or not (in relation to a static pendulum bob in relation to the stars). The pendulum bob only spins as transmitted through the supported wire or as initially spinning. The longer the wire, the less the buildup of strain per unit length of wire. So the swing of the pendulum establishes a vertical plane above the surface of the Earth that is independent of the rotation of the Earth unless affected through the connection apparatus. The plane of the swing is independent but the spin of the bob due to the twisting of the wire is not unless a frictionless connection point is made (which I don't think exists).
- The pendulum Sine Law is different than the spin on the bob and has to do with the rotation of the Earth that is observable. There are no velocity vectors associated with the pendulum, they are associated with the spin of the Earth underneath the pendulum. David Harty 04:39, 10 January 2006 (UTC)
For myself, I use the following model. I take the wire to be perfectly rigid, and I take the connection between the bob and the wire to be perfectly rigid. What remains is that the connection 'at the top' must be free to allow the wire to pivot with respect to the mounting. I assume that it is possible to devise a connection that has so little friction that the error it introduces is less than 1 part in 100. If the connection at the top does not allow free pivoting I do not categorize the pendulum as a Foucault pendulum.
I propose to make a distinction between 'rotation of the bob' and 'precession of the plane of oscillation'. Take a polar Foucault pendulum. If it is released with insufficient care, the motion of the bob in space will be in the shape of an elongated ellipse, but the orientation that ellipse will not precess with respect to the stars. So if the bob is released with insufficient care, then the precession rate will be the same as when the oscillation of the bob is truly planar. Releasing the bob with insufficient care does not compromise the observation of the precession of the plane of oscillation.
A polar Foucault pendulum is the only pendulum where the resultant force acting on the bob (averaged over time) is free of torque, hence the polar pendulum does not precess with respect to the fixed stars. For a Foucault pendulum at intermediate latitude (anywhere between the poles and the equator) the resultant force (after averaging over time) exerts a torque on the pendulum bob, causing the plane of oscillation to precess with respect to the stars.Cleonis 11:23, 10 January 2006 (UTC)
- If a pendulum is hanging at the North Pole, before the bob is released the bob is stationary but is rotating (spinning) with the Earth. Once the bob is released it will continue to rotate (spin) unless one stops the rotation (spin) by forcing a spot on the side of the bob to always line up or point to one star. If the rotation of the bob is stopped then the connection wire will twist one turn every day unless there is a connection that is free to rotate (spin) (at either end of the wire or the support structure). If the bob at the North Pole is allowed to continue to rotate (spin) then it will and the wire won't twist one turn in one day.
- The description of the Foucault pendulum is not clear on the specific details of the connection to the support structure but it is obviously very important. Some descriptions do not mention a special connection, only that it is free to swing in any direction which is not the same thing as the support connection being free to rotate (spin).
- The swing of the pendulum is different then the rotation (spin) of the bob. This is what is meant by the statement, "The swing of the pendulum establishes a vertical plane above the surface of the Earth that is independent of the rotation of the Earth." At the equator, the pendulum is moving with the rotation of the Earth as is the support structure so one can't see the rotation of the Earth in relation to the pendulum. So the pendulum does depend on the location of the surface of the Earth where the initial conditions are established. If one could imagine a large pendulum structure that is mounted at the North Pole and free to rotate but has long arms that allows the pendulum to swing at the Equator then the Earth's surface would move underneath the pendulum. The Earth doesn't rotate under the pendulum swing like at the North Pole but the equatorial plane rotates perpendicular to the pendulum swing, if you see what I mean. This is a very large pendulum and an idealized situation.
- If a pendulum is hanging at the North Pole, before the bob is released the bob is stationary but is rotating with the Earth. Once the bob is released it will continue to rotate unless one stops the rotation by forcing a spot on the side of the bob to always line up or point to one star. David Harty 13:01, 10 January 2006 (UTC)
- There two types of motions that need to be addressed. One, the motion of the swing of the pendulum, and two, the motion of the rotating bob separate from the swing of the pendulum.
- If a pendulum is hanging at the North Pole, before the bob is released the bob is stationary but is rotating with the Earth. Once the bob is released it will continue to rotate unless one stops the rotation by forcing a spot on the side of the bob to always line up or point to one star. If the rotation of the bob is stopped then the connection wire will twist one turn every day unless there is a connection that is free to rotate (at either end of the wire or the support structure). If the bob at the North Pole is allowed to continue to rotate (spin), then it will, and the wire won't twist one turn in one day.
- A person standing on the North Pole rotates with the turning of the Earth. This is the same with a static pendulum. If a dot is placed on a static pendulum bob facing towards one star, that dot will rotate with the Earth, unless stopped and unless there is a connection that is free to rotate (per Newton's first law). If a pendulum swing at the pole is lined up with one star it will continue to swing in that plane unless affected by an outside force. The description of the Foucault pendulum is not clear on the specific details of the connection to the support structure but it is obviously very important. Some descriptions do not mention a special connection, only that it is free to swing in any direction which is not the same thing as the support connection being free to rotate. That is why an article on Foucault pendulum connections is suggested.David Harty 23:54, 10 January 2006 (UTC)
- Ah, I think I now see where I misread you. I apologize. There is a possible pivoting of the bob around its own axis, (spin) and there is the swinging motion. I had not appreciated before that for a polar Foucault pendulum, the spin of the pendulum bob is in sync with the rotation of the Earth, hence in the case of a polar pendulum the connection 'at the top' does actually not need freedom to swivel.
Cleonis 10:18, 11 January 2006 (UTC)
- I have rewritten the paragraph about the Foucault pendulum connections and hope that it is clearer and more precise in terminology. The paragraph was only intended to introduce a more detailed article on the connections for the pendulum. David Harty 14:28, 11 January 2006 (UTC)
It is strongly suggested that an article be written to explain how the connections of the pendulum are made and cite famous examples such as the Pantheon apparatus, the Lexington apparatus, and/or others and also discuss or diagram the Charron chuck and how it is used in the pendulum apparatus. David Harty 01:33, 11 January 2006 (UTC)
It might be helpful to explain some of the previous statements in pertaining to a swinging pendulum vs. pertaining to a rotating pendulum bob (that rotates even when at rest). Such as your previous comments pasted below; 1. "What remains is that the connection 'at the top' must be free to allow the wire to pivot with respect to the mounting. I assume that it is possible to devise a connection that has so little friction that the error it introduces is less than 1 part in 100. If the connection at the top does not allow free pivoting I do not categorize the pendulum as a Foucault pendulum." How is pivot being used? 2. "A polar Foucault pendulum is the only pendulum where the resultant force acting on the bob (averaged over time) is free of torque"
The problem with words like 'rotate' and 'turn' is that one has to specify around which axis that motion is. I think the following terminology is in accordance with general practice.
Spin Spin always refers to rotation of a solid object around its own center of mass. I propose to speak exclusively about 'spin of the bob'.
Pivot The verb 'to pivot' always refers to rotation around a vertical axis. 'to pivot has a flavor of a mechanical mounting with it, whereas 'spin' is more associated with free motion.
Precession of the Earth vs. 'Precession' of the Pendulum
[edit]- Precession is a characteristic of spinning objects such as a top, the Earth, and a spinning bicycle wheel. I didn't think that the swing of the Foucault pendulum was considered a spinning object but maybe some initial conditions are imparted to the swing. I thought the observed rotation of the Earth underneath the swing was related to the degree of alignment with the axis of rotation of the Earth and not due to precession. David Harty 13:01, 10 January 2006 (UTC)
Precession That word is most often used for a particular motion of spinning tops and gyroscopes, but it is convenient to also use it in the context of the Foucault pendulum. When a gyroscope is precessing, then Precession is much slower than its spin. By analogy, a full rotation of the plane of swinging of a pendulum takes much more time that a single back-and-forth swing. There are parallels in the forces involved. It is general practice to refer to the rotation of the plane of swinging as 'the precession of the pendulum'.
Let a Foucault pendulum be situated at 30 degrees latitude. Let the plane of swinging start in latitudinal direction. The plane of swinging will precess from latitudinal to longitudinal and so forth.
The rate of the precession depends on the latitude and on the rotation rate of the planet that the pendulum is situated on. A Foucault pendulum situated on Earth at 30 degrees latitude will precess through a full circle in two sidereal Earth days. A Foucault pendulum situated on Mars at 30 degrees latitude will precess through a full circle in two sidereal Martian days.
Figuring out the Foucault pendulum will swing at the poles and at the equator is relatively straightforward. The interesting part is what happens at intermediate latitudes. Cleonis 15:20, 11 January 2006 (UTC)
What matters is the line of intersection of the plane of swinging and the plane of the Equator. In the case of a polar pendulum that line keeps pointing in the same direction. On all other latitudes that line of intersection rotates. --Cleonis 15:33, 11 January 2006 (UTC)
- Some questions to consider.
- Would an equivalent statement be, what matters is the degree of alignment of the central axis of the pendulum with the axis of the Earth? The degree of alignment is 100% at the poles (sine of 90 degrees latitude is 1, and is 0% at the equator (sine of 0 degrees latitude is 0).
- The line of intersection that I describe is intended as an aid in visualising. As you point out, for assessing the forces that are at play the alignment is the key factor.
- Would it be correct to state that the Earth is rotating underneath the pendulum rather than "rotation of the plane of swinging of a pendulum"?
- The case of 'the earth is rotating underneath the pendulum' applies exclusively for a polar pendulum. On other latitudes the plane of swinging of the pendulum does not keep pointing in the same direction with respect to the stars. This is why it is helpful to consider the line of intersection of the plane of swinging with the plane of the equator.
- With the analogy mentioned above would one say that precession occurs the most where the "rotation of the plane of swinging of a pendulum" is the fastest (at the pole where the swing doesn't rotate with respect to the stars) and that precession occurs the least where the "rotation of the plane of swinging of a pendulum" is the slowest (at the equator where the swing has the most movement with respect to the stars)? David Harty 11:16, 13 January 2006 (UTC)
- The manifestation of the Coriolis Effect is that the effect is greatest at the poles where the surface of the Earth is at right angles to the axis of rotation. The Coriolis effect decreases nearer the equator because the surface of the Earth is parallel to the axis of rotation. "Precession" is a rather misleading term to use and is not used in the normal sense of the word.David Harty 14:40, 22 January 2006 (UTC)
- A polar pendulum does not precess with respect to the stars; in the case of a polar pendulum the plane of swinging is not affected by the Earth. (A terrestrial polar pendulum and a Martian polar pendulum would not precess with respect to each other)
- I think it is better to define the precession of the plane of swinging as the precession with respect to the stars. Thus defined the precession is zero at the poles, and the closer to the equator, the more the precession rate with respect to the stars approaches one Earth day. --Cleonis | Talk 14:59, 13 January 2006 (UTC)
- Would an equivalent statement be, what matters is the line of intersection of the plane of the pendulum swing with the plane of the projected surface of the Earth underneath the pendulum swing. This is what is shown in the diagrams of the article as an aid to visualizing. David Harty 05:13, 14 January 2006 (UTC)
- You mention 'the plane of the projected surface of the earth underneath the pendulum swing' Projected onto what surface? Anyway, I think projective geometry is not the answer.
Cleonis 00:14, 15 January 2006 (UTC)
The plane of the pendulum swing turns with respect to the surface of the Earth. David Harty 01:50, 16 January 2006 (UTC) Or, from the other perspective, the surface of the Earth turns with respect to the plane of th pendulum swing.
An equatorial pendulum has a counterclockwise precession (as seen from the North pole). An equatorial pendulum has a counterclockwise precession with respect to the stars because the Earth is in counterclockwise rotation with respect to the stars (as seen from the North pole).
A Foucault pendulum is set up in such a way that it won't swing out far. So when a Foucault pendulum is situated at, say, 80 degrees latitude (just 10 degrees latitude away from the pole) then the point of suspension is at all times further away from the Earth's axis than the bob ever comes. So even that close to the pole one has reason to expect that the plane of swinging will precess counterclocwise with respect to the stars, in synchrony with the rotation of the Earth.
What actually happens at, say, 80 degrees latitude, is that instead of precessing counterclocwise with respect to the stars at a rate of 360° per day, the pendulum precesses only slowly with respect to the stars, precessing counterclockwise. A second mechanism (and making a diagram for that one is on my 'to do' list) is imparting a clockwise precession. That second mechanism is strongest when the wire is parallel to the Earth's axis. The further away from the pole, the less that alignment.
So at 30 degrees latitude the first mechanism imparts a counterclockwise precession of 360° per day with respect to the stars, and the second mechanism imparts a clockwise precession of 180° per day with respect to the stars. The resultant precession with respect to the stars is 180° counterclockwise per day. Onlookers on Earth see the pendulum precess with respect to the floor: 180° per day, clockwise.
As seen from a deeper level of analysis, the word precession is actually appropriate.
I have performed three Google searches:
"precession of the Foucault pendulum"
I used the above expression and Google returned 104 locations with exactly that phrase
Next I did a wide Google search: all pages with both the word 'precession' and the expression "Foucault pendulum", and Google returned 700 locations.
Finally I narrowed that search down again: all pages with both the word 'precession' and the expression "Foucault pendulum" and the URL ending in .edu
To that search Google returned 168 locations
I hope this will help in convincing you that in technical discussions of the Foucault pendulum it is general practice to refer to 'the precession of the Foucault pendulum'.
It can be demonstrated that the mechanics involved in the precession of a spinning top is related to the coriolis effect. However, I should not expect you to just take my word for that.
I can only submit that the Google search confirms that it is general practice in technical discussions to refer to 'the precession of the Foucault pendulum'. --Cleonis | Talk 20:29, 22 January 2006 (UTC)
- It seems to me that a precise understanding of terminology is needed in order to gain a full understanding of the observations. Often times, it seems that the terminology seems to be used or interpreted with different meanings of the word. David Harty 22:44, 22 January 2006 (UTC)
- A google search of the word 'precession' returns 1,890,000 locations. Only a very small fraction of these deal with the motion of a pendulum. The motion of a pendulum in relation to the surface of the Earth has different characteristics compared to the precession of a rotating object such as the Earth. It would seem that better (different) terminology could be applied to the motion of the pendulum swing in relation to the surface of the Earth. The "precession of the Earth" does not have an equivalent change in relative motion like the Pendulum Sine Law for the motion of the pendulum swing. It makes no sense to discuss a "Sine Law" for a change in "precession of the Earth" in the same manner that the Pendulum Sine Law describes the change in relative motion of the pendulum swing as a function of latitude. David Harty 21:33, 5 February 2006 (UTC)
Because the precession of the Earth is on such a vastly slower time scale, there is no influence of the precession of the Earth on the precession of the pendulum. From a theoretical point of view there is a certain similarity in that the mechanisms involved are related in the type of mechanism. But the precession of the Earth plays no part in the precession of the Foucault pendulum.
Any large celestial body that rotates will bulge at the equator, and that assymmetry away from a perfect sphere plays a part in the cause of precession of a celestial body. Cleonis 09:39, 24 January 2006 (UTC)
Anders Persson and Norman Phillips
[edit]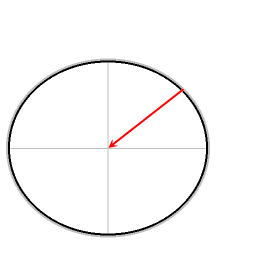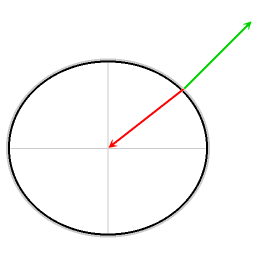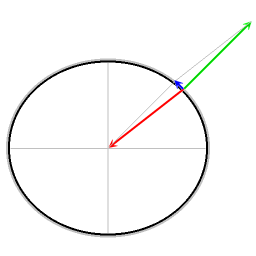
In my searches on information about the Foucault pendulum, I have come across two authors who correctly identify the force that is involved in causing the pendulum to precess with respect to the stars. One is the meteorologist Anders Persson, the other is also a meterolologist: Norman A Phillips.
Norman Philllips has written an article that is dedicated to discussing the Foucault pendulum. it is titled: What Makes the Foucault Pendulum Move Among the Stars. The english version of this article is not publicly available on the internet (It can be purchased)
I did find a note on the Foucault pendulum, written by Norman Phillips.
A french version of his article is publicly available Ce qui fait tourner le pendule de Foucault par rapport aux étoiles
A key element in understanding the motion of the Foucault pendulum is displayed in the diagram. If the resultant force that is depicted with the blue arrow is not taken into account, then the precession of the Foucault pendulum at latitides other than the poles is inexplicable. --Cleonis | Talk 07:51, 23 January 2006 (UTC)
Also see the Coriolis Effect article in Wikipedia and the discussion therein of "Visualization of the Coriolis Effect" and "Inertial Circles". David Harty 21:38, 5 February 2006 (UTC)
- The force indicated with the "blue arrow" is not the cause of the motion of the pendulum. It is due to the effect of the centrifugal force. If taken into consideration, it will cause a very small correction to the sin(lambda) law of the Foucault Pendulum. The linked articles get this wrong too (probably best to rely on physicist for this kind of analysis). —The preceding unsigned comment was added by 70.224.84.113 (talk) 15:35, 16 December 2006 (UTC).
What if the Earth was a Right Cylinder?
[edit]What observations would be made for a Foucault pendulum mounted at 45 degrees if the Earth was a right cylinder? In this case the Earth has the diameter equal to that at the equator and a cylindrical length from the North to South poles with the N-S axis of rotation running down the center of the length of the cylinder. The pendulum is mounted on the edge where the side of the cylinder meets the circular 'top' of the cylinder so the center-line of the pendulum (always directed to the center of gravity of the Earth) is at 45 degrees to the axis of rotation. Along the cylindrical sides of the 'cylinder-Earth' the surface velocity is all the same (equal to that of the equator). Since there is no change in surface velocity along the length of the cylinder, there is no Coriolis Effect which is the point of the question. The change in surface velocity is 'compressed' to the 'top' surface of the cylinder which corresponds to 45 degrees 'latitude' to the pole 'latitude'. Aside from totally messing up the weather since the cylindrical side from 45N to 45S would have the same solar alignment as the Equator and there is no Coriolis Effect in that range to create storms, how would the pendulum respond mounted at 45 degrees? Here are some multiple choice answers to the question but there can only be one correct response.
- a) It still takes 1.414 days to observe the rotation of the surface of the cylinder-Earth in relation to the pendulum swing because the alignment of the center-line of the pendulum is 45 degrees to the axis of rotation of the cylinder-Earth.
- b) The rotation of the cylinder-Earth will not be observable in relation to the pendulum swing because there is no Coriolis Effect at this point so the pendulum observation is like it would be at the Equator of the real Earth.
- c) It would take 1 day to observe the rotation of the surface of the cylinder-Earth in relation to the pendulum swing because the surface of the cylinder-Earth at this point is at right angles to the axis of rotation of the cylinder-Earth.
- d) None of the above.
- The correct answer is b), ... I think. David Harty 02:48, 24 January 2006 (UTC)
- A body of mass as large as the Earth cannot be cilindrical in shape. Inexorably the force of gravity will pull it into a sphere, and if the body of mass is rotating (spinning) then gravity will pull it into an oblate spheroid.
- Maybe it is possible to chip away at an asteroid with a diameter of say, a kilometer, and there gravity is so small, the asteroid may retain its cilindrical shape.
- Oh, my conclusion is that it is answer a) It is the alignment of forces that counts. The normal force is provided by the tension of the wire, and there is the force of gravity. Those two are not aligned, and that is a key factor. Combined with the swinging of the pendulum you get the rotation of the plane of swinging of the pendulum, that takes 1.414 days at 45° latitude. Cleonis 09:24, 24 January 2006 (UTC)
- The force of gravity changes as a function of R squared so the answer is probably d) none of the above. Trying to illustrate a simple point turns out to be not so simple.David Harty 21:33, 5 February 2006 (UTC)
- If the alignment of the center-line of the pendulum to the axis of rotation of the cylinder-Earth is the key factor then the answer is a) as indicated in the article.David Harty 10:54, 22 March 2006 (UTC)
Coriolis effect (in meteorology), Eötvös effect, and Foucault pendulum
[edit]- It might be worthwhile to identify the Coriolis force related to the observed motion of the Foucault pendulum. There is a simple difference in the forces acting on a pendulum bob before it is released compared to after it is released. This is why there is a change in the motion of the pendulum swing in relation to the surface of the Earth and why there is a change in effect with latitude. If this is elucidating to the discussion of the Coriolis force it might be identified in the article. The Foucault pendulum also has important historical significance. The magnitude of the effect is related to the degree of alignment of the central axis of the pendulum to the Earth's axis of rotation.David Harty 12:11, 7 April 2006 (UTC)
At 45 degrees latitude, the Coriolis effect (as taken into account in meteorology) and the Eötvös effect are equal in magnitude. (Sine and cosine of 45 degrees)
In the Eötvös effect article I used the example of the amount of buoyant force that a zeppelin needs to maintain height above the surface of the Earth. When a fast-moving zeppelin makes a U-turn, going from eastward to westward motion (with respect to the Earth), it must retrim its buoyancy.
During eastward travel the zeppelin will tend to veer to the south equator, during westward travel the zeppelin will tend to veer to the nearest pole. The Coriolis effect (as taken into account in meteorology) and the Eötvös effect are perpendicular components of one and the same effect, that is why they both have the same dependency on velocity with respect to the Earth, with that typical factor 2.
Thís mechanism also explains the precession of the plane of swing of a Foucault pendulum. The trajectory of the pendulum bob is not a ballistic trajectory, for the pendulum bob is suspended. Let a Foucault pendulum be located at 45 degress latitude. When the pendulum bob swings in eastward direction, it veers towards the south equator, on the opposite swing, to the west, it veers to the nearest pole. That is part of the mechanism that makes a Foucault pendulum precess though an entire circle. For a Foucault pendulum located at 45 30 degrees latitude, precessing through an entire circle takes 2 sidereal days, and the rate of precession is fairly constant throughout. --Cleonis | Talk 14:47, 8 April 2006 (UTC)
- It is not clear that the Eotvos effect is the correct term to use in discussion of the motion of the pendulum bob in relation to the surface of the Earth. The Eotvos effect (per the definitions) is a vertical deflection that changes the gravity and with it the weight of the body for an object that is moving. It is not clear that this effect is what causes the motion of the pendulum bob to change with respect to the surface of the Earth (as compared to a change in the vertical or gravitational force or buoyancy force). There is a 3-dimensional deflection system for which the Coriolis effect is only one part and the Eotvos effect is one part. In many articles and books there is an inconsistency in the usage of the 3-dimensional gyroscopic terms and attributions to the Coriolis effect as well as the commonly known ballistic effects. These 3-dimensional gyroscopic terms are being clarified in this discussion and Coriolis effect article. The point of connection of the pendulum bob is not moving with respect to the surface of the Earth and forces acting on the pendulum bob are acting through the point of connection of the pendulum apparatus. Since the point of connection is not moving with respect to the surface of the Earth it is not clear that the Eotvos effect is applicable to the observed change in motion of the Foucault pendulum. David Harty 10:40, 10 April 2006 (UTC)
- It is not clear that the Eotvos effect is the correct term to use in discussion of the motion of the pendulum bob in relation to the surface of the Earth.. In fact, it is readily apparent that the Eotvos effect is not the correct term to use in discussion of the motion of the pendulum bob in relation to the surface of the Earth. Foucault's pendulum will work beautifully at the poles (with period 24 hours), where the Eotvos effect vanishes, and the Coriolis effect doesn't... -- GWO
- It appears to me that the point of the Anders Perssons article is to describe all of the three dimensional deflective mechanisms in a rotating system. The title becomes somewhat misleading since the paper deals with the 3-dimensional system not just the Coriolis Effect. He describes horizontal deflection of vertical motion, vertical deflection of horizontal motion (Eotvos Effect), and the horizontal deflection of horizontal motion of which there are two parts which he calls the common centrifugal force and the compound centrifugal force (the Coriolis Force. These deflective mechanisms are apparently all present together because they are all part of the rotating system. The purpose for bringing up the Foucault pendulum is that it may isolate certain forces and be helpful in defining which forces cause the observed period of rotation of the pendulum. It seems that the force which determines the rotation is horizontal deflection of horizontal motion (Coriolis force) and the vertical deflection of horizontal motion (Eotvos) is not contributing to the observed period of rotation. If the pendulum wire were a spring rather than a ridgid wire would the bob move up and down due to the Eotvos Effect? David Harty 16:10, 12 April 2006 (UTC)
- It is not clear that the Eotvos effect is the correct term to use in discussion of the motion of the pendulum bob in relation to the surface of the Earth. The Eotvos effect (per the definitions) is a vertical deflection that changes the gravity and with it the weight of the body for an object that is moving. It is not clear that this effect is what causes the motion of the pendulum bob to change with respect to the surface of the Earth (as compared to a change in the vertical or gravitational force or buoyancy force). There is a 3-dimensional deflection system for which the Coriolis effect is only one part and the Eotvos effect is one part. In many articles and books there is an inconsistency in the usage of the 3-dimensional gyroscopic terms and attributions to the Coriolis effect as well as the commonly known ballistic effects. These 3-dimensional gyroscopic terms are being clarified in this discussion and Coriolis effect article. The point of connection of the pendulum bob is not moving with respect to the surface of the Earth and forces acting on the pendulum bob are acting through the point of connection of the pendulum apparatus. Since the point of connection is not moving with respect to the surface of the Earth it is not clear that the Eotvos effect is applicable to the observed change in motion of the Foucault pendulum. David Harty 10:40, 10 April 2006 (UTC)
Foucault pendulum bob suspended on a spring (instead of on a wire)
[edit]I copy and paste from above:
If the pendulum wire were a spring rather than a ridgid wire would the bob move up and down due to the Eotvos Effect? David Harty 16:10, 12 April 2006 (UTC)
Eötvös designed this impressively small instrument that demonstrates the Eötvos effect.
In the case of a pendulum-like device, the Eötvös effect will be visible most clearly under the following circumstances: Let a pendulum have a period of swing of, say, 10 seconds. Let the elasticity of the wire/spring be such that the natural period of bobbing up and down of that "pendulum" is the same 10 seconds.
Let that pendulum start swinging in east-west direction, initially without up-down motion. During each individual swing the Eötvös effect will be very small, but over a number of swings contraction and elongation of the spring will accumulate. --Cleonis | Talk 10:28, 18 April 2006 (UTC)
delete
wrong diagram
[edit]moved from Talk:Main Page Nil Einne 20:55, 3 May 2007 (UTC)
the topic: "foucault pendulum vector diagram" has a fault in one of the figures.. The middle diagram of the figure: "2B - Equatorial Pendulum Latitudinal Swing" has some earth velocity vectors added, moving to anticlockvise, eventhough the diagram clearly shows that the earth are mocing clockvise (a round arrow over the middle(North)).. Somone should change the direction of the velocity vectors going around.. Hope this was the right place to write this..¨ //thomasnielsen 16:24 3maj 2007
- Errr... I have no idea what you're talking about, but if it's about a specific article, ask on that article's talk page. This talk page is for discussion of the Main Page. —Cuiviénen 15:24, 3 May 2007 (UTC)
propose merge into Foucault Pendulum
[edit]Why shouldn't we merge this into Foucault Pendulum? RJFJR (talk) 14:36, 29 May 2009 (UTC)
- I'd be against merging them simply because this article is positively enormous in comparison; I think it would drown out the original article's content. What are your thoughts? Somnambulent (talk) 16:51, 29 November 2010 (UTC)
Does this article assume fixed wire or a wire hanging from a swivel?
[edit]Is the reason that there is a movement of the pendulum's plane relative to distant stars when it is located at the North Pole that there uis a small torque from the rotation of the fixed point (i.e pixed point is held by the spinning Earth and twists relative to the hanging weight)? Has anyone ever set-up a Foucault pendulum at the North Pole with a diamond point on a diamond plane swivel point to measure if the plane of the pendulum motion says fixed to a distant galaxy/star? D c weber (talk) 16:46, 20 December 2012 (UTC)
Original research?
[edit]Given the oldest comment (i.e. the one by @David Harty in 2006) and the lack of distinct sources, I assume that this page (mostly) consists of original research. Since this was first written, have any of these examples and derivations made it into published sources that we could reference? BalinKingOfMoria (talk) 02:15, 19 January 2023 (UTC)
- This is 99.99% original research. It belongs on some blog, unless wikiproject history of science wants to take it. 67.198.37.16 (talk) 03:12, 16 May 2024 (UTC)

