Talk:Hyperbolic geometry
| This is the talk page for discussing improvements to the Hyperbolic geometry article. This is not a forum for general discussion of the article's subject. |
Article policies
|
| Archives: 1, 2Auto-archiving period: 365 days |
| This It is of interest to multiple WikiProjects. | ||||||||||||||||||||||||
| ||||||||||||||||||||||||
The saddle diagram is inappropriate
[edit]While it is true that surfaces of negative curvature have a saddle-like appearance, it is known that the only Euclidean 2-dimensional surface of constant negative curvature is the pseudo-sphere which looks quite unlike the diagram shown. As far as I can see, the pseudo-sphere is not mentioned in the article although it has some historical importance. JFB80 (talk) 11:01, 5 December 2018 (UTC)
- @JFB80:Not just the pseudo-sphere. See the section "Surfaces of constant curvature" at http://roguetemple.com/z/hyper/models.php.TheKing44 (talk) 14:00, 5 December 2018 (UTC)
- To JFB80: If the surface is finite in extent, having a boundary, then it does not have to be the pseudo-sphere. If you disagree, please provide a citation or a proof. JRSpriggs (talk) 21:29, 5 December 2018 (UTC)
- To TheKing44: All these are models. Yes we all know models exist. What I mean is a surface in Euclidean space which is a hyperbolic space.
- To JRSpriggs: The usual case is for infinite space and this is what is normally understood. Is there any mention of special finite Euclidean constructions in the article?. But anyway why are you so much against mentioning the pseudo-sphere? As I said it has historical importance. JFB80 (talk) 17:23, 6 December 2018 (UTC)
- To JFB80: I am not opposed to mentioning the pseudosphere and, in fact, it is already mentioned several times in the article. I just disagreed with your statement about it being the only way to embed a hyperbolic 2-space into an Euclidean 3-space. Although now, I am not so sure that you were wrong. Also a small part of the pseudosphere might well look like that diagram. JRSpriggs (talk) 22:36, 6 December 2018 (UTC)
"Universal hyperbolic geometry" listed at Redirects for discussion
[edit]
An editor has asked for a discussion to address the redirect Universal hyperbolic geometry. Please participate in the redirect discussion if you wish to do so. –Deacon Vorbis (carbon • videos) 14:26, 1 February 2020 (UTC)
Geodesics in the hemisphere model
[edit]@Lethe: @David Eppstein: Regarding the section Hyperbolic geometry#The hemisphere model. Lethe described the geodesics in the hemisphere model as "semicircles orthogonal to boundary". I reverted him saying "some are, but some are not.". Then David Eppstein reverted me with the challenge "Describe one that is not.".
Any semicircle in the hemisphere which is orthogonal to the boundary must either pass through the point (0, 0, +1) or be the intersection of hemisphere with a vertical plane which does not pass through (0. 0. 0). Any geodesic in the hemisphere must be the intersection of the hemisphere with a plane which does pass through (0, 0, 0). For example, the plane y = z. It will meet the boundary at a 45 degree angle (i.e. not orthogonal). JRSpriggs (talk) 03:04, 3 October 2020 (UTC)
- You are thinking of geodesics for the spherical geometry on the hemisphere, I think? It is a different geometry than the one described here and has different geodesics. Another way to think of the hemisphere model of hyperbolic geometry: take the Klein model (a disk or ball in Euclidean space in which the hyperbolic geodesics are represented as Euclidean straight line segments), think of this disk or ball as being the projection of a higher-dimensional Euclidean sphere, and lift the line segments vertically onto the upper hemisphere. The resulting representations of hyperbolic geodesics on the hemisphere are always the intersections of the hemisphere with vertical planes, producing exactly semicircles perpendicular to the boundary. —David Eppstein (talk) 07:09, 3 October 2020 (UTC)
- To David Eppstein: Thank you for clarifying that and correcting my mistake. JRSpriggs (talk) 00:07, 5 October 2020 (UTC)
comparison_of_geometries.svg
[edit]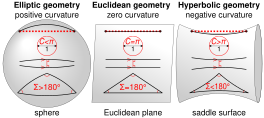
Hi @JRSpriggs:, thanks for your reversion pointing out my previous swapped curvature signs. Could you please detail how this diagram can be improved to your satisfaction? Cheers, cmɢʟee⎆τaʟκ 10:45, 8 October 2020 (UTC)
- It is fine now that you corrected the signs of the curvature. JRSpriggs (talk) 21:14, 8 October 2020 (UTC)
- Thanks, JRSpriggs. Much appreciated, cmɢʟee⎆τaʟκ 18:58, 9 October 2020 (UTC)
Lobachesky
[edit]@JRSpriggs: removed the note that the mention of russian mathematician-plagiarist has more to do with Soviet Cold War propaganda than historical facts. This name is not used in any serious English-language source, in extreme cases it is mentioned as an alternative with a reference to the Iron Curtain. I think it is necessary to return this comment or completely remove inappropriate references to this mathematician. When I studied the topic of non-Euclidean spaces at the university (including the history of this branch of mathematics), I never heard that name. I think that says a lot. Attempts to turn Wikipedia into a stronghold of communist propaganda should not be allowed. 217.19.208.109 (talk) 15:27, 8 July 2021 (UTC)
- I'm curious about which book would talk about the "history of this branch of mathematics" and not mention Lobachevsky, do you have any available references? Cheers, jraimbau (talk) 11:15, 9 July 2021 (UTC)
- If there are any mentions, it happens only in the context of describing the propaganda by russians/communists, who in every field of science tried to come up with their own "discoverers". This is wildness and cannot be seriously mentioned on Wikipedia outside of the section on historical absurdities. There was a feeling that an article on such a neutral topic was written by absolutely biased editors, promoting their POV. 217.19.208.109 (talk) 18:18, 9 July 2021 (UTC)
- This is just nonsense I'm not going to answer. I'm still curious about a reference on the history of geometry that doe not mention Lobachevsky in relation with hyperbolic geometry or that substitutes your wild claims, let me know if you find or recall one. Cheers, jraimbau (talk) 21:51, 9 July 2021 (UTC)
- I assumed that this conversation would boil down to insults. I am 67 years old, and I will not allow myself to be treated like that! I have been using Wikipedia for over a dozen years, but I have never seen anyone allow the communists to promote their ideology here. Are you russian or do you work for them? 217.19.208.109 (talk) 00:36, 11 July 2021 (UTC)
- You do know that when Lehrer used Lobachevksy's name in the song Lobachevsky (song), it was purely because it had the right number of syllables, and not because of any actual history, right? There is no serious dispute that Lobachevksy should be listed with Gauss and Bolyai as one of the founders of hyperbolic geometry, and the first to publish of the three. —David Eppstein (talk) 02:02, 11 July 2021 (UTC)
- I assumed that this conversation would boil down to insults. I am 67 years old, and I will not allow myself to be treated like that! I have been using Wikipedia for over a dozen years, but I have never seen anyone allow the communists to promote their ideology here. Are you russian or do you work for them? 217.19.208.109 (talk) 00:36, 11 July 2021 (UTC)
- I know I'm late to this discussion, but thanks a lot for a good laugh. –jacobolus (t) 04:30, 9 January 2024 (UTC)
- C-Class vital articles
- Wikipedia level-5 vital articles
- Wikipedia vital articles in Mathematics
- C-Class level-5 vital articles
- Wikipedia level-5 vital articles in Mathematics
- C-Class vital articles in Mathematics
- C-Class mathematics articles
- High-priority mathematics articles
- C-Class Russia articles
- High-importance Russia articles
- High-importance C-Class Russia articles
- C-Class Russia (science and education) articles
- Science and education in Russia task force articles
- WikiProject Russia articles



