Jump to content

Tiny Encryption Algorithm

From Wikipedia, the free encyclopedia

This is an old revision of this page, as edited by Itamarcu (talk | contribs) at 12:22, 30 May 2019 (Add link to Nothing-up-my-sleeve numbers). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

TEA
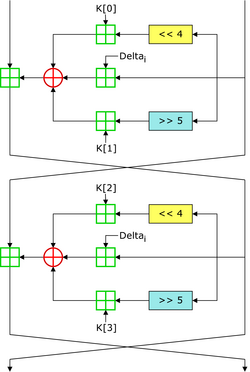Two Feistel rounds (one cycle) of TEA[1]
General
DesignersRoger Needham, David Wheeler
First published1994
SuccessorsXTEA
Cipher detail
Key sizes128 bits
Block sizes64 bits
StructureFeistel network
Roundsvariable; recommended 64 Feistel rounds (32 cycles)
Best public cryptanalysis
TEA suffers from equivalent keys (see text; Kelsey et al., 1996) and can be broken using a related-key attack requiring 223 chosen plaintexts and a time complexity of 232.[2] The best structural cryptanalysis of TEA in the standard single secret key setting is the zero-correlation cryptanalysis breaking 21 rounds in 2121.5 time with less than the full code book [3]

In cryptography, the Tiny Encryption Algorithm (TEA) is a block cipher notable for its simplicity of description and implementation, typically a few lines of code. It was designed by David Wheeler and Roger Needham of the Cambridge Computer Laboratory; it was first presented at the Fast Software Encryption workshop in Leuven in 1994, and first published in the proceedings of that workshop.[4]

The cipher is not subject to any patents.

Properties

TEA operates on two 32-bit unsigned integers (could be derived from a 64-bit data block) and uses a 128-bit key. It has a Feistel structure with a suggested 64 rounds, typically implemented in pairs termed cycles. It has an extremely simple key schedule, mixing all of the key material in exactly the same way for each cycle. Different multiples of a magic constant are used to prevent simple attacks based on the symmetry of the rounds. The magic constant, 2654435769 or 0x9E3779B9 is chosen to be ⌊232/ϕ⌋, where ϕ is the golden ratio (as a Nothing-up-my-sleeve number).[4]

TEA has a few weaknesses. Most notably, it suffers from equivalent keys—each key is equivalent to three others, which means that the effective key size is only 126 bits.[5] As a result, TEA is especially bad as a cryptographic hash function. This weakness led to a method for hacking Microsoft's Xbox game console, where the cipher was used as a hash function.[6] TEA is also susceptible to a related-key attack which requires 223 chosen plaintexts under a related-key pair, with 232 time complexity.[2] Because of these weaknesses, the XTEA cipher was designed.

Versions

The first published version of TEA was supplemented by a second version that incorporated extensions to make it more secure. Block TEA (which was specified along with XTEA) operates on arbitrary-size blocks in place of the 64-bit blocks of the original.

A third version (XXTEA), published in 1998, described further improvements for enhancing the security of the Block TEA algorithm.

Reference code

Following is an adaptation of the reference encryption and decryption routines in C, released into the public domain by David Wheeler and Roger Needham:[4] 

#include <stdint.h>

void encrypt (uint32_t v[2], uint32_t k[4]) {
    uint32_t v0=v[0], v1=v[1], sum=0, i;           /* set up */
    uint32_t delta=0x9E3779B9;                     /* a key schedule constant */
    uint32_t k0=k[0], k1=k[1], k2=k[2], k3=k[3];   /* cache key */
    for (i=0; i<32; i++) {                         /* basic cycle start */
        sum += delta;
        v0 += ((v1<<4) + k0) ^ (v1 + sum) ^ ((v1>>5) + k1);
        v1 += ((v0<<4) + k2) ^ (v0 + sum) ^ ((v0>>5) + k3);
    }                                              /* end cycle */
    v[0]=v0; v[1]=v1;
}

void decrypt (uint32_t v[2], uint32_t k[4]) {
    uint32_t v0=v[0], v1=v[1], sum=0xC6EF3720, i;  /* set up; sum is 32*delta */
    uint32_t delta=0x9E3779B9;                     /* a key schedule constant */
    uint32_t k0=k[0], k1=k[1], k2=k[2], k3=k[3];   /* cache key */
    for (i=0; i<32; i++) {                         /* basic cycle start */
        v1 -= ((v0<<4) + k2) ^ (v0 + sum) ^ ((v0>>5) + k3);
        v0 -= ((v1<<4) + k0) ^ (v1 + sum) ^ ((v1>>5) + k1);
        sum -= delta;
    }                                              /* end cycle */
    v[0]=v0; v[1]=v1;
}

Note that the reference implementation acts on multi-byte numeric values. The original paper does not specify how to derive the numbers it acts on from binary or other content.

See also

  • RC4 – A stream cipher that, just like TEA, is designed to be very simple to implement.
  • XTEA – First version of Block TEA's successor.
  • XXTEA – Corrected Block TEA's successor.
  • Treyfer – A simple and compact encryption algorithm with 64 bit key size and block size.

Notes

  1. ^ Matthew D. Russell (27 Feb 2004). "Tinyness: An Overview of TEA and Related Ciphers". Archived from the original on 12 August 2007.
  2. ^ a b Kelsey, John; Schneier, Bruce; Wagner, David (1997). Related-key cryptanalysis of 3-WAY, Biham-DES, CAST, DES-X NewDES, RC2, and TEA. Vol. 1334. pp. 233–246. CiteSeerX 10.1.1.35.8112. doi:10.1007/BFb0028479. ISBN 978-3-540-63696-0. {{cite book}}: |journal= ignored (help)
  3. ^ Bogdanov, Andrey; Wang, Meiqin (2012). Zero-Correlation Linear Cryptanalysis with Reduced Data Complexity (PDF). Vol. 7549. Fast Software Encryption 2012. pp. 29–48. doi:10.1007/978-3-642-34047-5_3. ISBN 978-3-642-34046-8. {{cite book}}: |journal= ignored (help)
  4. ^ a b c Wheeler, David J.; Needham, Roger M. (1994-12-16). TEA, a tiny encryption algorithm. Vol. 1008. Leuven, Belgium: Fast Software Encryption: Second International Workshop. pp. 363–366. doi:10.1007/3-540-60590-8_29. ISBN 978-3-540-60590-4. {{cite book}}: |journal= ignored (help)
  5. ^ Kelsey, John; Schneier, Bruce; Wagner, David (1996). Key-schedule cryptanalysis of IDEA, G-DES, GOST, SAFER, and Triple-DES (PDF). Vol. 1109. pp. 237–251. doi:10.1007/3-540-68697-5_19. ISBN 978-3-540-61512-5. {{cite book}}: |journal= ignored (help)
  6. ^ Michael Steil. "17 Mistakes Microsoft Made in the Xbox Security System". Archived from the original on 16 April 2009.

References

Retrieved from "https://en.wikipedia.org/w/index.php?title=Tiny_Encryption_Algorithm&oldid=899492571"