Jump to content

User:Tucania/sandbox

From Wikipedia, the free encyclopedia

Segmentation

[edit]
File:Segmented brain.jpg
A T1 MRI image of the brain (left), and the same image with a manual segmentation overlaid on top (right).

Segmentation is the process of partitioning an image into different segments. In medical imaging, these segments often correspond to different tissue classes, organs, pathologies, or other biologically relevant structures. Medical image segmentation is made difficult by low contrast, noise, and other imaging ambiguities. Although there are many computer vision techniques for image segmentation, some have been adapted specifically for medical image computing. Below is a sampling of techniques within this field; the implementation relies on the expertise that clinicians can provide.

  • Atlas-Based Segmentation: For many applications, a clinical expert can manually label several images; segmenting unseen images is a matter of extrapolating from these manually labeled training images. Methods of this style are typically referred to as atlas-based segmentation methods. Parametric atlas methods typically combine these training images into a single atlas image [1], while nonparametric atlas methods typically use all of the training images separately [2]. Atlas-based methods usually require the use of image registration in order to align the atlas image or images to a new, unseen image.
  • Shape-Based Segmentation: Many methods parametrize a template shape for a given structure, often relying on control points along the boundary. The entire shape is then deformed to match a new image. Two of the most common shape-based techniques are Active Shape Models [3] and Active Appearance Models [4]. These methods have been very influential, and have given rise to similar models.
  • Interactive Segmentation: Interactive methods are useful when clinicians can provide some information, such as a seed region or rough outline of the region to segment. An algorithm can then iteratively refine such a segmentation, with or without guidance from the clinician.


Registration

[edit]
CT image (left), PET image (center) and overlay of both (right) after correct registration.

Image registration is a process that searches for the correct alignment of images[5] [6] [7] [8]. In the simplest case, we would like to align two images. Typically, one image is treated as the target image and the other is treated as a source image; the source image is transformed to match the target image. The optimization procedure updates the transformation of the source image based on a similarity value that evaluates the current quality of the alignment. This iterative procedure is repeated until a (local) optimum is found. An example is the registration of CT and PET images to combine structural and metabolic information (see figure).

Image registration is used in a variety of medical applications:

  • Studying temporal changes. Longitudinal studies acquire images over several months or years to study long-term processes, such as disease progression. Time series correspond to images acquired within the same session (seconds or minutes). They can be used to study cognitive processes, heart deformations and respiration.
  • Combining complementary information from different imaging modalities. An example is the fusion of anatomical and functional information. Since the size and shape of structures vary across modalities, it is more challenging to evaluate the alignment quality. This has lead to the use of similarity measures such as mutual information[9].
  • Characterizing a population of subjects. In contrast to intra-subject registration, a one-to-one mapping may not exist between subjects, depending on the structural variability of the organ of interest. Inter-subject registration is required for atlas construction in computational anatomy [10]. Here, the objective is to statistically model the anatomy of organs across subjects.

There are several important considerations when performing image registration:

  • The transformation model. Common choices are rigid, affine, and deformable transformation models. B-spline and thin plate spline models are commonly used for parameterized transformation fields. Non-parametric or dense deformation fields carry a displacement vector at every grid location; this necessitates additional regularization constraints. A specific class of deformation fields are diffeomorphisms, which are invertible transformations with a smooth inverse.
  • The similarity metric. A distance or similarity function is used to quantify the registration quality. This similarity can be calculated either on the original images or on features extracted from the images. Common similarity measures are sum of squared distances (SSD), correlation coefficient, and mutual information. The choice of similarity measure depends on whether the images are from the same modality; the acquisition noise can also play a role in this decision. For example, SSD is the optimal similarity measure for images of the same modality with Gaussian noise[11]. However, the image statistics in ultrasound are significantly different to Gaussian noise, leading to the introduction of ultrasound specific similarity measures. Multi-modal registration requires a more sophisticated similarity measure; alternatively, a different image representation can be used, such as structural representations[12].
  • The optimization procedure. Either continuous or discrete optimization is performed. For continuous optimization, gradient-based optimization techniques are applied to improve the convergence speed.


Atlases

[edit]

Medical images can vary significantly across individuals due to people having organs of different shapes and sizes. Therefore, representing medical images to account for this variability is crucial. A popular approach to represent medical images is through the use of one or more atlases. Here, an atlas refers to a specific model for a population of images with parameters that are learned from a training dataset [13][14].

The simplest example of an atlas is a mean intensity image, commonly referred to as a template. However, an atlas can also include richer information, such as local image statistics and the probability that a particular spatial location has a certain label. New medical images, which are not used during training, can be mapped to an atlas, which has been tailored to the specific application, such as segmentation and group analysis. Mapping an image to an atlas usually involves registering the image and the atlas. This deformation can be used to address variability in medical images.

Single template

[edit]

The simplest approach is to model medical images as deformed versions of a single template image. For example, anatomical MRI brain scans are often mapped to the MNI template [15] as to represent all the brain scans in common coordinates. The main drawback of a single-template approach is that if there are significant differences between the template and a given test image, then there may not be a good way to map one onto the other. For example, an anatomical MRI brain scan of a patient with severe brain abnormalities (i.e., a tumor or surgical procedure), may not easily map to the MNI template.

Multiple templates

[edit]

Rather than relying on a single template, multiple templates can be used. The idea is to represent an image as a deformed version of one of the templates. For example, there could be one template for a healthy population and one template for a diseased population. However, in many applications, it is not clear how many templates are needed. A simple albeit computationally expensive way to deal with this is to have every image in a training dataset be a template image and thus every new image encountered is compared against every image in the training dataset. A more recent approach automatically finds the number of templates needed [16].


Statistical Analysis

[edit]

Statistical methods combine the medical imaging field with modern Computer Vision, Machine Learning and Pattern Recognition. Over the last decade, several large datasets have been made publicly available (see for example ADNI, 1000 functional Connectomes Project), in part due to collaboration between various institutes and research centers. This increase in data size calls for new algorithms that can mine and detect subtle changes in the images to address clinical questions. Such clinical questions are very diverse and include group analysis, imaging biomarkers, disease phenotyping and longitudinal studies.

Group Analysis

[edit]

In the Group Analysis, the objective is to detect and quantize abnormalities induced by a disease by comparing the images of two or more cohorts. Usually one of these cohorts consist of normal (control) subjects, and the other one consists of abnormal patients. Variation caused by the disease can manifest itself as abnormal deformation of anatomy (see Voxel-based morphometry). For example, shrinkage of sub-cortical tissues such as the Hippocampus in brain may be linked to Alzheimer’s disease. Additionally, changes in biochemical (functional) activity can be observed using imaging modalities such as Positron Emission Tomography.

The comparison between groups is usually conducted on the voxel level. Hence, the most popular pre-processing pipeline, particularly in neuroimaging, transforms all of the images in a dataset to a common coordinate frame via (Medical Image Registration) in order to maintain correspondence between voxels. Given this voxel-wise correspondence, the most common Frequentist method is to extract a statistic for each voxel (for example, the mean voxel intensity for each group) and perform statistical hypothesis testing to evaluate whether a null hypothesis is or is not supported. The null hypothesis typically assumes that the two cohorts are drawn from the same distribution, and hence, should have the same statistical properties (for example, the mean values of two groups are equal for a particular voxel). Since medical images contain large numbers of voxels, the issue of multiple comparison needs to be addressed [17], [18]. There are also Bayesian approach to tackle group analysis problem [19].

Classification

[edit]

Although group analysis can quantify the general effects of a pathology on an anatomy and function, it does not provide subject level measures, and hence cannot be used as biomarkers for diagnosis (see Imaging Biomarkers). Clinicians, on the other hand, are often interested in early diagnosis of the pathology (i.e. classification [20], [21]) and in learning the progression of a disease (i.e. regression [22]). From methodological point of view, current techniques varies from applying standard machine learning algorithms to medical imaging datasets (e.g. Support Vector Machine [23]), to developing new approaches adapted for the needs of the field[24]. The main difficulties are as follows:

  • Small sample size (Curse of Dimensionality): a large medical imaging dataset contains hundreds to thousands of images, whereas the number of voxels in a typical volumetric image can easily go beyond millions. A remedy to this problem is to reduce the number of features in an informative sense (see dimensionality reduction). Several unsupervised and semi-/supervised[24],[25],[26],[27] approaches have been proposed to address this issue.
  • Interpretability: A good generalization accuracy is not always the primary objective, as clinicians would like to understand which parts of anatomy are affected by the disease. Therefore, interpretability of the results is very important; methods that ignore the image structure are not favored. Alternative methods based on feature selection have been proposed[25], [26],[27].

Clustering

[edit]

Image-based pattern classification methods typically assume that the neurological effects of a disease are distinct and well defined. This may not always be the case. For a number of medical conditions, the patient populations are highly heterogeneous, and further categorization into sub-conditions has not been established. Additionally, some diseases (e.g., Autism Spectrum Disorder (ASD), Schizophrenia, Mild cognitive impairment (MCI)) can be characterized by a continuous or nearly-continuous spectra from mild cognitive impairment to very pronounced pathological changes. To facilitate image-based analysis of heterogeneous disorders, methodological alternatives to pattern classification have been developed. These techniques borrow ideas from high-dimensional clustering [28] and high-dimensional pattern-regression to cluster a given population into homogeneous sub-populations. The goal is to provide a better quantitative understanding of the disease within each sub-population.

Biomechanical Modeling

[edit]

Modality Specific Computing

[edit]

Diffusion MRI

[edit]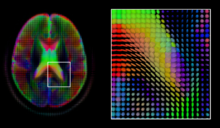
A mid-axial slice of the ICBM diffusion tensor image template. Each voxel's value is a tensor represented here by an ellipsoid. Color denotes principal orientation: red = left-right, blue=inferior-superior, green = posterior-anterior

Diffusion MRI is a structural magnetic resonance imaging modality that allows measurement of the diffusion process of molecules. Diffusion is measured by applying a gradient pulse to a magnetic field along a particular direction. In a typical acquisition, a set of uniformally distributed gradient directions is used to create a set of diffusion weighted volumes. In addition, an unweighted volume is acquired under the same magnetic field without application of a gradient pulse. As each acquisition is associated with multiple volumes, diffusion MRI has created a variety of unique challenges in medical image computing.

In medicine, there are two major computational goals in diffusion MRI:

  • Estimation of local tissue properties, such as diffusivity;
  • Estimation of local directions and global pathways of diffusion.

The diffusion tensor [29], a 3 × 3 symmetric positive-definite matrix, offers a straightforward solution to both of these goals. It is proportional to the covariance matrix of a Normally distributed local diffusion profile and, thus, the dominant eigenvector of this matrix is the principal direction of local diffusion. Due to the simplicity of this model, a maximum likelihood estimate of the diffusion tensor can be found by simply solving a system of linear equations at each location independently. However, as the volume is assumed to contain contiguous tissue fibers, it may be preferable to estimate the volume of diffusion tensors in its entirety by imposing regualarity conditions on the underlying field of tensors [30]. Scalar values can be extracted from the diffusion tensor, such as the fractional anisotropy, mean, axial and radial diffusivities, which indirectly measure tissue properties such as the dysmyelination of axonal fibers [31] or the presence of edema [32]. Standard scalar image computing methods, such as registration and segmentation, can be applied directly to volumes of such scalar values. However, to fully exploit the information in the diffusion tensor, these methods have been adapted to account for tensor valued volumes when performing registration [33] [34] and segmentation [35].

Given the principal direction of diffusion at each location in the volume, it is possible to estimate the global pathways of diffusion through a process known as tractography [36]. However, due to the relatively low resolution of diffusion MRI, many of these pathways may cross, kiss or fan at a single location. In this situation, the single principal direction of the diffusion tensor is not an appropriate model for the local diffusion distribution. The most common solution to this problem is to estimate multiple directions of local diffusion using more complex models. These include mixtures of diffusion tensors [37], Q-ball imaging [38], diffusion spectrum imaging [39] and fiber orientation distribution functions [40] [41], which typically require HARDI acquisition with a large number of gradient directions. As with the diffusion tensor, volumes valued with these complex models require special treatment when applying image computing methods, such as registration [42] and segmentation [43].

Functional MRI

[edit]

Functional magnetic resonance imaging (fMRI) is a medical imaging modality that indirectly measures neural activity by observing the local hemodynamics, or blood oxygen level dependent signal (BOLD). fMRI data offers a range of insights, and can be roughly divided into two categories:

  • Task related fMRI is acquired as the subject is performing a sequence of timed experimental conditions. In block-design experiments, the conditions are present for short periods of time (e.g., 10 seconds) and are alternated with periods of rest. Event-related experiments rely on a random sequence of stimuli and use a single time point to denote each condition. The standard approach to analyze task related fMRI is the general linear model (GLM) [44]
  • Resting state fMRI is acquired in the absence of any experimental task. Typically, the objective is to study the intrinsic network structure of the brain. Observations made during rest have also been linked to specific cognitive processes such as encoding or reflection. Most studies of resting state fMRI focus on low frequency fluctuations of the fMRI signal (LF-BOLD). Seminal discoveries include the default network [45], a comprehensive cortical parcellation [46], and the linking of network characteristics to behavioral parameters.

There is a rich set of methodology used to analyze functional neuroimaging data, and there is often no consensus regarding the best method. Instead, researchers approach each problem independently and select a suitable model/algorithm. In this context there is a relatively active exchange among neuroscience, computational biology, statistics, and machine learning communities. Prominent approaches include

  • Massive univariate approaches that probe individual voxels in the imaging data for a relationship to the experiment condition. The prime approach is the general linear model (GLM) [44]
  • Multivariate- and classifier based approaches, often referred to as multi voxel pattern analysis or multi-variate pattern analysis probe the data for global and potentially distributed responses to an experimental condition. Early approaches used support vector machines (SVM) to study responses to visual stimuli [47]. Recently, alternative pattern recognition algorithms have been explored, such as random forest based gini contrast [48] or sparse regression and dictionary learning [49]
  • Functional connectivity analysis studies the intrinsic network structure of the brain, including the interactions between regions. The majority of such studies focus on resting state data to parcelate the brain [46] or to find correlates to behavioral measures [50]. Task specific data can be used to study causal relationships among brain regions (e.g., dynamic causal mapping (DCM) [51]).

When working with large cohorts of subjects, the normalization (registration) of individual subjects into a common reference frame is crucial. A body of work and tools exist to perform normalization based on anatomy (FSL, FreeSurfer, SPM). Alignment taking spatial variability across subjects into account is a more recent line of work. Examples are the alignment of the cortex based on fMRI signal correlation [52], the alignment based on the global functional connectivity structure both in task-, or resting state data [53], and the alignemnt based on stimulus specific activation profiles of individual voxels [54].

Software

[edit]

Software for medical image analysis ranges from general packages, which implement standard algorithms, to specialized tools, which focus on a specific organ.

All-Purpose Packages

[edit]

Brain Imaging

[edit]


References

[edit]
  1. ^ J Gee, M Reivich, R Bajcsy (1993). "Elastically Deforming a Three-Dimensional Atlas to Match Anatomical Brain Images". Journal of Computer Assisted Tomography. 17 (1): 225–236.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  2. ^ MR Sabuncu, BT Yeo, K Van Leemput, B Fischl, P Golland (June 2010). "A Generative Model for Image Segmentation Based on Label Fusion". IEEE Transactions on Medical Imaging. 29 (10): 1714–1729. doi:10.1109/TMI.2010.2050897.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  3. ^ Cootes TF, Taylor CJ, Cooper DH, and Graham J (1995). "Active shape models-their training and application". Computer vision and image understanding. 61 (1). San Diego: Academic Press, c1995-: 38–59.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  4. ^ Cootes, T.F. and Edwards, G.J. and Taylor, C.J. (2001). "Active appearance models". Pattern Analysis and Machine Intelligence, IEEE Transactions on. 23 (6). IEEE: 681–685.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  5. ^ Lisa Gottesfeld Brown (1992). "A survey of image registration techniques". ACM Computing Surveys (CSUR). {{cite journal}}: Unknown parameter |Issue= ignored (|issue= suggested) (help); Unknown parameter |Pages= ignored (|pages= suggested) (help); Unknown parameter |Volume= ignored (|volume= suggested) (help)
  6. ^ J. Maintz and M. Viergever (1998). "A survey of medical image registration". Medical Image Analysis: 1–36.
  7. ^ J. Hajnal, D. Hawkes, and D. Hill (2001). Medical Image Registration. Baton Rouge, Florida: CRC Press.{{cite book}}: CS1 maint: multiple names: authors list (link)
  8. ^ Barbara Zitová, Jan Flusser (2003). "Image registration methods: a survey". Image Vision Comput.: 977–1000. {{cite journal}}: Unknown parameter |Issue= ignored (|issue= suggested) (help); Unknown parameter |Volume= ignored (|volume= suggested) (help)
  9. ^ J. P. W. Pluim, J. B. A. Maintz, and M. A. Viergever. "Mutual information based registration of medical images: A survey". IEEE Trans. Med. Imaging. {{cite journal}}: Unknown parameter |22(8):986–1004, year= ignored (help)CS1 maint: multiple names: authors list (link)
  10. ^ Grenander, Ulf and Miller, Michael I. (1998). "Computational anatomy: an emerging discipline". Q. Appl. Math. {{cite journal}}: Unknown parameter |Number= ignored (|number= suggested) (help); Unknown parameter |Pages= ignored (|pages= suggested) (help); Unknown parameter |Volume= ignored (|volume= suggested) (help)CS1 maint: multiple names: authors list (link)
  11. ^ P. A. Viola (1995). Alignment by Maximization of Mutual Information (Thesis). {{cite thesis}}: Unknown parameter |institute= ignored (help)
  12. ^ C. Wachinger, N. Navab (2012). "Entropy and Laplacian images: structural representations for multi-modal registration". Medical Image Analysis. {{cite journal}}: Unknown parameter |Issue= ignored (|issue= suggested) (help); Unknown parameter |Pages= ignored (|pages= suggested) (help); Unknown parameter |Volume= ignored (|volume= suggested) (help)
  13. ^ M. De Craene and A. B. d Aische and B. Macq and S. K. Warfield. "Multi-subject registration for unbiased statistical atlas construction". Proceedings of Medical Image Computing and Computer-Assisted Intervention 2004.
  14. ^ C. J. Twining and T. Cootes and S. Marsland and V. Petrovic and R. Schestowitz and C. Taylor. "A unified information-theoretic approach to groupwise non-rigid registration and model building". Proceedings of Information Processing in Medical Imaging 2005.
  15. ^ "The MNI brain and the Talairach atlas".
  16. ^ M. Sabuncu and S. K. Balci and M. E. Shenton and P. Golland (2009). "Image-driven Population Analysis through Mixture Modeling". IEEE Transactions in Medical Imaging. 28 (9): 1473–1487.
  17. ^ J. Ashburner and K.J. Friston (2000). "Voxel-Based Morphometry -- The Methods". NeuroImage: 805–821.
  18. ^ C. Davatzikos (2004.). "Why voxel-based morphometric analysis should be used with great caution when characterizing group differences,". NeuroImage: 17–20. {{cite journal}}: Check date values in: |year= (help)CS1 maint: year (link)
  19. ^ K.J. Friston, W.D. Penny, C. Phillips, S.J. Kiebel, G. Hinton, and J. Ashburner (2002.). "Classical and Bayesian Inference in Neuroimaging: Theory". NeuroImage: 465–483. {{cite journal}}: Check date values in: |year= (help)CS1 maint: multiple names: authors list (link) CS1 maint: year (link)
  20. ^ Yong Fan, Nematollah Batmanghelich, Chris M. Clark, Christos Davatzikos, the Alzheimer’s Disease Neuroimaging Initiative, Spatial patterns of brain atrophy in MCI patients, identified via high-dimensional pattern classification, predict subsequent cognitive decline. (2008.). NeuroImage (4): 1731–1743. {{cite journal}}: Check date values in: |year= (help); Missing or empty |title= (help); Unknown parameter |Volume= ignored (|volume= suggested) (help)CS1 maint: multiple names: authors list (link) CS1 maint: year (link)
  21. ^ Rémi Cuingnet and Emilie Gerardin and Jérôme Tessieras and Guillaume Auzias and Stéphane Lehéricy and Marie-Odile Habert and Marie Chupin and Habib Benali and Olivier Colliot (2011). "The Alzheimer's Disease Neuroimaging Initiative, Automatic classification of patients with Alzheimer's disease from structural MRI: A comparison of ten methods using the ADNI database" (2): 766–781. {{cite journal}}: Cite journal requires |journal= (help); Unknown parameter |Volume= ignored (|volume= suggested) (help)
  22. ^ Y. Wang and Y. Fan and P. Bhatt P and C. Davatzikos (2010). "High-dimensional pattern regression using machine learning: from medical images to continuous clinical variables". Neuroimage. 50 (4): 1519–35.
  23. ^ Benoît Magnin and Lilia Mesrob and Serge Kinkingnéhun and Mélanie Pélégrini-Issac and Olivier Colliot and Marie Sarazin and Bruno Dubois and Stéphane Lehéricy and Habib Benali (2009). "Support vector machine-based classification of Alzheimer's disease from whole-brain anatomical MRI". Neuroradiology. 51 (2): 73–83.
  24. ^ a b N.K. Batmanghelich and B. Taskar and C. Davatzikos (2012). "Generative-discriminative basis learning for medical imaging". IEEE Trans Med Imaging. 31 (1): 51–69.
  25. ^ a b Glenn Fung and Jonathan Stoeckel (2007). "SVM feature selection for classification of SPECT images of Alzheimer's disease using spatial information". Knowledge and Information Systems. 11 (2): 243–258.
  26. ^ a b R. Chaves and J. Ramírez and J.M. Górriz and M. López and D. Salas-Gonzalez and I. Álvarez and F. Segovia (2009). "SVM-based computer-aided diagnosis of the Alzheimer's disease using t-test NMSE feature selection with feature correlation weighting". Neuroscience Letters. 461 (3): 293–297.
  27. ^ a b yanxi liu and leonid teverovskiy and owen carmichael and ron kikinis and martha shenton and cameron s. carter and v. andrew stenger and simon davis and howard aizenstein and james t. becker (2004). "discriminative mr image feature analysis for automatic schizophrenia and alzheimer's disease classification". medical image computing and computer-assisted intervention – miccai.
  28. ^ R. Filipovych and S. M. Resnick and C. Davatzikos (2011). "Semi-supervised cluster analysis of imaging data". Neuroimage. 54 (3): 2185–2197.
  29. ^ P Basser, J Mattiello, D LeBihan (January 1994). "MR diffusion tensor spectroscopy, imaging". Biophysical Journal. 66 (1): 259–267. doi:10.1.1.162.2887. {{cite journal}}: Check |doi= value (help)CS1 maint: multiple names: authors list (link)
  30. ^ P Fillard, X Pennec, V Arsigny, N Ayache (November 2007). "Clinical DT-MRI estimation, smoothing,, fiber tracking with log-Euclidean metrics". IEEE Transactions on Medical Imaging. 26 (11): 1472–1482. doi:10.1109/TMI.2007.899173.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  31. ^ S-K Song, S-W Sun, M Ramsbottom, C Cheng, J Russell, A Cross (November 2002). "Dysmyelination Revealed through MRI as Increased Radial (but Unchanged Axial) Diffusion of Water". NeuroImage. 13 (3): 1429–1436. doi:10.1006/nimg.2002.1267.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  32. ^ P Barzo, A Marmarou, P Fatouros, K Hayasaki, F Corwin (December 1997). "Contribution of vasogenic and cellular edema to traumatic brain swelling measured by diffusion-weighted imaging". Journal of Neurosurgery. 87 (6): 900–907. doi:10.3171/jns.1997.87.6.0900.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  33. ^ D Alexander, C Pierpaoli, P Basser (January 2001). "Spatial transformation of diffusion tensor magnetic resonance images". IEEE Transactions on Medical Imaging. 20 (11): 1131–1139. doi:10.1.1.162.2954. {{cite journal}}: Check |doi= value (help)CS1 maint: multiple names: authors list (link)
  34. ^ Y Cao, M Miller, S Mori, R Winslow, L Younes (June 2006). "Diffeomorphic Matching of Diffusion Tensor Images". Proceedings of IEEE Computer Society Conference on Computer Vision, Pattern Recognition (CVPR), Workshop on Mathematical Methods in Biomedical Image Analysis (MMBIA 2006). New York. doi:10.1109/CVPRW.2006.65. {{cite conference}}: Text "pages 67-67" ignored (help)CS1 maint: multiple names: authors list (link)
  35. ^ Z Wang, B Vemuri (October 2005). "DTI segmentation using an information theoretic tensor dissimilarity measure". IEEE Transactions on Medical Imaging. 24 (10): 1267–1277. doi:10.1109/TMI.2005.854516. {{cite journal}}: Text "ref Wang2005" ignored (help)
  36. ^ S Mori, B Crain, V Chacko, P van Zijl (February 1999). "Three-dimensional tracking of axonal projections in the brain by magnetic resonance imaging". Annals of Neurology. 45 (2): 265–269. doi:10.1002/1531-8249(199902)45:2<265::AID-ANA21>3.0.CO;2-3.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  37. ^ D Tuch, T Reese, M Wiegell, N Makris, J Belliveau, V Wedeen (October 2002). "High angular resolution diffusion imaging reveals intravoxel white matter fiber heterogeneity". Magnetic Resonance in Medicine. 48 (4): 577–582. doi:10.1.1.162.2345. {{cite journal}}: Check |doi= value (help)CS1 maint: multiple names: authors list (link)
  38. ^ D Tuch (December 2004). "Q-ball imaging". Magnetic Resonance in Medicine. 52 (6): 1358–1372. doi:10.1002/mrm.20279.
  39. ^ V Wedeen, P Hagmann, W-Y Tseng, T Reese (December 2005). "Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging". Magnetic Resonance in Medicine. 64 (6): 1377–1386. doi:10.1002/mrm.20642.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  40. ^ K Jansons, D Alexander (July 2003). "Persistent angular structure: new insights from diffusion magnetic resonance imaging data". Proceedings of Information Processing in Medical Imaging (IPMI) 2003, LNCS 2732. pp. 672–683. doi:10.1007/978-3-540-45087-0_56. {{cite conference}}: Unknown parameter |booktitle= ignored (|book-title= suggested) (help)
  41. ^ J-D Tournier, F Calamante, D Gadian, A Connelly (2007). "Direct estimation of the fiber orientation density function from diffusion-weighted MRI data using spherical deconvolution". NeuroImage. 23: 1176–1185. doi:10.1016/j.neuroimage.2004.07.037.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  42. ^ X Geng, T Ross, W Zhan, H Gu, Y-P Chao, C-P Lin, G Christensen, N Schuff, Y Yang (July 2009). "Diffusion MRI Registration Using Orientation Distribution Functions". Proceedings of Information Processing in Medical Imaging (IPMI) 2009, LNCS 5636. Vol. 21. pp. 626–637. doi:10.1007/978-3-642-02498-6_52. {{cite conference}}: Unknown parameter |booktitle= ignored (|book-title= suggested) (help)CS1 maint: multiple names: authors list (link)
  43. ^ M Descoteaux, R Deriche (September 2007). "Segmentation of Q-Ball Images Using Statistical Surface Evolution". Proceedings of Medical Image Computing and Computer-Assisted Intervention (MICCAI) 2007 , LNCS 4792. pp. 769–776. doi:10.1007/978-3-540-75759-7_93. {{cite conference}}: Unknown parameter |booktitle= ignored (|book-title= suggested) (help)
  44. ^ a b Friston, K., Holmes, A., Worsley, K., Poline, J., Frith, C., Frackowiak, R.; et al. (1995). "Statistical parametric maps in functional imaging: a general linear approach". Hum Brain Mapp: 189--210. {{cite journal}}: Explicit use of et al. in: |author= (help); Unknown parameter |Issue= ignored (|issue= suggested) (help); Unknown parameter |Volume= ignored (|volume= suggested) (help)CS1 maint: multiple names: authors list (link)
  45. ^ Buckner, R. L., Andrews-Hanna, J. R., and Schacter, D. L. (2008). "The brain's default network: anatomy, function, and relevance to disease". Ann N Y Acad Sci: 1–38. {{cite journal}}: Cite has empty unknown parameter: |Issue= (help); Unknown parameter |Volume= ignored (|volume= suggested) (help)CS1 maint: multiple names: authors list (link)
  46. ^ a b Yeo, B. T. T., Krienen, F. M., Sepulcre, J., Sabuncu, M. R., Lashkari, D., Hollinshead, M., Roffman, J. L., Smoller, J. W., Zöllei, L., Polimeni, J. R., Fischl, B., Liu, H., and Buckner, R. L. (2011). "The organization of the human cerebral cortex estimated by intrinsic functional connectivity". J Neurophysiol: 1125–65. {{cite journal}}: Unknown parameter |Issue= ignored (|issue= suggested) (help); Unknown parameter |Volume= ignored (|volume= suggested) (help)CS1 maint: multiple names: authors list (link)
  47. ^ J. V. Haxby, M. I. Gobbini, M. L. Furey, A. Ishai, J. L. Schouten, and P. Pietrini (2001). "Distributed and overlapping representations of faces and objects in ventral temporal cortex". Science.: 2425–30. {{cite journal}}: Unknown parameter |Issue= ignored (|issue= suggested) (help); Unknown parameter |Volume= ignored (|volume= suggested) (help)CS1 maint: multiple names: authors list (link)
  48. ^ Langs, G., Menze, B. H., Lashkari, D., and Golland, P. (2011). "Detecting stable distributed patterns of brain activation using Gini contrast". NeuroImage: 497–507. {{cite journal}}: Unknown parameter |Issue= ignored (|issue= suggested) (help); Unknown parameter |Volume= ignored (|volume= suggested) (help)CS1 maint: multiple names: authors list (link)
  49. ^ Varoquaux, G., Gramfort, A., Pedregosa, F., Michel, V., and Thirion, B. (2011). "Multi-subject dictionary learning to segment an atlas of brain spontaneous activity". Inf Process Med Imaging. pp. 562–73. {{cite conference}}: Cite has empty unknown parameter: |Issue= (help); Unknown parameter |Volume= ignored (|volume= suggested) (help)CS1 maint: multiple names: authors list (link)
  50. ^ van den Heuvel, M. P., Stam, C. J., Kahn, R. S., and Hulshoff Pol, H. E. (2009). "Efficiency of functional brain networks and intellectual performance". J Neurosci: 7619–24. {{cite journal}}: Unknown parameter |Issue= ignored (|issue= suggested) (help); Unknown parameter |Volume= ignored (|volume= suggested) (help)CS1 maint: multiple names: authors list (link)
  51. ^ Friston, K. (2003). "Dynamic causal modelling". Neuroimage: 1273--1302. {{cite journal}}: Unknown parameter |Issue= ignored (|issue= suggested) (help); Unknown parameter |Volume= ignored (|volume= suggested) (help)
  52. ^ Sabuncu, M. R., Singer, B. D., Conroy, B., Bryan, R. E., Ramadge, P. J., and Haxby, J. V. (2010). "Function-based Intersubject Alignment of Human Cortical Anatomy". Cerebral Cortex: 130–140. {{cite journal}}: Unknown parameter |Issue= ignored (|issue= suggested) (help); Unknown parameter |Volume= ignored (|volume= suggested) (help)CS1 maint: multiple names: authors list (link)
  53. ^ Langs, G., Lashkari, D., Sweet, A., Tie, Y., Rigolo, L., Golby, A. J., and Golland, P. (2011). "Learning an atlas of a cognitive process in its functional geometry". Inf Process Med Imaging. pp. 135–46. {{cite conference}}: Unknown parameter |Volume= ignored (|volume= suggested) (help)CS1 maint: multiple names: authors list (link)
  54. ^ Haxby, J. V., Guntupalli, J. S., Connolly, A. C., Halchenko, Y. O., Conroy, B. R., Gobbini, M. I., Hanke, M., and Ramadge, P. J. (2011). "A common, high-dimensional model of the representational space in human ventral temporal cortex". Neuron: 404--416. {{cite journal}}: Unknown parameter |Issue= ignored (|issue= suggested) (help); Unknown parameter |Volume= ignored (|volume= suggested) (help)CS1 maint: multiple names: authors list (link)
Retrieved from "https://en.wikipedia.org/w/index.php?title=User:Tucania/sandbox&oldid=508805957"