Basis (linear algebra)

In mathematics, a set B of vectors in a vector space V is called a basis (pl.: bases) if every element of V may be written in a unique way as a finite linear combination of elements of B. The coefficients of this linear combination are referred to as components or coordinates of the vector with respect to B. The elements of a basis are called basis vectors.
Equivalently, a set B is a basis if its elements are linearly independent and every element of V is a linear combination of elements of B.[1] In other words, a basis is a linearly independent spanning set.
A vector space can have several bases; however all the bases have the same number of elements, called the dimension of the vector space.
This article deals mainly with finite-dimensional vector spaces. However, many of the principles are also valid for infinite-dimensional vector spaces.
Basis vectors find applications in the study of crystal structures and frames of reference.
Definition
[edit]A basis B of a vector space V over a field F (such as the real numbers R or the complex numbers C) is a linearly independent subset of V that spans V. This means that a subset B of V is a basis if it satisfies the two following conditions:
- linear independence
- for every finite subset of B, if for some in F, then ;
- spanning property
- for every vector v in V, one can choose in F and in B such that .
The scalars are called the coordinates of the vector v with respect to the basis B, and by the first property they are uniquely determined.
A vector space that has a finite basis is called finite-dimensional. In this case, the finite subset can be taken as B itself to check for linear independence in the above definition.
It is often convenient or even necessary to have an ordering on the basis vectors, for example, when discussing orientation, or when one considers the scalar coefficients of a vector with respect to a basis without referring explicitly to the basis elements. In this case, the ordering is necessary for associating each coefficient to the corresponding basis element. This ordering can be done by numbering the basis elements. In order to emphasize that an order has been chosen, one speaks of an ordered basis, which is therefore not simply an unstructured set, but a sequence, an indexed family, or similar; see § Ordered bases and coordinates below.
Examples
[edit]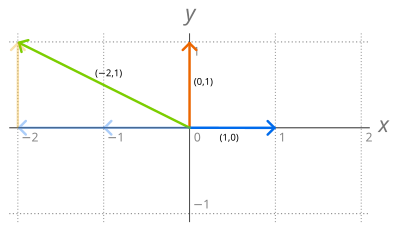
The set R2 of the ordered pairs of real numbers is a vector space under the operations of component-wise addition and scalar multiplication where is any real number. A simple basis of this vector space consists of the two vectors e1 = (1, 0) and e2 = (0, 1). These vectors form a basis (called the standard basis) because any vector v = (a, b) of R2 may be uniquely written as Any other pair of linearly independent vectors of R2, such as (1, 1) and (−1, 2), forms also a basis of R2.
More generally, if F is a field, the set of n-tuples of elements of F is a vector space for similarly defined addition and scalar multiplication. Let be the n-tuple with all components equal to 0, except the ith, which is 1. Then is a basis of which is called the standard basis of
A different flavor of example is given by polynomial rings. If F is a field, the collection F[X] of all polynomials in one indeterminate X with coefficients in F is an F-vector space. One basis for this space is the monomial basis B, consisting of all monomials: Any set of polynomials such that there is exactly one polynomial of each degree (such as the Bernstein basis polynomials or Chebyshev polynomials) is also a basis. (Such a set of polynomials is called a polynomial sequence.) But there are also many bases for F[X] that are not of this form.
Properties
[edit]Many properties of finite bases result from the Steinitz exchange lemma, which states that, for any vector space V, given a finite spanning set S and a linearly independent set L of n elements of V, one may replace n well-chosen elements of S by the elements of L to get a spanning set containing L, having its other elements in S, and having the same number of elements as S.
Most properties resulting from the Steinitz exchange lemma remain true when there is no finite spanning set, but their proofs in the infinite case generally require the axiom of choice or a weaker form of it, such as the ultrafilter lemma.
If V is a vector space over a field F, then:
- If L is a linearly independent subset of a spanning set S ⊆ V, then there is a basis B such that
- V has a basis (this is the preceding property with L being the empty set, and S = V).
- All bases of V have the same cardinality, which is called the dimension of V. This is the dimension theorem.
- A generating set S is a basis of V if and only if it is minimal, that is, no proper subset of S is also a generating set of V.
- A linearly independent set L is a basis if and only if it is maximal, that is, it is not a proper subset of any linearly independent set.
If V is a vector space of dimension n, then:
- A subset of V with n elements is a basis if and only if it is linearly independent.
- A subset of V with n elements is a basis if and only if it is a spanning set of V.
Coordinates
[edit]Let V be a vector space of finite dimension n over a field F, and be a basis of V. By definition of a basis, every v in V may be written, in a unique way, as where the coefficients are scalars (that is, elements of F), which are called the coordinates of v over B. However, if one talks of the set of the coefficients, one loses the correspondence between coefficients and basis elements, and several vectors may have the same set of coefficients. For example, and have the same set of coefficients {2, 3}, and are different. It is therefore often convenient to work with an ordered basis; this is typically done by indexing the basis elements by the first natural numbers. Then, the coordinates of a vector form a sequence similarly indexed, and a vector is completely characterized by the sequence of coordinates. An ordered basis, especially when used in conjunction with an origin, is also called a coordinate frame or simply a frame (for example, a Cartesian frame or an affine frame).
Let, as usual, be the set of the n-tuples of elements of F. This set is an F-vector space, with addition and scalar multiplication defined component-wise. The map is a linear isomorphism from the vector space onto V. In other words, is the coordinate space of V, and the n-tuple is the coordinate vector of v.
The inverse image by of is the n-tuple all of whose components are 0, except the ith that is 1. The form an ordered basis of , which is called its standard basis or canonical basis. The ordered basis B is the image by of the canonical basis of .
It follows from what precedes that every ordered basis is the image by a linear isomorphism of the canonical basis of , and that every linear isomorphism from onto V may be defined as the isomorphism that maps the canonical basis of onto a given ordered basis of V. In other words, it is equivalent to define an ordered basis of V, or a linear isomorphism from onto V.
Change of basis
[edit]Let V be a vector space of dimension n over a field F. Given two (ordered) bases and of V, it is often useful to express the coordinates of a vector x with respect to in terms of the coordinates with respect to This can be done by the change-of-basis formula, that is described below. The subscripts "old" and "new" have been chosen because it is customary to refer to and as the old basis and the new basis, respectively. It is useful to describe the old coordinates in terms of the new ones, because, in general, one has expressions involving the old coordinates, and if one wants to obtain equivalent expressions in terms of the new coordinates; this is obtained by replacing the old coordinates by their expressions in terms of the new coordinates.
Typically, the new basis vectors are given by their coordinates over the old basis, that is, If and are the coordinates of a vector x over the old and the new basis respectively, the change-of-basis formula is for i = 1, ..., n.
This formula may be concisely written in matrix notation. Let A be the matrix of the , and be the column vectors of the coordinates of v in the old and the new basis respectively, then the formula for changing coordinates is
The formula can be proven by considering the decomposition of the vector x on the two bases: one has and
The change-of-basis formula results then from the uniqueness of the decomposition of a vector over a basis, here ; that is for i = 1, ..., n.
Related notions
[edit]Free module
[edit]If one replaces the field occurring in the definition of a vector space by a ring, one gets the definition of a module. For modules, linear independence and spanning sets are defined exactly as for vector spaces, although "generating set" is more commonly used than that of "spanning set".
Like for vector spaces, a basis of a module is a linearly independent subset that is also a generating set. A major difference with the theory of vector spaces is that not every module has a basis. A module that has a basis is called a free module. Free modules play a fundamental role in module theory, as they may be used for describing the structure of non-free modules through free resolutions.
A module over the integers is exactly the same thing as an abelian group. Thus a free module over the integers is also a free abelian group. Free abelian groups have specific properties that are not shared by modules over other rings. Specifically, every subgroup of a free abelian group is a free abelian group, and, if G is a subgroup of a finitely generated free abelian group H (that is an abelian group that has a finite basis), then there is a basis of H and an integer 0 ≤ k ≤ n such that is a basis of G, for some nonzero integers . For details, see Free abelian group § Subgroups.
Analysis
[edit]In the context of infinite-dimensional vector spaces over the real or complex numbers, the term Hamel basis (named after Georg Hamel[2]) or algebraic basis can be used to refer to a basis as defined in this article. This is to make a distinction with other notions of "basis" that exist when infinite-dimensional vector spaces are endowed with extra structure. The most important alternatives are orthogonal bases on Hilbert spaces, Schauder bases, and Markushevich bases on normed linear spaces. In the case of the real numbers R viewed as a vector space over the field Q of rational numbers, Hamel bases are uncountable, and have specifically the cardinality of the continuum, which is the cardinal number , where (aleph-nought) is the smallest infinite cardinal, the cardinal of the integers.
The common feature of the other notions is that they permit the taking of infinite linear combinations of the basis vectors in order to generate the space. This, of course, requires that infinite sums are meaningfully defined on these spaces, as is the case for topological vector spaces – a large class of vector spaces including e.g. Hilbert spaces, Banach spaces, or Fréchet spaces.
The preference of other types of bases for infinite-dimensional spaces is justified by the fact that the Hamel basis becomes "too big" in Banach spaces: If X is an infinite-dimensional normed vector space that is complete (i.e. X is a Banach space), then any Hamel basis of X is necessarily uncountable. This is a consequence of the Baire category theorem. The completeness as well as infinite dimension are crucial assumptions in the previous claim. Indeed, finite-dimensional spaces have by definition finite bases and there are infinite-dimensional (non-complete) normed spaces that have countable Hamel bases. Consider , the space of the sequences of real numbers that have only finitely many non-zero elements, with the norm . Its standard basis, consisting of the sequences having only one non-zero element, which is equal to 1, is a countable Hamel basis.
Example
[edit]In the study of Fourier series, one learns that the functions {1} ∪ { sin(nx), cos(nx) : n = 1, 2, 3, ... } are an "orthogonal basis" of the (real or complex) vector space of all (real or complex valued) functions on the interval [0, 2π] that are square-integrable on this interval, i.e., functions f satisfying
The functions {1} ∪ { sin(nx), cos(nx) : n = 1, 2, 3, ... } are linearly independent, and every function f that is square-integrable on [0, 2π] is an "infinite linear combination" of them, in the sense that
for suitable (real or complex) coefficients ak, bk. But many[3] square-integrable functions cannot be represented as finite linear combinations of these basis functions, which therefore do not comprise a Hamel basis. Every Hamel basis of this space is much bigger than this merely countably infinite set of functions. Hamel bases of spaces of this kind are typically not useful, whereas orthonormal bases of these spaces are essential in Fourier analysis.
Geometry
[edit]The geometric notions of an affine space, projective space, convex set, and cone have related notions of basis.[4] An affine basis for an n-dimensional affine space is points in general linear position. A projective basis is points in general position, in a projective space of dimension n. A convex basis of a polytope is the set of the vertices of its convex hull. A cone basis[5] consists of one point by edge of a polygonal cone. See also a Hilbert basis (linear programming).
Random basis
[edit]For a probability distribution in Rn with a probability density function, such as the equidistribution in an n-dimensional ball with respect to Lebesgue measure, it can be shown that n randomly and independently chosen vectors will form a basis with probability one, which is due to the fact that n linearly dependent vectors x1, ..., xn in Rn should satisfy the equation det[x1 ⋯ xn] = 0 (zero determinant of the matrix with columns xi), and the set of zeros of a non-trivial polynomial has zero measure. This observation has led to techniques for approximating random bases.[6][7]

It is difficult to check numerically the linear dependence or exact orthogonality. Therefore, the notion of ε-orthogonality is used. For spaces with inner product, x is ε-orthogonal to y if (that is, cosine of the angle between x and y is less than ε).
In high dimensions, two independent random vectors are with high probability almost orthogonal, and the number of independent random vectors, which all are with given high probability pairwise almost orthogonal, grows exponentially with dimension. More precisely, consider equidistribution in n-dimensional ball. Choose N independent random vectors from a ball (they are independent and identically distributed). Let θ be a small positive number. Then for
| (Eq. 1) |
N random vectors are all pairwise ε-orthogonal with probability 1 − θ.[7] This N growth exponentially with dimension n and for sufficiently big n. This property of random bases is a manifestation of the so-called measure concentration phenomenon.[8]
The figure (right) illustrates distribution of lengths N of pairwise almost orthogonal chains of vectors that are independently randomly sampled from the n-dimensional cube [−1, 1]n as a function of dimension, n. A point is first randomly selected in the cube. The second point is randomly chosen in the same cube. If the angle between the vectors was within π/2 ± 0.037π/2 then the vector was retained. At the next step a new vector is generated in the same hypercube, and its angles with the previously generated vectors are evaluated. If these angles are within π/2 ± 0.037π/2 then the vector is retained. The process is repeated until the chain of almost orthogonality breaks, and the number of such pairwise almost orthogonal vectors (length of the chain) is recorded. For each n, 20 pairwise almost orthogonal chains were constructed numerically for each dimension. Distribution of the length of these chains is presented.
Proof that every vector space has a basis
[edit]Let V be any vector space over some field F. Let X be the set of all linearly independent subsets of V.
The set X is nonempty since the empty set is an independent subset of V, and it is partially ordered by inclusion, which is denoted, as usual, by ⊆.
Let Y be a subset of X that is totally ordered by ⊆, and let LY be the union of all the elements of Y (which are themselves certain subsets of V).
Since (Y, ⊆) is totally ordered, every finite subset of LY is a subset of an element of Y, which is a linearly independent subset of V, and hence LY is linearly independent. Thus LY is an element of X. Therefore, LY is an upper bound for Y in (X, ⊆): it is an element of X, that contains every element of Y.
As X is nonempty, and every totally ordered subset of (X, ⊆) has an upper bound in X, Zorn's lemma asserts that X has a maximal element. In other words, there exists some element Lmax of X satisfying the condition that whenever Lmax ⊆ L for some element L of X, then L = Lmax.
It remains to prove that Lmax is a basis of V. Since Lmax belongs to X, we already know that Lmax is a linearly independent subset of V.
If there were some vector w of V that is not in the span of Lmax, then w would not be an element of Lmax either. Let Lw = Lmax ∪ {w}. This set is an element of X, that is, it is a linearly independent subset of V (because w is not in the span of Lmax, and Lmax is independent). As Lmax ⊆ Lw, and Lmax ≠ Lw (because Lw contains the vector w that is not contained in Lmax), this contradicts the maximality of Lmax. Thus this shows that Lmax spans V.
Hence Lmax is linearly independent and spans V. It is thus a basis of V, and this proves that every vector space has a basis.
This proof relies on Zorn's lemma, which is equivalent to the axiom of choice. Conversely, it has been proved that if every vector space has a basis, then the axiom of choice is true.[9] Thus the two assertions are equivalent.
See also
[edit]- Basis of a matroid
- Basis of a linear program
- Change of basis – Coordinate change in linear algebra
- Frame of a vector space – Similar to the basis of a vector space, but not necessarily linearly independent
- Spherical basis – Basis used to express spherical tensors
Notes
[edit]- ^ Halmos, Paul Richard (1987). Finite-Dimensional Vector Spaces (4th ed.). New York: Springer. p. 10. ISBN 978-0-387-90093-3.
- ^ Hamel 1905
- ^ Note that one cannot say "most" because the cardinalities of the two sets (functions that can and cannot be represented with a finite number of basis functions) are the same.
- ^ Rees, Elmer G. (2005). Notes on Geometry. Berlin: Springer. p. 7. ISBN 978-3-540-12053-7.
- ^ Kuczma, Marek (1970). "Some remarks about additive functions on cones". Aequationes Mathematicae. 4 (3): 303–306. doi:10.1007/BF01844160. S2CID 189836213.
- ^ Igelnik, B.; Pao, Y.-H. (1995). "Stochastic choice of basis functions in adaptive function approximation and the functional-link net". IEEE Trans. Neural Netw. 6 (6): 1320–1329. doi:10.1109/72.471375. PMID 18263425.
- ^ a b c Gorban, Alexander N.; Tyukin, Ivan Y.; Prokhorov, Danil V.; Sofeikov, Konstantin I. (2016). "Approximation with Random Bases: Pro et Contra". Information Sciences. 364–365: 129–145. arXiv:1506.04631. doi:10.1016/j.ins.2015.09.021. S2CID 2239376.
- ^ Artstein, Shiri (2002). "Proportional concentration phenomena of the sphere" (PDF). Israel Journal of Mathematics. 132 (1): 337–358. CiteSeerX 10.1.1.417.2375. doi:10.1007/BF02784520. S2CID 8095719.
- ^ Blass 1984
References
[edit]General references
[edit]- Blass, Andreas (1984), "Existence of bases implies the axiom of choice" (PDF), Axiomatic set theory, Contemporary Mathematics volume 31, Providence, R.I.: American Mathematical Society, pp. 31–33, ISBN 978-0-8218-5026-8, MR 0763890
- Brown, William A. (1991), Matrices and vector spaces, New York: M. Dekker, ISBN 978-0-8247-8419-5
- Lang, Serge (1987), Linear algebra, Berlin, New York: Springer-Verlag, ISBN 978-0-387-96412-6
Historical references
[edit]- Banach, Stefan (1922), "Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (On operations in abstract sets and their application to integral equations)" (PDF), Fundamenta Mathematicae (in French), 3: 133–181, doi:10.4064/fm-3-1-133-181, ISSN 0016-2736
- Bolzano, Bernard (1804), Betrachtungen über einige Gegenstände der Elementargeometrie (Considerations of some aspects of elementary geometry) (in German)
- Bourbaki, Nicolas (1969), Éléments d'histoire des mathématiques (Elements of history of mathematics) (in French), Paris: Hermann
- Dorier, Jean-Luc (1995), "A general outline of the genesis of vector space theory", Historia Mathematica, 22 (3): 227–261, doi:10.1006/hmat.1995.1024, MR 1347828
- Fourier, Jean Baptiste Joseph (1822), Théorie analytique de la chaleur (in French), Chez Firmin Didot, père et fils
- Grassmann, Hermann (1844), Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik (in German), reprint: Hermann Grassmann. Translated by Lloyd C. Kannenberg. (2000), Extension Theory, Kannenberg, L.C., Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-2031-5
- Hamel, Georg (1905), "Eine Basis aller Zahlen und die unstetigen Lösungen der Funktionalgleichung f(x+y)=f(x)+f(y)", Mathematische Annalen (in German), 60 (3), Leipzig: 459–462, doi:10.1007/BF01457624, S2CID 120063569
- Hamilton, William Rowan (1853), Lectures on Quaternions, Royal Irish Academy
- Möbius, August Ferdinand (1827), Der Barycentrische Calcul : ein neues Hülfsmittel zur analytischen Behandlung der Geometrie (Barycentric calculus: a new utility for an analytic treatment of geometry) (in German), archived from the original on 2009-04-12
- Moore, Gregory H. (1995), "The axiomatization of linear algebra: 1875–1940", Historia Mathematica, 22 (3): 262–303, doi:10.1006/hmat.1995.1025
- Peano, Giuseppe (1888), Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva (in Italian), Turin
{{citation}}: CS1 maint: location missing publisher (link)
External links
[edit]- Instructional videos from Khan Academy
- "Linear combinations, span, and basis vectors". Essence of linear algebra. August 6, 2016. Archived from the original on 2021-11-17 – via YouTube.
- "Basis", Encyclopedia of Mathematics, EMS Press, 2001 [1994]



























































