Mathematics desk
< July 25	<< Jun \| July \| Aug >>	July 27 >

Welcome to the Wikipedia Mathematics Reference Desk Archives
The page you are currently viewing is an archive page. While you can leave answers for any questions shown below, please ask new questions on one of the current reference desk pages.

July 26

Mathematical Economics / Game Theory: A proof that Dictatorship is the fairest form of government.

At Univeristy in an intermediate/advanced Mathematical Microeconmics course I learned a proof that the only "fair" form of government was a dictatorship.

It ran something along the lines of:

Establishing a set of "fairness" tests that seem intuitively reasonable. For example, if all members of a society want X to happen then X should happen.

Showing that these tests could only be satisfied by a dictatorship (not a democracy).

I cannot remember the name of the theory, so can't think of any other way to search for it. If someone reminds me of the name, I can look it up myself...

Thanks in advance.

192.193.1.5 06:29, 26 July 2007 (UTC)Glove_Man[reply]

The closest thing that comes to mind is Arrow's impossibility theorem. I don't know if that's quite it, but it sounds along those lines. - Rainwarrior 06:45, 26 July 2007 (UTC)[reply]

I agree this is probably what the OP has meant. It should be emphasized, though, that the theorem is very far from stating that dictatorship is the fairest form of government - for various reasons. One of them is that the "reasonable" requirements aren't all that reasonable - personally, I have a problem with the "independence of irrelevant alternatives" assumption. -- Meni Rosenfeld (talk) 14:41, 26 July 2007 (UTC)[reply]

Indeed, our article on Arrow's theorem gives the formulation "The only voting method that isn't flawed is a dictatorship". If the proof of this corollary is along the lines of: "No social welfare function on a set of three or more alternatives satifies the Arrow conditions; therefore, dictatorship is not flawed", then the "therefore" step could do with some elaboration. It is reminiscent of Euler's alleged existence proof of God. --Lambiam 19:00, 26 July 2007 (UTC)[reply]

I'd say the syllogism goes more like:

Major premise: A voting system that fails Arrow's conditions 2–5 is flawed.
Minor premise: The only voting system that can always satisfy Arrow's conditions 2–5 is dictatorship.
Conclusion: The only voting system that isn't flawed is dictatorship.

An unstated additional premise here, of course, is that dictatorship isn't per se flawed. Arrow's first condition specifically says it is, leading to the alternative conclusion that every voting system is flawed. —Ilmari Karonen (talk) 11:40, 27 July 2007 (UTC)[reply]

"independence of irrelevant alternatives" makes sense to me; the one that doesn't is the requirement that the algorithm provide a complete ranking of all possible outcomes, which is vastly more information than you need in most elections. Consider for example a board election with 30 candidates for 10 seats: why would you want an ordering of all 3E7 choices? —Tamfang 01:45, 30 July 2007 (UTC)[reply]

The simplest explanation for my doubt is this: Suppose there are two voters trying to order X, Y and Z. One votes X < Y < Z and the other Z < X < Y. In some intuitive way, Y seems to "do better" than Z. So I wouldn't be surprised if a "fair" way of combining the votes will give Z < Y. However, if we assume independence of irrelevant alternatives, then as far as Y and Z are concerned, this is the same as if the votes were Y < Z and Z < Y, so neither would have an advantage. -- Meni Rosenfeld (talk) 08:02, 30 July 2007 (UTC)[reply]

Oh well, I don't share your intuition! —Tamfang 09:09, 5 August 2007 (UTC)[reply]

Each of us is of course entitled to their own intuition, but I can't understand where your disagreement is coming from. Do you not agree that with votes X<Y<Z and Z<X<Y, Y is 1st place once and 2nd place once, Z is 1st place once and 3rd place once, and X is 2nd place once and 3rd place once? Do you not agree that 2nd is better than 3rd, and consequentially that Y has better votes than Z? And do you not agree, that under very reasonable assumptions on the underlying mechanism (for example, X, Y and Z have a "real" ordering, where each one of the voters has a greater than 1/2 probability of discovering the true relationship between each pair), conditioned on these votes, Y has a higher probability of being the top choice than Z? -- Meni Rosenfeld (talk) 12:18, 5 August 2007 (UTC)[reply]

Hm. Now that I've drawn the two sequences in columns, I see what you mean (it didn't jump out from the << notation). Yes, Y "does better" than Z if we can assume that the strengths of the preferences represented by "<" are all equal; but that assumption is arbitrary. —Tamfang 07:32, 6 August 2007 (UTC)[reply]

Indeed. But I think this, at the very least, demonstrates why the "ind. of irr. alt." axiom is not something which should be included without question. And I do think it is by far better to give that up than giving up non-dictatorship. -- Meni Rosenfeld (talk) 12:32, 6 August 2007 (UTC)[reply]

(shrug) My favored solution is to "give up" the habit of imposing one group's preferences on another. —Tamfang 18:37, 6 August 2007 (UTC)[reply]

Gomboc

I Got no answer on the misc page so i'm going to try here. Any idea where I could purchase a Gomboc from? preferably made from something durable like metal or glass. Capuchin 07:13, 25 July 2007 (UTC)[reply]

Did you try asking for information using the e-mail addresses info@gomboc·eu or domokos@iit·bme·hu given on the Gömböc homepage (http://www.gomboc.eu)? --Lambiam 15:34, 26 July 2007 (UTC)[reply]

I'm guessing its not going to be commercially available, it seems like they are only made from Rapid prototyping systems, so material choice is going to be limited. And you would probably have to sweettalk someone in an engenering department.

The linked article [1] is intrguing with many references to a Jacobi’s theorem which has many applications, and that always something had to be bigger or equal to four.. Our Jacobi's theorem disambig does not mention this, and it appears to be something related to the Four-vertex theorem. Anyone know more about this? --Salix alba (talk) 23:10, 26 July 2007 (UTC)[reply]

The Gomboc in the video on the homepage is what I would be looking for... I think I will see if my uni has a RPS that I could get some use out of ;) Capuchin 07:34, 27 July 2007 (UTC)[reply]

an intuitive reason for sine and cosine functions.

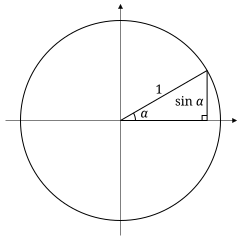
I understand the formal definition of a sine wave as EITHER returning "for each x, in a triangle with one of the angles being x, the ratio of the length of the side opposite of that angle to the length of the longest side" OR returning the Y value on a unit circle with an angle opened from the positive x axis, that number of degrees counterclockwise. But I don't get why these should be the same function. And I don't get intuitively why there's a reason the first definition should work for every triangle, no matter the lengths or what it looks like. (Triangles don't all look congruent!)

So my questions are: 1) why is "sine = opposite over hypotenuse" the same for EVERY triangle with one such angle in it, no matter what triangle I draw. If I start with an angle, say, 37 degrees, then I can draw infinite triangles which include angle. I just don't get as I draw all different kinds of triangles, why the ratio of their two sides (the opposite and the hypotenuse) should remain exactly the same! What wouldn't make sense if this weren't so? Or, from what does it follow that this has to be so? And secondly, what makes the Y value at the point on the unit circle that many degrees from the positive x axis counterclockwise the SAME????

Thank you!!!! - 84.0.158.245 22:30, 26 July 2007 (UTC)[reply]

The answer is similar triangles - in particular, any two triangles that have two angles in common are similar (in this case, the angle theta and the right angle - note that the trig functions are defined for right-angled triangles, not arbitrary ones), and so their corresponding sides are in the same ratio, and so the ratio of their sides is always the same. Then, for the other thing you considered, draw your line from the origin to the unit circle, then drop another line straight down from that point to the x-axis. You now have a right-angled triangle, with a hypotenuse of 1, and an opposite side equal to the y-value. That answer your question? Confusing Manifestation 22:50, 26 July 2007 (UTC)[reply]

Perhaps the illustration I've added on the right might help. Note that, for your rule to work as stated, the triangle has to be a right triangle; otherwise you'd need the general sine rule, which is more complicated. —Ilmari Karonen (talk) 11:14, 27 July 2007 (UTC)[reply]

The answer is very simple. It's called RATIO.

Imagine a right angle triangle. Imagine, you measure all the ratios of the three sides. Now imagine taking a picture of the triangle with a film 35mm camera.

Now here is the bit, imagine blowing up the picture,eh, I mean imagine increasing the size of the picture by developing the film. The RATIO is the same no matter how big (or how small) you make the picture.

This is why the Sine of a fixed angle is the same for all right angle triangles. 211.28.125.199 12:41, 27 July 2007 (UTC)[reply]

What's this formula?

[2] It's part of the Halo 3 Iris ARG in case you were wondering. 67.188.81.5 23:12, 26 July 2007 (UTC)[reply]

Cleaner version here [3] 67.188.81.5 23:24, 26 July 2007 (UTC)[reply]

i.e.

{\bar {\Psi _{0}}}={\sqrt {\frac {m}{\pi }}}e

—Tamfang 02:26, 30 July 2007 (UTC)[reply]

Psi has many possible meanings. m is often Mass. pi is usually 3.14159. e might be 2.71828 or the charge on an electron or just possibly energy. This looks like an equation from some branch of physics. -- SGBailey 08:41, 27 July 2007 (UTC)[reply]

Validity of the theory behind Elo ratings

From the Elo rating article:

If Player A has true strength

R_{A}

and Player B has true strength

R_{B}

, the exact formula (using the logistic curve) for the expected score of Player A is

E_{A}={\frac {1}{1+10^{(R_{B}-R_{A})/400}}}.

Similarly the expected score for Player B is

E_{B}={\frac {1}{1+10^{(R_{A}-R_{B})/400}}}.

How do we know this is the correct formula (i.e. that there is any set of R values across all players for which this formula will give the correct expected scores), even assuming that each player is just as likely to play black as white? (It takes for granted, for instance, that if E_{A vs B} = .80 and E_{B vs C} = .80 then E_{A vs C} = .94.) Somehow, I don't think the bookmaking industry (the ones who're directly interested in E) would accept it unquestioningly. Neon Merlin 23:25, 26 July 2007 (UTC)[reply]

Nobody, including Elo, believed the system was perfect. All validation and calibration has been based on observation. Although the principles have not changed, the current system is quite different in its details from the original one. While many people have attempted to further improve and refine the system, it is "good enough" for the FIDE to continue using it in its relatively simple form, while it has also found application for many other sports. The main purpose is and was not to serve as a predictor of expected scores, but just to assign a strength rating. The ratings are determined such that the values given by the formula conform to the observed probabilities that one player beats another. If the strength difference is so large that there is 80% chance that A will be beaten by B (an Elo rating difference of about 240 points), they will normally not be pitted against each other in a match, so this is outside the range for which we care anyway. --Lambiam 01:17, 27 July 2007 (UTC)[reply]

I'd say that this is not as much that the system is "good enough", as it is that FIDE is too lazy to do anything about it. My impression from looking at FIDE's implementation of the system is that it is very bad, and from an IM I know I have learnt that many proffesional players think so, too.

Though this doesn't matter in practice, it should be pointed out that FIDE's current implentation is based not on the logistic curve, but rather on the normal distribution. -- Meni Rosenfeld (talk) 10:48, 27 July 2007 (UTC)[reply]