Evolutionary algorithm: Difference between revisions
Restored revision 1107087915 by SimLibrarian (talk) |
Added a section with some points on the theoretical background of EAs. And a new sentence on the scope of Evolution Strategy. Tag: Disambiguation links added |
||
| Line 24: | Line 24: | ||
*[[Genetic programming]] – Here the solutions are in the form of computer programs, and their fitness is determined by their ability to solve a computational problem. There are many variants of Genetic Programming, including [[Cartesian genetic programming]], [[gene expression programming]], [[grammatical evolution]], [[linear genetic programming]], [[multi expression programming]] etc. |
*[[Genetic programming]] – Here the solutions are in the form of computer programs, and their fitness is determined by their ability to solve a computational problem. There are many variants of Genetic Programming, including [[Cartesian genetic programming]], [[gene expression programming]], [[grammatical evolution]], [[linear genetic programming]], [[multi expression programming]] etc. |
||
*[[Evolutionary programming]] – Similar to genetic programming, but the structure of the program is fixed and its numerical parameters are allowed to evolve. |
*[[Evolutionary programming]] – Similar to genetic programming, but the structure of the program is fixed and its numerical parameters are allowed to evolve. |
||
*[[Evolution strategy]] – Works with vectors of real numbers as representations of solutions, and typically uses self-adaptive mutation rates. The method is mainly used for numerical optimization, although there are also variants for combinatorial tasks.<ref>{{Citation |last=Nissen |first=Volker |last2=Krause |first2=Matthias |date=1994 |editor-last=Reusch |editor-first=Bernd |title=Constrained Combinatorial Optimization with an Evolution Strategy |url=https://link.springer.com/chapter/10.1007/978-3-642-79386-8_5 |journal=Fuzzy Logik |language=en |location=Berlin, Heidelberg |publisher=Springer |pages=33–40 |doi=10.1007/978-3-642-79386-8_5 |isbn=978-3-642-79386-8}}</ref><ref>{{Cite journal |last=Coelho |first=V. N. |last2=Coelho |first2=I. M. |last3=Souza |first3=M. J. F. |last4=Oliveira |first4=T. A. |last5=Cota |first5=L. P. |last6=Haddad |first6=M. N. |last7=Mladenovic |first7=N. |last8=Silva |first8=R. C. P. |last9=Guimarães |first9=F. G. |year=2016 |title=Hybrid Self-Adaptive Evolution Strategies Guided by Neighborhood Structures for Combinatorial Optimization Problems. |journal=Evol Comput |publication-date= |volume=24 |issue=4 |pages=637–666 |doi=10.1162/EVCO_a_00187}}</ref> |
|||
*[[Evolution strategy]] – Works with vectors of real numbers as representations of solutions, and typically uses self-adaptive mutation rates. |
|||
*[[Differential evolution]] – Based on vector differences and is therefore primarily suited for [[numerical optimization]] problems. |
*[[Differential evolution]] – Based on vector differences and is therefore primarily suited for [[numerical optimization]] problems. |
||
*[[Neuroevolution]] – Similar to genetic programming but the genomes represent artificial neural networks by describing structure and connection weights. The genome encoding can be direct or indirect. |
*[[Neuroevolution]] – Similar to genetic programming but the genomes represent artificial neural networks by describing structure and connection weights. The genome encoding can be direct or indirect. |
||
*[[Learning classifier system]] – Here the solution is a set of classifiers (rules or conditions). A Michigan-LCS evolves at the level of individual classifiers whereas a Pittsburgh-LCS uses populations of classifier-sets. Initially, classifiers were only binary, but now include real, neural net, or [[S-expression]] types. Fitness is typically determined with either a strength or accuracy based [[reinforcement learning]] or [[supervised learning]] approach. |
*[[Learning classifier system]] – Here the solution is a set of classifiers (rules or conditions). A Michigan-LCS evolves at the level of individual classifiers whereas a Pittsburgh-LCS uses populations of classifier-sets. Initially, classifiers were only binary, but now include real, neural net, or [[S-expression]] types. Fitness is typically determined with either a strength or accuracy based [[reinforcement learning]] or [[supervised learning]] approach. |
||
== Theoretical background == |
|||
The following theoretical principles apply to all or almost all EAs. |
|||
=== No free lunch theorem === |
|||
The [[no free lunch theorem]] of optimization states that all optimization strategies are equally effective when the set of all optimization problems is considered. Under the same condition, no evolutionary algorithm is fundamentally better than another. This can only be the case if the set of all problems is restricted. This is exactly what is inevitably done in practice. Therefore, to improve an EA, it must exploit problem knowledge in some form (e.g. by choosing a certain mutation strength or a [[Genetic representation|problem-adapted coding]]). Thus, if two EAs are compared, this constraint is implied. In addition, an EA can use problem specific knowledge by, for example, not randomly generating the entire start population, but creating some individuals through [[Heuristic (computer science)|heuristics]] or other procedures.<ref name="Davis91">{{Cite book |last=Davis |first=Lawrence |url=https://www.worldcat.org/oclc/23081440 |title=Handbook of genetic algorithms |date=1991 |publisher=Van Nostrand Reinhold |others= |isbn=0-442-00173-8 |location=New York |oclc=23081440}}</ref><ref>{{Citation |last=Lienig |first=Jens |title=An evolutionary algorithm for the routing of multi-chip modules |date=1994 |url=http://link.springer.com/10.1007/3-540-58484-6_301 |work=Parallel Problem Solving from Nature — PPSN III |volume=866 |pages=588–597 |editor-last=Davidor |editor-first=Yuval |place=Berlin, Heidelberg |publisher=Springer |doi=10.1007/3-540-58484-6_301 |isbn=978-3-540-58484-1 |access-date=2022-10-18 |last2=Brandt |first2=Holger |editor2-last=Schwefel |editor2-first=Hans-Paul |editor3-last=Männer |editor3-first=Reinhard}}</ref> Another possibility to tailor an EA to a given problem domain is to involve suitable heuristics, [[Local search (optimization)|local search procedures]] or other problem-related procedures in the process of generating the offspring. This form of extension of an EA is also known as a [[memetic algorithm]]. Both extensions play a major role in practical applications, as they can speed up the search process and make it more robust.<ref name="Davis91" /><ref>{{Cite book |url=http://link.springer.com/10.1007/978-3-642-23247-3 |title=Handbook of Memetic Algorithms |date=2012 |publisher=Springer Berlin Heidelberg |isbn=978-3-642-23246-6 |editor-last=Neri |editor-first=Ferrante |series=Studies in Computational Intelligence |volume=379 |location=Berlin, Heidelberg |language=en |doi=10.1007/978-3-642-23247-3 |editor-last2=Cotta |editor-first2=Carlos |editor-last3=Moscato |editor-first3=Pablo}}</ref> |
|||
=== Convergence === |
|||
For EAs in which, in addition to the offspring, at least the best individual of the parent generation is used to form the subsequent generation (so-called elitist EAs), there is a general proof of [[Convergence#Mathematics|convergence]] under the condition that an [[optimum]] exists. [[Without loss of generality]], a maximum search is assumed for the proof: |
|||
From the property of elitist offspring acceptance and the existance of the optimum it follows that per generation <math>k</math> an improvement of the fitness <math>F</math> of the respective best individual <math>x'</math> will occur with a probability <math>P > 0</math>. Thus: |
|||
:<math>F(x'_1) \leq F(x'_2) \leq F(x'_3) \leq \cdots \leq F(x'_k) \leq \cdots</math> |
|||
I.e., the fitness values represent a [[Monotonic function|monotonically]] non-decreasing [[sequence]], which is [[bounded set|bounded]] due to the existence of the optimum. From this follows the convergence of the sequence against the optimum. |
|||
Since the proof makes no statement about the speed of convergence, it is of little help in practical applications of EAs. But it does justify the recommendation to use elitist EAs. However, when using the usual [[Panmixia|panmictic]] population model, elitist EAs tend to [[Premature convergence|converge prematurely]] more than non-elitist ones. In a panmictic population model, mate selection (step 2 of the section about implementation) is such that every individual in the entire population is eligible as a mate. In non-panmictic populations, selection is suitably restricted, so that the dispersal speed of better individuals is reduced compared to panmictic ones. Thus, the general risk of premature convergence of elitist EAs can be significantly reduced by suitable population models that restrict mate selection.<ref>{{Citation |last=Gorges-Schleuter |first=Martina |title=A comparative study of global and local selection in evolution strategies |date=1998 |url=http://link.springer.com/10.1007/BFb0056879 |work=Parallel Problem Solving from Nature — PPSN V |volume=1498 |pages=367–377 |editor-last=Eiben |editor-first=Agoston E. |place=Berlin, Heidelberg |publisher=Springer Berlin Heidelberg |doi=10.1007/bfb0056879 |isbn=978-3-540-65078-2 |access-date=2022-10-21 |editor2-last=Bäck |editor2-first=Thomas |editor3-last=Schoenauer |editor3-first=Marc |editor4-last=Schwefel |editor4-first=Hans-Paul}}</ref><ref>{{Cite book |last=Dorronsoro |first=Bernabe |url=http://link.springer.com/10.1007/978-0-387-77610-1 |title=Cellular Genetic Algorithms |last2=Alba |first2=Enrique |date=2008 |publisher=Springer US |isbn=978-0-387-77609-5 |series=Operations Research/Computer Science Interfaces Series |volume=42 |location=Boston, MA |doi=10.1007/978-0-387-77610-1}}</ref> |
|||
=== Virtual Alphabets === |
|||
With the theory of virtual alphabets, [[David E. Goldberg]] showed in 1990 that by using a representation with real numbers, an EA that uses classical [[Crossover (genetic algorithm)|recombination operators]] (e.g. uniform or n-point crossover) cannot reach certain areas of the search space, in contrast to a coding with binary numbers.<ref>{{Citation |last=Goldberg |first=David E. |title=The theory of virtual alphabets |date=1990 |url=http://link.springer.com/10.1007/BFb0029726 |work=Parallel Problem Solving from Nature |volume=496 |pages=13–22 |publication-date=1991 |editor-last=Schwefel |editor-first=Hans-Paul |place=Berlin/Heidelberg |publisher=Springer-Verlag |language=en |doi=10.1007/bfb0029726 |isbn=978-3-540-54148-6 |access-date=2022-10-22 |editor2-last=Männer |editor2-first=Reinhard}}</ref> This results in the recommendation for EAs with real representation to use arithmetic operators for recombination (e.g. arithmetic mean or intermediate recombination). With suitable operators, real-valued representations are more effective than binary ones, contrary to earlier opinion.<ref>{{Cite book |last=Stender |first=J. |url=https://www.worldcat.org/oclc/47216370 |title=Genetic algorithms in optimisation, simulation, and modelling |last2=Hillebrand |first2=E. |last3=Kingdon |first3=J. |date=1994 |publisher=IOS Press |others= |isbn=90-5199-180-0 |location=Amsterdam |oclc=47216370}}</ref><ref>{{Cite book |last=Michalewicz |first=Zbigniew |url=https://www.worldcat.org/oclc/851375253 |title=Genetic Algorithms + Data Structures = Evolution Programs |date=1996 |publisher=Springer |isbn=978-3-662-03315-9 |edition=3rd |publication-place=Berlin Heidelberg |oclc=851375253}}</ref> |
|||
==Comparison to biological processes== |
==Comparison to biological processes== |
||
Revision as of 14:54, 25 October 2022
| Part of a series on |
| Artificial intelligence |
|---|
In computational intelligence (CI), an evolutionary algorithm (EA) is a subset of evolutionary computation,[1] a generic population-based metaheuristic optimization algorithm. An EA uses mechanisms inspired by biological evolution, such as reproduction, mutation, recombination, and selection. Candidate solutions to the optimization problem play the role of individuals in a population, and the fitness function determines the quality of the solutions (see also loss function). Evolution of the population then takes place after the repeated application of the above operators.
Evolutionary algorithms often perform well approximating solutions to all types of problems because they ideally do not make any assumption about the underlying fitness landscape. Techniques from evolutionary algorithms applied to the modeling of biological evolution are generally limited to explorations of microevolutionary processes and planning models based upon cellular processes. In most real applications of EAs, computational complexity is a prohibiting factor.[2] In fact, this computational complexity is due to fitness function evaluation. Fitness approximation is one of the solutions to overcome this difficulty. However, seemingly simple EA can solve often complex problems;[citation needed] therefore, there may be no direct link between algorithm complexity and problem complexity.
Implementation
The following is an example of a generic single-objective genetic algorithm.
Step One: Generate the initial population of individuals randomly. (First generation)
Step Two: Repeat the following regenerational steps until termination:
- Evaluate the fitness of each individual in the population (time limit, sufficient fitness achieved, etc.)
- Select the fittest individuals for reproduction. (Parents)
- Breed new individuals through crossover and mutation operations to give birth to offspring.
- Replace the least-fit individuals of the population with new individuals.
Types
Similar techniques differ in genetic representation and other implementation details, and the nature of the particular applied problem.
- Genetic algorithm – This is the most popular type of EA. One seeks the solution of a problem in the form of strings of numbers (traditionally binary, although the best representations are usually those that reflect something about the problem being solved),[2] by applying operators such as recombination and mutation (sometimes one, sometimes both). This type of EA is often used in optimization problems.
- Genetic programming – Here the solutions are in the form of computer programs, and their fitness is determined by their ability to solve a computational problem. There are many variants of Genetic Programming, including Cartesian genetic programming, gene expression programming, grammatical evolution, linear genetic programming, multi expression programming etc.
- Evolutionary programming – Similar to genetic programming, but the structure of the program is fixed and its numerical parameters are allowed to evolve.
- Evolution strategy – Works with vectors of real numbers as representations of solutions, and typically uses self-adaptive mutation rates. The method is mainly used for numerical optimization, although there are also variants for combinatorial tasks.[3][4]
- Differential evolution – Based on vector differences and is therefore primarily suited for numerical optimization problems.
- Neuroevolution – Similar to genetic programming but the genomes represent artificial neural networks by describing structure and connection weights. The genome encoding can be direct or indirect.
- Learning classifier system – Here the solution is a set of classifiers (rules or conditions). A Michigan-LCS evolves at the level of individual classifiers whereas a Pittsburgh-LCS uses populations of classifier-sets. Initially, classifiers were only binary, but now include real, neural net, or S-expression types. Fitness is typically determined with either a strength or accuracy based reinforcement learning or supervised learning approach.
Theoretical background
The following theoretical principles apply to all or almost all EAs.
No free lunch theorem
The no free lunch theorem of optimization states that all optimization strategies are equally effective when the set of all optimization problems is considered. Under the same condition, no evolutionary algorithm is fundamentally better than another. This can only be the case if the set of all problems is restricted. This is exactly what is inevitably done in practice. Therefore, to improve an EA, it must exploit problem knowledge in some form (e.g. by choosing a certain mutation strength or a problem-adapted coding). Thus, if two EAs are compared, this constraint is implied. In addition, an EA can use problem specific knowledge by, for example, not randomly generating the entire start population, but creating some individuals through heuristics or other procedures.[5][6] Another possibility to tailor an EA to a given problem domain is to involve suitable heuristics, local search procedures or other problem-related procedures in the process of generating the offspring. This form of extension of an EA is also known as a memetic algorithm. Both extensions play a major role in practical applications, as they can speed up the search process and make it more robust.[5][7]
Convergence
For EAs in which, in addition to the offspring, at least the best individual of the parent generation is used to form the subsequent generation (so-called elitist EAs), there is a general proof of convergence under the condition that an optimum exists. Without loss of generality, a maximum search is assumed for the proof:
From the property of elitist offspring acceptance and the existance of the optimum it follows that per generation an improvement of the fitness of the respective best individual will occur with a probability . Thus:
I.e., the fitness values represent a monotonically non-decreasing sequence, which is bounded due to the existence of the optimum. From this follows the convergence of the sequence against the optimum.
Since the proof makes no statement about the speed of convergence, it is of little help in practical applications of EAs. But it does justify the recommendation to use elitist EAs. However, when using the usual panmictic population model, elitist EAs tend to converge prematurely more than non-elitist ones. In a panmictic population model, mate selection (step 2 of the section about implementation) is such that every individual in the entire population is eligible as a mate. In non-panmictic populations, selection is suitably restricted, so that the dispersal speed of better individuals is reduced compared to panmictic ones. Thus, the general risk of premature convergence of elitist EAs can be significantly reduced by suitable population models that restrict mate selection.[8][9]
Virtual Alphabets
With the theory of virtual alphabets, David E. Goldberg showed in 1990 that by using a representation with real numbers, an EA that uses classical recombination operators (e.g. uniform or n-point crossover) cannot reach certain areas of the search space, in contrast to a coding with binary numbers.[10] This results in the recommendation for EAs with real representation to use arithmetic operators for recombination (e.g. arithmetic mean or intermediate recombination). With suitable operators, real-valued representations are more effective than binary ones, contrary to earlier opinion.[11][12]
Comparison to biological processes
A possible limitation[according to whom?] of many evolutionary algorithms is their lack of a clear genotype–phenotype distinction. In nature, the fertilized egg cell undergoes a complex process known as embryogenesis to become a mature phenotype. This indirect encoding is believed to make the genetic search more robust (i.e. reduce the probability of fatal mutations), and also may improve the evolvability of the organism.[13][14] Such indirect (also known as generative or developmental) encodings also enable evolution to exploit the regularity in the environment.[15] Recent work in the field of artificial embryogeny, or artificial developmental systems, seeks to address these concerns. And gene expression programming successfully explores a genotype–phenotype system, where the genotype consists of linear multigenic chromosomes of fixed length and the phenotype consists of multiple expression trees or computer programs of different sizes and shapes.[16][improper synthesis?]
Related techniques
Swarm algorithms[clarification needed] include:
- Ant colony optimization is based on the ideas of ant foraging by pheromone communication to form paths.[17] Primarily suited for combinatorial optimization and graph problems.
- The runner-root algorithm (RRA) is inspired by the function of runners and roots of plants in nature.[18]
- Artificial bee colony algorithm is based on the honey bee foraging behaviour. Primarily proposed for numerical optimization and extended to solve combinatorial, constrained and multi-objective optimization problems.
- Bees algorithm is based on the foraging behaviour of honey bees. It has been applied in many applications such as routing and scheduling.
- Cuckoo search is inspired by the brooding parasitism of the cuckoo species. It also uses Lévy flights, and thus it suits for global optimization problems.
- Particle swarm optimization is based on the ideas of animal flocking behaviour.[17] Also primarily suited for numerical optimization problems.
Other population-based metaheuristic methods
- Hunting Search – A method inspired by the group hunting of some animals such as wolves that organize their position to surround the prey, each of them relative to the position of the others and especially that of their leader. It is a continuous optimization method[19] adapted as a combinatorial optimization method.[20]
- Adaptive dimensional search – Unlike nature-inspired metaheuristic techniques, an adaptive dimensional search algorithm does not implement any metaphor as an underlying principle. Rather it uses a simple performance-oriented method, based on the update of the search dimensionality ratio (SDR) parameter at each iteration.[21]
- Firefly algorithm is inspired by the behavior of fireflies, attracting each other by flashing light. This is especially useful for multimodal optimization.
- Harmony search – Based on the ideas of musicians' behavior in searching for better harmonies. This algorithm is suitable for combinatorial optimization as well as parameter optimization.
- Gaussian adaptation – Based on information theory. Used for maximization of manufacturing yield, mean fitness or average information. See for instance Entropy in thermodynamics and information theory.
- Memetic algorithm – A hybrid method, inspired by Richard Dawkins's notion of a meme, it commonly takes the form of a population-based algorithm coupled with individual learning procedures capable of performing local refinements. Emphasizes the exploitation of problem-specific knowledge, and tries to orchestrate local and global search in a synergistic way.
Examples
In 2020, Google stated that their AutoML-Zero can successfully rediscover classic algorithms such as the concept of neural networks.[22]
The computer simulations Tierra and Avida attempt to model macroevolutionary dynamics.
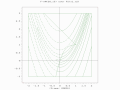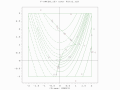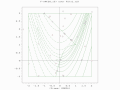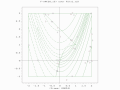
Gallery
-
A two-population EA search over a constrained Rosenbrock function with bounded global optimum
-
A two-population EA search over a constrained Rosenbrock function. Global optimum is not bounded.
-
A two-population EA search of a bounded optima of Simionescu's function
References
- ^ Vikhar, P. A. (2016). "Evolutionary algorithms: A critical review and its future prospects". Proceedings of the 2016 International Conference on Global Trends in Signal Processing, Information Computing and Communication (ICGTSPICC). Jalgaon: 261–265. doi:10.1109/ICGTSPICC.2016.7955308. ISBN 978-1-5090-0467-6. S2CID 22100336.
- ^ a b Cohoon, J; et al. (2002-11-26). Evolutionary algorithms for the physical design of VLSI circuits (PDF). Springer, pp. 683-712, 2003. ISBN 978-3-540-43330-9.
{{cite book}}:|journal=ignored (help) - ^ Nissen, Volker; Krause, Matthias (1994), Reusch, Bernd (ed.), "Constrained Combinatorial Optimization with an Evolution Strategy", Fuzzy Logik, Berlin, Heidelberg: Springer: 33–40, doi:10.1007/978-3-642-79386-8_5, ISBN 978-3-642-79386-8
- ^ Coelho, V. N.; Coelho, I. M.; Souza, M. J. F.; Oliveira, T. A.; Cota, L. P.; Haddad, M. N.; Mladenovic, N.; Silva, R. C. P.; Guimarães, F. G. (2016). "Hybrid Self-Adaptive Evolution Strategies Guided by Neighborhood Structures for Combinatorial Optimization Problems". Evol Comput. 24 (4): 637–666. doi:10.1162/EVCO_a_00187.
- ^ a b Davis, Lawrence (1991). Handbook of genetic algorithms. New York: Van Nostrand Reinhold. ISBN 0-442-00173-8. OCLC 23081440.
- ^ Lienig, Jens; Brandt, Holger (1994), Davidor, Yuval; Schwefel, Hans-Paul; Männer, Reinhard (eds.), "An evolutionary algorithm for the routing of multi-chip modules", Parallel Problem Solving from Nature — PPSN III, vol. 866, Berlin, Heidelberg: Springer, pp. 588–597, doi:10.1007/3-540-58484-6_301, ISBN 978-3-540-58484-1, retrieved 2022-10-18
- ^ Neri, Ferrante; Cotta, Carlos; Moscato, Pablo, eds. (2012). Handbook of Memetic Algorithms. Studies in Computational Intelligence. Vol. 379. Berlin, Heidelberg: Springer Berlin Heidelberg. doi:10.1007/978-3-642-23247-3. ISBN 978-3-642-23246-6.
- ^ Gorges-Schleuter, Martina (1998), Eiben, Agoston E.; Bäck, Thomas; Schoenauer, Marc; Schwefel, Hans-Paul (eds.), "A comparative study of global and local selection in evolution strategies", Parallel Problem Solving from Nature — PPSN V, vol. 1498, Berlin, Heidelberg: Springer Berlin Heidelberg, pp. 367–377, doi:10.1007/bfb0056879, ISBN 978-3-540-65078-2, retrieved 2022-10-21
- ^ Dorronsoro, Bernabe; Alba, Enrique (2008). Cellular Genetic Algorithms. Operations Research/Computer Science Interfaces Series. Vol. 42. Boston, MA: Springer US. doi:10.1007/978-0-387-77610-1. ISBN 978-0-387-77609-5.
- ^ Goldberg, David E. (1990), Schwefel, Hans-Paul; Männer, Reinhard (eds.), "The theory of virtual alphabets", Parallel Problem Solving from Nature, vol. 496, Berlin/Heidelberg: Springer-Verlag (published 1991), pp. 13–22, doi:10.1007/bfb0029726, ISBN 978-3-540-54148-6, retrieved 2022-10-22
- ^ Stender, J.; Hillebrand, E.; Kingdon, J. (1994). Genetic algorithms in optimisation, simulation, and modelling. Amsterdam: IOS Press. ISBN 90-5199-180-0. OCLC 47216370.
- ^ Michalewicz, Zbigniew (1996). Genetic Algorithms + Data Structures = Evolution Programs (3rd ed.). Berlin Heidelberg: Springer. ISBN 978-3-662-03315-9. OCLC 851375253.
- ^ G.S. Hornby and J.B. Pollack. "Creating high-level components with a generative representation for body-brain evolution". Artificial Life, 8(3):223–246, 2002.
- ^ Jeff Clune, Benjamin Beckmann, Charles Ofria, and Robert Pennock. "Evolving Coordinated Quadruped Gaits with the HyperNEAT Generative Encoding" Archived 2016-06-03 at the Wayback Machine. Proceedings of the IEEE Congress on Evolutionary Computing Special Section on Evolutionary Robotics, 2009. Trondheim, Norway.
- ^ J. Clune, C. Ofria, and R. T. Pennock, "How a generative encoding fares as problem-regularity decreases", in PPSN (G. Rudolph, T. Jansen, S. M. Lucas, C. Poloni, and N. Beume, eds.), vol. 5199 of Lecture Notes in Computer Science, pp. 358–367, Springer, 2008.
- ^ Ferreira, C., 2001. "Gene Expression Programming: A New Adaptive Algorithm for Solving Problems". Complex Systems, Vol. 13, issue 2: 87–129.
- ^ a b Slowik, Adam; Kwasnicka, Halina (2018). "Nature Inspired Methods and Their Industry Applications—Swarm Intelligence Algorithms". IEEE Transactions on Industrial Informatics. 14 (3). Institute of Electrical and Electronics Engineers (IEEE): 1004–1015. doi:10.1109/tii.2017.2786782. ISSN 1551-3203. S2CID 3707290.
- ^ F. Merrikh-Bayat, "The runner-root algorithm: A metaheuristic for solving unimodal and multimodal optimization problems inspired by runners and roots of plants in nature", Applied Soft Computing, Vol. 33, pp. 292–303, 2015
- ^ Oftadeh, R.; Mahjoob, M.J.; Shariatpanahi, M. (October 2010). "A novel meta-heuristic optimization algorithm inspired by group hunting of animals: Hunting search". Computers & Mathematics with Applications. 60 (7): 2087–2098. doi:10.1016/j.camwa.2010.07.049.
- ^ Amine Agharghor; Mohammed Essaid Riffi (2017). "First Adaptation of Hunting Search Algorithm for the Quadratic Assignment Problem". Europe and MENA Cooperation Advances in Information and Communication Technologies. Advances in Intelligent Systems and Computing. 520: 263–267. doi:10.1007/978-3-319-46568-5_27. ISBN 978-3-319-46567-8.
- ^ Hasançebi, O., Kazemzadeh Azad, S. (2015), "Adaptive Dimensional Search: A New Metaheuristic Algorithm for Discrete Truss Sizing Optimization", Computers and Structures, 154, 1–16.
- ^ Gent, Edd (13 April 2020). "Artificial intelligence is evolving all by itself". Science | AAAS. Archived from the original on 16 April 2020. Retrieved 16 April 2020.
- ^ Simionescu, P.A.; Beale, D.G.; Dozier, G.V. (2004). "Constrained optimization problem solving using estimation of distribution algorithms" (PDF). Proc. of the 2004 Congress on Evolutionary Computation - CEC2004. Portland, OR: 1647–1653. doi:10.1109/CEC.2006.1688506. S2CID 1717817. Retrieved 7 January 2017.
{{cite journal}}: Cite journal requires|journal=(help) - ^ Simionescu, P.A.; Dozier, G.V.; Wainwright, R.L. (2006). "A Two-Population Evolutionary Algorithm for Constrained Optimization Problems" (PDF). 2006 IEEE International Conference on Evolutionary Computation. Proc 2006 IEEE International Conference on Evolutionary Computation. Vancouver, Canada. pp. 1647–1653. doi:10.1109/CEC.2006.1688506. ISBN 0-7803-9487-9. S2CID 1717817. Retrieved 7 January 2017.
{{cite book}}: CS1 maint: location missing publisher (link) - ^ Simionescu, P.A. (2014). Computer Aided Graphing and Simulation Tools for AutoCAD Users (1st ed.). Boca Raton, FL: CRC Press. ISBN 978-1-4822-5290-3.
External links
Bibliography
- Ashlock, D. (2006), Evolutionary Computation for Modeling and Optimization, Springer, ISBN 0-387-22196-4.
- Bäck, T. (1996), Evolutionary Algorithms in Theory and Practice: Evolution Strategies, Evolutionary Programming, Genetic Algorithms, Oxford Univ. Press.
- Bäck, T., Fogel, D., Michalewicz, Z. (1997), Handbook of Evolutionary Computation, Oxford Univ. Press.
- Banzhaf, W., Nordin, P., Keller, R., Francone, F. (1998), Genetic Programming - An Introduction, Morgan Kaufmann, San Francisco
- Eiben, A.E., Smith, J.E. (2003), Introduction to Evolutionary Computing, Springer.
- Holland, J. H. (1992), Adaptation in Natural and Artificial Systems, The University of Michigan Press, Ann Arbor
- Michalewicz Z., Fogel D.B. (2004). How To Solve It: Modern Heuristics, Springer.
- Benko, Attila; Dosa, Gyorgy; Tuza, Zsolt (2010). "Bin Packing/Covering with Delivery, solved with the evolution of algorithms". 2010 IEEE Fifth International Conference on Bio-Inspired Computing: Theories and Applications (BIC-TA). pp. 298–302. doi:10.1109/BICTA.2010.5645312. ISBN 978-1-4244-6437-1. S2CID 16875144.
- Poli, R.; Langdon, W. B.; McPhee, N. F. (2008). A Field Guide to Genetic Programming. Lulu.com, freely available from the internet. ISBN 978-1-4092-0073-4. Archived from the original on 2016-05-27. Retrieved 2011-03-05.[self-published source]
- Price, K., Storn, R.M., Lampinen, J.A., (2005). "Differential Evolution: A Practical Approach to Global Optimization", Springer.
- Ingo Rechenberg (1971): Evolutionsstrategie - Optimierung technischer Systeme nach Prinzipien der biologischen Evolution (PhD thesis). Reprinted by Fromman-Holzboog (1973).
- Hans-Paul Schwefel (1974): Numerische Optimierung von Computer-Modellen (PhD thesis). Reprinted by Birkhäuser (1977).
- Simon, D. (2013): Evolutionary Optimization Algorithms, Wiley.
- Computational Intelligence: A Methodological Introduction by Kruse, Borgelt, Klawonn, Moewes, Steinbrecher, Held, 2013, Springer, ISBN 978-1-4471-5012-1
- Rahman, Rosshairy Abd.; Kendall, Graham; Ramli, Razamin; Jamari, Zainoddin; Ku-Mahamud, Ku Ruhana (2017). "Shrimp Feed Formulation via Evolutionary Algorithm with Power Heuristics for Handling Constraints". Complexity. 2017: 1–12. doi:10.1155/2017/7053710.