Pentagonal bipyramid: Difference between revisions

Pentagonal bipyramid
Pentagonal bipyramid
Type	Bipyramid,; Johnson; J12 – J13 – J14
Faces	10 triangles
Edges	15
Vertices	7
Vertex configuration	V4.4.5
Schläfli symbol	{ } + {5}
Coxeter diagram
Symmetry group	D5h, [5,2], (*225), order 20
Rotation group	D5, [5,2]+, (225), order 10
Dual polyhedron	pentagonal prism
Properties	convex, face-transitive, (deltahedron)
Net

Browse history interactively

← Previous edit Next edit →

Content deleted Content added

VisualWikitext

Inline

Revision as of 06:21, 7 March 2024

In geometry, the pentagonal bipyramid (or dipyramid) is third of the infinite set of face-transitive bipyramids, and the 13th Johnson solid ( $J 13$ ). Each bipyramid is the dual of a uniform prism.

Although it is face-transitive, it is not a Platonic solid because some vertices have four faces meeting and others have five faces.

Construction

Like other bipyramids, the pentagonal bipyramid can be constructed by attaching the base of two pentagonal pyramids. These pyramids cover their pentagonal base, such that the resulting polyhedron has 10 triangles as its faces.^[1] The pentagonal bipyramid is said to be right if the pyramids are symmetrically regular and both of their apices are on the line passing through the base's center; otherwise, it is oblique. If the pyramids are regular, then all edges of the triangular bipyramid are equal in length, making up the faces equilateral triangles. A polyhedron with only equilateral triangles as faces is called a deltahedron. There are only eight different convex deltahedra, one of which is the pentagonal bipyramid with regular faces. More generally, the convex polyhedron in which all faces are regular is the Johnson solid, and every convex deltahedra is a Johnson solid. The pentagonal bipyramid with the regular faces is among numbered the Johnson solids as $J_{13}$ , the thirteenth Johnson solid.^[2]

Properties

The pentagonal dipyramid is 4-connected, meaning that it takes the removal of four vertices to disconnect the remaining vertices. It is one of only four 4-connected simplicial well-covered polyhedra, meaning that all of the maximal independent sets of its vertices have the same size. The other three polyhedra with this property are the regular octahedron, the snub disphenoid, and an irregular polyhedron with 12 vertices and 20 triangular faces.^[3]

Formulae

The following formulae for the height ( $H$ ), surface area ( $A$ ) and volume ( $V$ ) can be used if all faces are regular, with edge length $L$ :^[4]

H=L\cdot {\sqrt {2-{\frac {2}{\sqrt {5}}}}}\approx L\cdot 1.0514622242

A=L^{2}\cdot {\frac {5{\sqrt {3}}}{2}}\approx L^{2}\cdot 4.330127019

V=L^{3}\cdot {\frac {5+{\sqrt {5}}}{12}}\approx L^{3}\cdot 0.6030056648

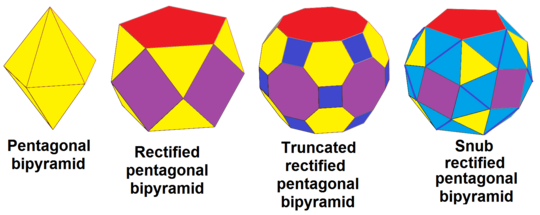
Related polyhedra

The pentagonal bipyramid, dt{2,5}, can be in sequence rectified, rdt{2,5}, truncated, trdt{2,5} and alternated (snubbed), srdt{2,5}:

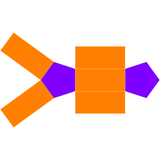
The dual of the Johnson solid pentagonal bipyramid is the pentagonal prism, with 7 faces: 5 rectangular faces and 2 pentagons.

Dual pentagonal bipyramid	Net of dual

References

^ Trigg, Charles W. (1978). "An infinite class of deltahedra". Mathematics Magazine. 51 (1): 55–57. doi:10.1080/0025570X.1978.11976675. JSTOR 2689647. MR 1572246.
^ Uehara, Ryuhei (2020). Introduction to Computational Origami: The World of New Computational Geometry. Springer. doi:10.1007/978-981-15-4470-5. ISBN 978-981-15-4470-5. S2CID 220150682.
^ Finbow, Arthur S.; Hartnell, Bert L.; Nowakowski, Richard J.; Plummer, Michael D. (2010), "On well-covered triangulations. III", Discrete Applied Mathematics, 158 (8): 894–912, doi:10.1016/j.dam.2009.08.002, MR 2602814.
^ Sapiña, R. "Area and volume of the Johnson solid J₁₃". Problemas y ecuaciones (in Spanish). ISSN 2659-9899. Retrieved 2020-09-04.

External links

Weisstein, Eric W., "Pentagonal dipyramid" ("Dipyramid") at MathWorld.
Conway Notation for Polyhedra Try: dP5

[trigg-1] Trigg, Charles W. (1978). "An infinite class of deltahedra". Mathematics Magazine. 51 (1): 55–57. doi:10.1080/0025570X.1978.11976675. JSTOR 2689647. MR 1572246.

[uehara-2] Uehara, Ryuhei (2020). Introduction to Computational Origami: The World of New Computational Geometry. Springer. doi:10.1007/978-981-15-4470-5. ISBN 978-981-15-4470-5. S2CID 220150682.

[3] Finbow, Arthur S.; Hartnell, Bert L.; Nowakowski, Richard J.; Plummer, Michael D. (2010), "On well-covered triangulations. III", Discrete Applied Mathematics, 158 (8): 894–912, doi:10.1016/j.dam.2009.08.002, MR 2602814.

[pye-4] Sapiña, R. "Area and volume of the Johnson solid J₁₃". Problemas y ecuaciones (in Spanish). ISSN 2659-9899. Retrieved 2020-09-04.

[1]

[2]

[3]

[4]

@@ Line 24: / Line 24: @@
 == Construction ==
-Like other bipyramids, the pentagonal bipyramid can be constructed by attaching the base of two pentagonal pyramids. These pyramids cover their pentagonal base, such that the resulting polyhedron has 10 triangles as its faces. The pentagonal bipyramid is said to be right if the pyramids are symmetrically regular and both of their apices are on the line passing through the base's center; otherwise, it is oblique. If the pyramids are regular, then all edges of the triangular bipyramid are equal in length, making up the faces [[equilateral triangle]]s. A polyhedron with only equilateral triangles as faces is called a [[deltahedron]]. There are only eight different convex deltahedra, one of which is the pentagonal bipyramid with regular faces. More generally, the convex polyhedron in which all faces are regular is the [[Johnson solid]], and every convex deltahedra is a Johnson solid. The pentagonal bipyramid with the regular faces is among numbered the Johnson solids as <math> J_{13} </math>, the thirteenth Johnson solid.
+Like other bipyramids, the pentagonal bipyramid can be constructed by attaching the base of two pentagonal pyramids. These pyramids cover their pentagonal base, such that the resulting polyhedron has 10 triangles as its faces.{{r|trigg}} The pentagonal bipyramid is said to be right if the pyramids are symmetrically regular and both of their apices are on the line passing through the base's center; otherwise, it is oblique. If the pyramids are regular, then all edges of the triangular bipyramid are equal in length, making up the faces [[equilateral triangle]]s. A polyhedron with only equilateral triangles as faces is called a [[deltahedron]]. There are only eight different convex deltahedra, one of which is the pentagonal bipyramid with regular faces. More generally, the convex polyhedron in which all faces are regular is the [[Johnson solid]], and every convex deltahedra is a Johnson solid. The pentagonal bipyramid with the regular faces is among numbered the Johnson solids as <math> J_{13} </math>, the thirteenth Johnson solid.{{r|uehara}}
 == Properties==
@@ Line 72: / Line 72: @@
 ==References==
-{{reflist}}
+{{reflist|refs=
+<ref name="trigg">{{cite journal
+ | last = Trigg | first = Charles W.
+ | year = 1978
+ | title = An infinite class of deltahedra
+ | journal = Mathematics Magazine
+ | volume = 51
+ | issue = 1
+ | pages = 55–57
+ | doi = 10.1080/0025570X.1978.11976675
+ | jstor = 2689647
+ | mr = 1572246
+}}</ref>
+<ref name="uehara">{{cite book
+ | last = Uehara | first = Ryuhei
+ | year = 2020
+ | title = Introduction to Computational Origami: The World of New Computational Geometry
+ | url = https://books.google.com/books?id=51juDwAAQBAJ
+ | publisher = Springer
+ | isbn = 978-981-15-4470-5
+ | doi = 10.1007/978-981-15-4470-5
+ | s2cid = 220150682
+ }}</ref>
+}}
 ==External links==

Bipyramid name	Digonal bipyramid	Triangular bipyramid	Square bipyramid	Pentagonal bipyramid	Hexagonal bipyramid	...	Apeirogonal bipyramid
Polyhedron image						...
Spherical tiling image						Plane tiling image
Face config.	V2.4.4	V3.4.4	V4.4.4	V5.4.4	V6.4.4	...	V∞.4.4
Coxeter diagram						...

v t e Johnson solids
Pyramids, cupolae and rotundae	square pyramid pentagonal pyramid triangular cupola square cupola pentagonal cupola pentagonal rotunda
Modified pyramids	elongated triangular pyramid elongated square pyramid elongated pentagonal pyramid gyroelongated square pyramid gyroelongated pentagonal pyramid triangular bipyramid pentagonal bipyramid elongated triangular bipyramid elongated square bipyramid elongated pentagonal bipyramid gyroelongated square bipyramid
Modified cupolae and rotundae	elongated triangular cupola elongated square cupola elongated pentagonal cupola elongated pentagonal rotunda gyroelongated triangular cupola gyroelongated square cupola gyroelongated pentagonal cupola gyroelongated pentagonal rotunda gyrobifastigium triangular orthobicupola square orthobicupola square gyrobicupola pentagonal orthobicupola pentagonal gyrobicupola pentagonal orthocupolarotunda pentagonal gyrocupolarotunda pentagonal orthobirotunda elongated triangular orthobicupola elongated triangular gyrobicupola elongated square gyrobicupola elongated pentagonal orthobicupola elongated pentagonal gyrobicupola elongated pentagonal orthocupolarotunda elongated pentagonal gyrocupolarotunda elongated pentagonal orthobirotunda elongated pentagonal gyrobirotunda gyroelongated triangular bicupola gyroelongated square bicupola gyroelongated pentagonal bicupola gyroelongated pentagonal cupolarotunda gyroelongated pentagonal birotunda
Augmented prisms	augmented triangular prism biaugmented triangular prism triaugmented triangular prism augmented pentagonal prism biaugmented pentagonal prism augmented hexagonal prism parabiaugmented hexagonal prism metabiaugmented hexagonal prism triaugmented hexagonal prism
Modified Platonic solids	augmented dodecahedron parabiaugmented dodecahedron metabiaugmented dodecahedron triaugmented dodecahedron metabidiminished icosahedron tridiminished icosahedron augmented tridiminished icosahedron
Modified Archimedean solids	augmented truncated tetrahedron augmented truncated cube biaugmented truncated cube augmented truncated dodecahedron parabiaugmented truncated dodecahedron metabiaugmented truncated dodecahedron triaugmented truncated dodecahedron gyrate rhombicosidodecahedron parabigyrate rhombicosidodecahedron metabigyrate rhombicosidodecahedron trigyrate rhombicosidodecahedron diminished rhombicosidodecahedron paragyrate diminished rhombicosidodecahedron metagyrate diminished rhombicosidodecahedron bigyrate diminished rhombicosidodecahedron parabidiminished rhombicosidodecahedron metabidiminished rhombicosidodecahedron gyrate bidiminished rhombicosidodecahedron tridiminished rhombicosidodecahedron
Elementary solids	snub disphenoid snub square antiprism sphenocorona augmented sphenocorona sphenomegacorona hebesphenomegacorona disphenocingulum bilunabirotunda triangular hebesphenorotunda
(See also List of Johnson solids, a sortable table)