Computational physics

This article is about computational science applied in physics. For theories comparing the universe to a computer, see digital physics. For the study of the fundamental physical limits of computers, see physics of computation.

Computational physics is the study and implementation of numerical algorithms to solve problems in physics for which a quantitative theory already exists. Historically, computational physics was the first application of modern computers in science, and is now a subset of computational science.

Overview

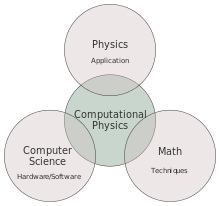
In physics, different theories based on mathematical models provide very precise predictions on how systems behave. Unfortunately, it is often the case that solving the mathematical model for a particular system in order to produce a useful prediction is not feasible. This can occur, for instance, when the solution does not have a closed-form expression, or is too complicated. In such cases, numerical approximations are required. Computational physics is the subject that deals with these numerical approximations: the approximation of the solution is written as a finite (and typically large) number of simple mathematical operations (algorithm), and a computer is used to perform these operations and compute an approximated solution and respective error.

Challenges in computational physics

Physics problems are in general very difficult to solve exactly. This is due to several (mathematical) reasons: lack of algebraic and/or analytic solubility, complexity and chaos. For example - even apparently simple problems, such as calculating the wavefunction of an electron orbiting an atom in a strong electric field, may require great effort to formulate a practical algorithm (if one can be found); other cruder or brute-force techniques, such as graphical methods or root finding, may be required. On the more advanced side, mathematical perturbation theory is also sometimes used.

In addition, the computational cost of solving quantum mechanical problems is generally of exponential in the size of the system (see computational complexity theory).^{[citation needed]} A macroscopic system typically has a size of the order of $10^{23}$ constituent particles, so it may be somewhat of an understatement to say this is a bit of a problem.

Finally, many physical systems are inherently nonlinear at best, and at worst chaotic: this means it can be difficult to ensure any numerical errors do not grow to the point of rendering the 'solution' useless.

Methods and Algorithms

Because computational physics is used in a broad class of problems, it is generally divided amongst the different mathematical problems it numerically solves, or the methods it applies. Between them, one can consider:

• ordinary differential equations (using e.g. Runge–Kutta methods)
• integration (using numerical integration or Monte Carlo integration)
• partial differential equations, for example the finite difference method, the finite element method or pseudo-spectral method
• the matrix eigenvalue problem - finding eigenvalues and their corresponding eigenvectors of very large matrices, (which correspond to eigenenergies and eigenstates in quantum physics)
• simulating physical systems (using e.g. molecular dynamics)
• protein structure prediction

Applications

Due to the broad class of problems computational physics deals, it is an essential component of modern research in different areas of physics, namely: accelerator physics, astrophysics, fluid mechanics (computational fluid dynamics), lattice field theory/lattice gauge theory (especially lattice quantum chromodynamics), plasma physics (see plasma modeling), solid state physics, soft condensed matter physics, etc.

See also

• Important publications in computational physics
• Computational magnetohydrodynamics
• Division of Computational Physics (DCOMP) of the American Physical Society
• CECAM - Centre européen de calcul atomique et moléculaire
• Mathematical physics
• Open Source Physics, computational physics libraries and pedagogical tools

Further reading

• A.K. Hartmann, Practical Guide to Computer Simulations, World Scientific (2009)
• International Journal of Modern Physics C (IJMPC): Physics and Computers, World Scientific
• Steven E. Koonin, Computational Physics, Addison-Wesley (1986)
• R.H. Landau, C.C. Bordeianu, and M. Jose Paez, A Survey of Computational Physics: Introductory Computational Science, Princeton University Press (2008)
• T. Pang, An Introduction to Computational Physics, Cambridge University Press (2010)
• J. Thijssen, Computational Physics, Cambridge University Press (2007)

External links

• C20 IUPAP Commission on Computational Physics
• APS DCOMP
• IoP CPG (UK)
• SciDAC: Scientific Discovery through Advanced Computing
• Open Source Physics
• SCINET Scientific Software Framework