Multiplication algorithm
The article's lead section may need to be rewritten. (August 2022) |
A multiplication algorithm is an algorithm (or method) to multiply two numbers. Depending on the size of the numbers, different algorithms are more efficient than others. Efficient multiplication algorithms have existed since the advent of the decimal numeral system.
Long multiplication[edit]
If a positional numeral system is used, a natural way of multiplying numbers is taught in schools as long multiplication, sometimes called grade-school multiplication, sometimes called the Standard Algorithm: multiply the multiplicand by each digit of the multiplier and then add up all the properly shifted results. It requires memorization of the multiplication table for single digits.
This is the usual algorithm for multiplying larger numbers by hand in base 10. A person doing long multiplication on paper will write down all the products and then add them together; an abacus-user will sum the products as soon as each one is computed.
Example[edit]
This example uses long multiplication to multiply 23,958,233 (multiplicand) by 5,830 (multiplier) and arrives at 139,676,498,390 for the result (product).
23958233
× 5830
———————————————
00000000 ( = 23,958,233 × 0)
71874699 ( = 23,958,233 × 30)
191665864 ( = 23,958,233 × 800)
+ 119791165 ( = 23,958,233 × 5,000)
———————————————
139676498390 ( = 139,676,498,390)
Other notations[edit]
In some countries such as Germany, the above multiplication is depicted similarly but with the original product kept horizontal and computation starting with the first digit of the multiplier:[1]
23958233 · 5830
———————————————
119791165
191665864
71874699
00000000
———————————————
139676498390
Below pseudocode describes the process of above multiplication. It keeps only one row to maintain the sum which finally becomes the result. Note that the '+=' operator is used to denote sum to existing value and store operation (akin to languages such as Java and C) for compactness.
multiply(a[1..p], b[1..q], base) // Operands containing rightmost digits at index 1
product = [1..p+q] // Allocate space for result
for b_i = 1 to q // for all digits in b
carry = 0
for a_i = 1 to p // for all digits in a
product[a_i + b_i - 1] += carry + a[a_i] * b[b_i]
carry = product[a_i + b_i - 1] / base
product[a_i + b_i - 1] = product[a_i + b_i - 1] mod base
product[b_i + p] = carry // last digit comes from final carry
return product
Usage in computers[edit]
Some chips implement long multiplication, in hardware or in microcode, for various integer and floating-point word sizes. In arbitrary-precision arithmetic, it is common to use long multiplication with the base set to 2w, where w is the number of bits in a word, for multiplying relatively small numbers. To multiply two numbers with n digits using this method, one needs about n2 operations. More formally, multiplying two n-digit numbers using long multiplication requires Θ(n2) single-digit operations (additions and multiplications).
When implemented in software, long multiplication algorithms must deal with overflow during additions, which can be expensive. A typical solution is to represent the number in a small base, b, such that, for example, 8b is a representable machine integer. Several additions can then be performed before an overflow occurs. When the number becomes too large, we add part of it to the result, or we carry and map the remaining part back to a number that is less than b. This process is called normalization. Richard Brent used this approach in his Fortran package, MP.[2]
Computers initially used a very similar algorithm to long multiplication in base 2, but modern processors have optimized circuitry for fast multiplications using more efficient algorithms, at the price of a more complex hardware realization.[citation needed] In base two, long multiplication is sometimes called "shift and add", because the algorithm simplifies and just consists of shifting left (multiplying by powers of two) and adding. Most currently available microprocessors implement this or other similar algorithms (such as Booth encoding) for various integer and floating-point sizes in hardware multipliers or in microcode.[citation needed]
On currently available processors, a bit-wise shift instruction is usually (but not always) faster than a multiply instruction and can be used to multiply (shift left) and divide (shift right) by powers of two. Multiplication by a constant and division by a constant can be implemented using a sequence of shifts and adds or subtracts. For example, there are several ways to multiply by 10 using only bit-shift and addition.
((x << 2) + x) << 1 # Here 10*x is computed as (x*2^2 + x)*2
(x << 3) + (x << 1) # Here 10*x is computed as x*2^3 + x*2
In some cases such sequences of shifts and adds or subtracts will outperform hardware multipliers and especially dividers. A division by a number of the form or often can be converted to such a short sequence.
Algorithms for multiplying by hand[edit]
In addition to the standard long multiplication, there are several other methods used to perform multiplication by hand. Such algorithms may be devised for speed, ease of calculation, or educational value, particularly when computers or multiplication tables are unavailable.
Grid method[edit]
The grid method (or box method) is an introductory method for multiple-digit multiplication that is often taught to pupils at primary school or elementary school. It has been a standard part of the national primary school mathematics curriculum in England and Wales since the late 1990s.[3]
Both factors are broken up ("partitioned") into their hundreds, tens and units parts, and the products of the parts are then calculated explicitly in a relatively simple multiplication-only stage, before these contributions are then totalled to give the final answer in a separate addition stage.
The calculation 34 × 13, for example, could be computed using the grid:
300 40 90 + 12 ———— 442
| × | 30 | 4 |
|---|---|---|
| 10 | 300 | 40 |
| 3 | 90 | 12 |
followed by addition to obtain 442, either in a single sum (see right), or through forming the row-by-row totals (300 + 40) + (90 + 12) = 340 + 102 = 442.
This calculation approach (though not necessarily with the explicit grid arrangement) is also known as the partial products algorithm. Its essence is the calculation of the simple multiplications separately, with all addition being left to the final gathering-up stage.
The grid method can in principle be applied to factors of any size, although the number of sub-products becomes cumbersome as the number of digits increases. Nevertheless, it is seen as a usefully explicit method to introduce the idea of multiple-digit multiplications; and, in an age when most multiplication calculations are done using a calculator or a spreadsheet, it may in practice be the only multiplication algorithm that some students will ever need.
Lattice multiplication[edit]
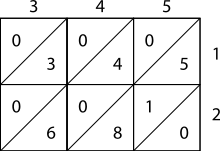

Lattice, or sieve, multiplication is algorithmically equivalent to long multiplication. It requires the preparation of a lattice (a grid drawn on paper) which guides the calculation and separates all the multiplications from the additions. It was introduced to Europe in 1202 in Fibonacci's Liber Abaci. Fibonacci described the operation as mental, using his right and left hands to carry the intermediate calculations. Matrakçı Nasuh presented 6 different variants of this method in this 16th-century book, Umdet-ul Hisab. It was widely used in Enderun schools across the Ottoman Empire.[4] Napier's bones, or Napier's rods also used this method, as published by Napier in 1617, the year of his death.
As shown in the example, the multiplicand and multiplier are written above and to the right of a lattice, or a sieve. It is found in Muhammad ibn Musa al-Khwarizmi's "Arithmetic", one of Leonardo's sources mentioned by Sigler, author of "Fibonacci's Liber Abaci", 2002.[citation needed]
- During the multiplication phase, the lattice is filled in with two-digit products of the corresponding digits labeling each row and column: the tens digit goes in the top-left corner.
- During the addition phase, the lattice is summed on the diagonals.
- Finally, if a carry phase is necessary, the answer as shown along the left and bottom sides of the lattice is converted to normal form by carrying ten's digits as in long addition or multiplication.
Example[edit]
The pictures on the right show how to calculate 345 × 12 using lattice multiplication. As a more complicated example, consider the picture below displaying the computation of 23,958,233 multiplied by 5,830 (multiplier); the result is 139,676,498,390. Notice 23,958,233 is along the top of the lattice and 5,830 is along the right side. The products fill the lattice and the sum of those products (on the diagonal) are along the left and bottom sides. Then those sums are totaled as shown.
2 3 9 5 8 2 3 3
+---+---+---+---+---+---+---+---+-
|1 /|1 /|4 /|2 /|4 /|1 /|1 /|1 /|
| / | / | / | / | / | / | / | / | 5
01|/ 0|/ 5|/ 5|/ 5|/ 0|/ 0|/ 5|/ 5|
+---+---+---+---+---+---+---+---+-
|1 /|2 /|7 /|4 /|6 /|1 /|2 /|2 /|
| / | / | / | / | / | / | / | / | 8
02|/ 6|/ 4|/ 2|/ 0|/ 4|/ 6|/ 4|/ 4|
+---+---+---+---+---+---+---+---+-
|0 /|0 /|2 /|1 /|2 /|0 /|0 /|0 /|
| / | / | / | / | / | / | / | / | 3
17|/ 6|/ 9|/ 7|/ 5|/ 4|/ 6|/ 9|/ 9|
+---+---+---+---+---+---+---+---+-
|0 /|0 /|0 /|0 /|0 /|0 /|0 /|0 /|
| / | / | / | / | / | / | / | / | 0
24|/ 0|/ 0|/ 0|/ 0|/ 0|/ 0|/ 0|/ 0|
+---+---+---+---+---+---+---+---+-
26 15 13 18 17 13 09 00
|
01 002 0017 00024 000026 0000015 00000013 000000018 0000000017 00000000013 000000000009 0000000000000 ————————————— 139676498390 |
= 139,676,498,390 |
Russian peasant multiplication[edit]
The binary method is also known as peasant multiplication, because it has been widely used by people who are classified as peasants and thus have not memorized the multiplication tables required for long multiplication.[5][failed verification] The algorithm was in use in ancient Egypt.[6] Its main advantages are that it can be taught quickly, requires no memorization, and can be performed using tokens, such as poker chips, if paper and pencil aren't available. The disadvantage is that it takes more steps than long multiplication, so it can be unwieldy for large numbers.
Description[edit]
On paper, write down in one column the numbers you get when you repeatedly halve the multiplier, ignoring the remainder; in a column beside it repeatedly double the multiplicand. Cross out each row in which the last digit of the first number is even, and add the remaining numbers in the second column to obtain the product.
Examples[edit]
This example uses peasant multiplication to multiply 11 by 3 to arrive at a result of 33.
Decimal: Binary: 11 3 1011 11 5 6 101 110 2121011001 24 1 11000 —— —————— 33 100001
Describing the steps explicitly:
- 11 and 3 are written at the top
- 11 is halved (5.5) and 3 is doubled (6). The fractional portion is discarded (5.5 becomes 5).
- 5 is halved (2.5) and 6 is doubled (12). The fractional portion is discarded (2.5 becomes 2). The figure in the left column (2) is even, so the figure in the right column (12) is discarded.
- 2 is halved (1) and 12 is doubled (24).
- All not-scratched-out values are summed: 3 + 6 + 24 = 33.
The method works because multiplication is distributive, so:
A more complicated example, using the figures from the earlier examples (23,958,233 and 5,830):
Decimal: Binary: 583023958233101101100011010110110110010010110110012915 47916466 101101100011 10110110110010010110110010 1457 95832932 10110110001 101101101100100101101100100 72819166586410110110001011011011001001011011001000364383331728101101100101101101100100101101100100001827666634561011011010110110110010010110110010000091 1533326912 1011011 1011011011001001011011001000000 45 3066653824 101101 10110110110010010110110010000000 2261333076481011010110110110010010110110010000000011 12266615296 1011 1011011011001001011011001000000000 5 24533230592 101 10110110110010010110110010000000000 249066461184101011011011001001011011001000000000001 98132922368 1 1011011011001001011011001000000000000 ———————————— 1022143253354344244353353243222210110 (before carry) 139676498390 10000010000101010111100011100111010110
Quarter square multiplication[edit]
This formula can in some cases be used, to make multiplication tasks easier to complete:
In the case where and are integers, we have that
because and are either both even or both odd. This means that
and it's sufficient to (pre-)compute the integral part of squares divided by 4 like in the following example.
Examples[edit]
Below is a lookup table of quarter squares with the remainder discarded for the digits 0 through 18; this allows for the multiplication of numbers up to 9×9.
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| ⌊n2/4⌋ | 0 | 0 | 1 | 2 | 4 | 6 | 9 | 12 | 16 | 20 | 25 | 30 | 36 | 42 | 49 | 56 | 64 | 72 | 81 |
If, for example, you wanted to multiply 9 by 3, you observe that the sum and difference are 12 and 6 respectively. Looking both those values up on the table yields 36 and 9, the difference of which is 27, which is the product of 9 and 3.
History of quarter square multiplication[edit]
In prehistoric time, quarter square multiplication involved floor function; that some sources[7][8] attribute to Babylonian mathematics (2000–1600 BC).
Antoine Voisin published a table of quarter squares from 1 to 1000 in 1817 as an aid in multiplication. A larger table of quarter squares from 1 to 100000 was published by Samuel Laundy in 1856,[9] and a table from 1 to 200000 by Joseph Blater in 1888.[10]
Quarter square multipliers were used in analog computers to form an analog signal that was the product of two analog input signals. In this application, the sum and difference of two input voltages are formed using operational amplifiers. The square of each of these is approximated using piecewise linear circuits. Finally the difference of the two squares is formed and scaled by a factor of one fourth using yet another operational amplifier.
In 1980, Everett L. Johnson proposed using the quarter square method in a digital multiplier.[11] To form the product of two 8-bit integers, for example, the digital device forms the sum and difference, looks both quantities up in a table of squares, takes the difference of the results, and divides by four by shifting two bits to the right. For 8-bit integers the table of quarter squares will have 29−1=511 entries (one entry for the full range 0..510 of possible sums, the differences using only the first 256 entries in range 0..255) or 29−1=511 entries (using for negative differences the technique of 2-complements and 9-bit masking, which avoids testing the sign of differences), each entry being 16-bit wide (the entry values are from (0²/4)=0 to (510²/4)=65025).
The quarter square multiplier technique has benefited 8-bit systems that do not have any support for a hardware multiplier. Charles Putney implemented this for the 6502.[12]
Computational complexity of multiplication[edit]
What is the fastest algorithm for multiplication of two -digit numbers?
A line of research in theoretical computer science is about the number of single-bit arithmetic operations necessary to multiply two -bit integers. This is known as the computational complexity of multiplication. Usual algorithms done by hand have asymptotic complexity of , but in 1960 Anatoly Karatsuba discovered that better complexity was possible (with the Karatsuba algorithm).
Currently, the algorithm with the best computational complexity is a 2019 algorithm of David Harvey and Joris van der Hoeven, which uses the strategies of using number-theoretic transforms introduced with the Schönhage–Strassen algorithm to multiply integers using only operations.[13] This is conjectured to be the best possible algorithm, but lower bounds of are not known.
Karatsuba multiplication[edit]
Karatsuba multiplication is an O(nlog23) ≈ O(n1.585) divide and conquer algorithm, that uses recursion to merge together sub calculations.
By rewriting the formula, one makes it possible to do sub calculations / recursion. By doing recursion, one can solve this in a fast manner.
Let and be represented as -digit strings in some base . For any positive integer less than , one can write the two given numbers as
where and are less than . The product is then
where
These formulae require four multiplications and were known to Charles Babbage.[14] Karatsuba observed that can be computed in only three multiplications, at the cost of a few extra additions. With and as before one can observe that
Because of the overhead of recursion, Karatsuba's multiplication is slower than long multiplication for small values of n; typical implementations therefore switch to long multiplication for small values of n.
General case with multiplication of N numbers[edit]
By exploring patterns after expansion, one see following:
Each summand is associated to a unique binary number from 0 to , for example etc. Furthermore; B is powered to number of 1, in this binary string, multiplied with m.
If we express this in fewer terms, we get:
, where means digit in number i at position j. Notice that
History[edit]
Karatsuba's algorithm was the first known algorithm for multiplication that is asymptotically faster than long multiplication,[15] and can thus be viewed as the starting point for the theory of fast multiplications.
Toom–Cook[edit]
Another method of multiplication is called Toom–Cook or Toom-3. The Toom–Cook method splits each number to be multiplied into multiple parts. The Toom–Cook method is one of the generalizations of the Karatsuba method. A three-way Toom–Cook can do a size-3N multiplication for the cost of five size-N multiplications. This accelerates the operation by a factor of 9/5, while the Karatsuba method accelerates it by 4/3.
Although using more and more parts can reduce the time spent on recursive multiplications further, the overhead from additions and digit management also grows. For this reason, the method of Fourier transforms is typically faster for numbers with several thousand digits, and asymptotically faster for even larger numbers.
Schönhage–Strassen[edit]

Every number in base B, can be written as a polynomial:
Furthermore, multiplication of two numbers could be thought of as a product of two polynomials:
Because,for : , we have a convolution.
By using fft (fast fourier transformation) with convolution rule, we can get
● . That is; ● , where is the corresponding coefficient in fourier space. This can also be written as: fft(a * b) = fft(a) ● fft(b).
We have the same coefficient due to linearity under fourier transformation, and because these polynomials
only consist of one unique term per coefficient:
and
Convolution rule: ●
We have reduced our convolution problem
to product problem, through fft.
By finding ifft (polynomial interpolation), for each , one get the desired coefficients.
Algorithm uses divide and conquer strategy, to divide problem to subproblems.
It has a time complexity of O(n log(n) log(log(n))).
History[edit]
Algorithm were invented by Strassen (1968). The algorithm was made practical and theoretical guarantees were provided in 1971 by Schönhage and Strassen resulting in the Schönhage–Strassen algorithm.[16]
Further improvements[edit]
In 2007 the asymptotic complexity of integer multiplication was improved by the Swiss mathematician Martin Fürer of Pennsylvania State University to n log(n) 2Θ(log*(n)) using Fourier transforms over complex numbers,[17] where log* denotes the iterated logarithm. Anindya De, Chandan Saha, Piyush Kurur and Ramprasad Saptharishi gave a similar algorithm using modular arithmetic in 2008 achieving the same running time.[18] In context of the above material, what these latter authors have achieved is to find N much less than 23k + 1, so that Z/NZ has a (2m)th root of unity. This speeds up computation and reduces the time complexity. However, these latter algorithms are only faster than Schönhage–Strassen for impractically large inputs.
In 2014, Harvey, Joris van der Hoeven and Lecerf[19] gave a new algorithm that achieves a running time of , making explicit the implied constant in the exponent. They also proposed a variant of their algorithm which achieves but whose validity relies on standard conjectures about the distribution of Mersenne primes. In 2016, Covanov and Thomé proposed an integer multiplication algorithm based on a generalization of Fermat primes that conjecturally achieves a complexity bound of . This matches the 2015 conditional result of Harvey, van der Hoeven, and Lecerf but uses a different algorithm and relies on a different conjecture.[20] In 2018, Harvey and van der Hoeven used an approach based on the existence of short lattice vectors guaranteed by Minkowski's theorem to prove an unconditional complexity bound of .[21]
In March 2019, David Harvey and Joris van der Hoeven announced their discovery of an O(n log n) multiplication algorithm.[22] It was published in the Annals of Mathematics in 2021.[23] Because Schönhage and Strassen predicted that n log(n) is the "best possible" result, Harvey said: "... our work is expected to be the end of the road for this problem, although we don't know yet how to prove this rigorously."[24]
Lower bounds[edit]
There is a trivial lower bound of Ω(n) for multiplying two n-bit numbers on a single processor; no matching algorithm (on conventional machines, that is on Turing equivalent machines) nor any sharper lower bound is known. Multiplication lies outside of AC0[p] for any prime p, meaning there is no family of constant-depth, polynomial (or even subexponential) size circuits using AND, OR, NOT, and MODp gates that can compute a product. This follows from a constant-depth reduction of MODq to multiplication.[25] Lower bounds for multiplication are also known for some classes of branching programs.[26]
Complex number multiplication[edit]
Complex multiplication normally involves four multiplications and two additions.
Or
As observed by Peter Ungar in 1963, one can reduce the number of multiplications to three, using essentially the same computation as Karatsuba's algorithm.[27] The product (a + bi) · (c + di) can be calculated in the following way.
- k1 = c · (a + b)
- k2 = a · (d − c)
- k3 = b · (c + d)
- Real part = k1 − k3
- Imaginary part = k1 + k2.
This algorithm uses only three multiplications, rather than four, and five additions or subtractions rather than two. If a multiply is more expensive than three adds or subtracts, as when calculating by hand, then there is a gain in speed. On modern computers a multiply and an add can take about the same time so there may be no speed gain. There is a trade-off in that there may be some loss of precision when using floating point.
For fast Fourier transforms (FFTs) (or any linear transformation) the complex multiplies are by constant coefficients c + di (called twiddle factors in FFTs), in which case two of the additions (d−c and c+d) can be precomputed. Hence, only three multiplies and three adds are required.[28] However, trading off a multiplication for an addition in this way may no longer be beneficial with modern floating-point units.[29]
Polynomial multiplication[edit]
All the above multiplication algorithms can also be expanded to multiply polynomials. Alternatively the Kronecker substitution technique may be used to convert the problem of multiplying polynomials into a single binary multiplication.[30]
Long multiplication methods can be generalised to allow the multiplication of algebraic formulae:
14ac - 3ab + 2 multiplied by ac - ab + 1
14ac -3ab 2
ac -ab 1
————————————————————
14a2c2 -3a2bc 2ac
-14a2bc 3 a2b2 -2ab
14ac -3ab 2
———————————————————————————————————————
14a2c2 -17a2bc 16ac 3a2b2 -5ab +2
=======================================[31]
As a further example of column based multiplication, consider multiplying 23 long tons (t), 12 hundredweight (cwt) and 2 quarters (qtr) by 47. This example uses avoirdupois measures: 1 t = 20 cwt, 1 cwt = 4 qtr.
t cwt qtr
23 12 2
47 x
————————————————
141 94 94
940 470
29 23
————————————————
1110 587 94
————————————————
1110 7 2
================= Answer: 1110 ton 7 cwt 2 qtr
First multiply the quarters by 47, the result 94 is written into the first workspace. Next, multiply cwt 12*47 = (2 + 10)*47 but don't add up the partial results (94, 470) yet. Likewise multiply 23 by 47 yielding (141, 940). The quarters column is totaled and the result placed in the second workspace (a trivial move in this case). 94 quarters is 23 cwt and 2 qtr, so place the 2 in the answer and put the 23 in the next column left. Now add up the three entries in the cwt column giving 587. This is 29 t 7 cwt, so write the 7 into the answer and the 29 in the column to the left. Now add up the tons column. There is no adjustment to make, so the result is just copied down.
The same layout and methods can be used for any traditional measurements and non-decimal currencies such as the old British £sd system.
See also[edit]
- Binary multiplier
- Dadda multiplier
- Division algorithm
- Horner scheme for evaluating of a polynomial
- Logarithm
- Mental calculation
- Number-theoretic transform
- Prosthaphaeresis
- Slide rule
- Trachtenberg system
- Residue number system § Multiplication for another fast multiplication algorithm, specially efficient when many operations are done in sequence, such as in linear algebra
- Wallace tree
References[edit]
- ^ "Multiplication". www.mathematische-basteleien.de. Retrieved 2022-03-15.
- ^ Brent, Richard P (March 1978). "A Fortran Multiple-Precision Arithmetic Package". ACM Transactions on Mathematical Software. 4: 57–70. CiteSeerX 10.1.1.117.8425. doi:10.1145/355769.355775. S2CID 8875817.
- ^ Eason, Gary (2000-02-13). "Back to school for parents". BBC News.
Eastaway, Rob (2010-09-10). "Why parents can't do maths today". BBC News. - ^ Corlu, M.S.; Burlbaw, L.M.; Capraro, R.M.; Corlu, M.A.; Han, S. (2010). "The Ottoman Palace School Enderun and the Man with Multiple Talents, Matrakçı Nasuh". Journal of the Korea Society of Mathematical Education Series D: Research in Mathematical Education. 14 (1): 19–31.
- ^ Bogomolny, Alexander. "Peasant Multiplication". www.cut-the-knot.org. Retrieved 2017-11-04.
- ^ Wells, D. (1987). The Penguin Dictionary of Curious and Interesting Numbers. Penguin Books. p. 44. ISBN 978-0-14-008029-2.
- ^ McFarland, David (2007), Quarter Tables Revisited: Earlier Tables, Division of Labor in Table Construction, and Later Implementations in Analog Computers, p. 1
- ^ Robson, Eleanor (2008). Mathematics in Ancient Iraq: A Social History. Princeton University Press. p. 227. ISBN 978-0691201405.
- ^ "Reviews", The Civil Engineer and Architect's Journal: 54–55, 1857.
- ^ Holmes, Neville (2003), "Multiplying with quarter squares", The Mathematical Gazette, 87 (509): 296–299, doi:10.1017/S0025557200172778, JSTOR 3621048, S2CID 125040256.
- ^ Everett L., Johnson (March 1980), "A Digital Quarter Square Multiplier", IEEE Transactions on Computers, vol. C-29, no. 3, Washington, DC, USA: IEEE Computer Society, pp. 258–261, doi:10.1109/TC.1980.1675558, ISSN 0018-9340, S2CID 24813486
- ^ Putney, Charles (March 1986). "Fastest 6502 Multiplication Yet". Apple Assembly Line. 6 (6).
- ^ Harvey, David; van der Hoeven, Joris (2021). "Integer multiplication in time " (PDF). Annals of Mathematics. Second Series. 193 (2): 563–617. doi:10.4007/annals.2021.193.2.4. MR 4224716. S2CID 109934776.
- ^ Charles Babbage, Chapter VIII – Of the Analytical Engine, Larger Numbers Treated, Passages from the Life of a Philosopher, Longman Green, London, 1864; page 125.
- ^ D. Knuth, The Art of Computer Programming, vol. 2, sec. 4.3.3 (1998)
- ^ Schönhage, A.; Strassen, V. (1971). "Schnelle Multiplikation großer Zahlen". Computing. 7 (3–4): 281–292. doi:10.1007/BF02242355. S2CID 9738629.
- ^ Fürer, M. (2007). "Faster Integer Multiplication" (PDF). Proceedings of the thirty-ninth annual ACM symposium on Theory of computing, June 11–13, 2007, San Diego, California, USA. pp. 57–66. doi:10.1145/1250790.1250800. ISBN 978-1-59593-631-8. S2CID 8437794.
- ^ De, A.; Saha, C.; Kurur, P.; Saptharishi, R. (2008). "Fast integer multiplication using modular arithmetic". Proceedings of the 40th annual ACM Symposium on Theory of Computing (STOC). pp. 499–506. arXiv:0801.1416. doi:10.1145/1374376.1374447. ISBN 978-1-60558-047-0. S2CID 3264828.
- ^ Harvey, David; van der Hoeven, Joris; Lecerf, Grégoire (2016). "Even faster integer multiplication". Journal of Complexity. 36: 1–30. arXiv:1407.3360. doi:10.1016/j.jco.2016.03.001. MR 3530637.
- ^ Covanov, Svyatoslav; Thomé, Emmanuel (2019). "Fast Integer Multiplication Using Generalized Fermat Primes". Math. Comp. 88 (317): 1449–1477. arXiv:1502.02800. doi:10.1090/mcom/3367. S2CID 67790860.
- ^ Harvey, D.; van der Hoeven, J. (2019). "Faster integer multiplication using short lattice vectors". The Open Book Series. 2: 293–310. arXiv:1802.07932. doi:10.2140/obs.2019.2.293. S2CID 3464567.
- ^ Hartnett, Kevin (2019-04-11). "Mathematicians Discover the Perfect Way to Multiply". Quanta Magazine. Retrieved 2019-05-03.
- ^ Harvey, David; van der Hoeven, Joris (2021). "Integer multiplication in time " (PDF). Annals of Mathematics. Second Series. 193 (2): 563–617. doi:10.4007/annals.2021.193.2.4. MR 4224716. S2CID 109934776.
- ^ Gilbert, Lachlan (2019-04-04). "Maths whiz solves 48-year-old multiplication problem". UNSW. Retrieved 2019-04-18.
- ^ Arora, Sanjeev; Barak, Boaz (2009). Computational Complexity: A Modern Approach. Cambridge University Press. ISBN 978-0-521-42426-4.
- ^ Ablayev, F.; Karpinski, M. (2003). "A lower bound for integer multiplication on randomized ordered read-once branching programs" (PDF). Information and Computation. 186 (1): 78–89. doi:10.1016/S0890-5401(03)00118-4.
- ^ Knuth, Donald E. (1988), The Art of Computer Programming volume 2: Seminumerical algorithms, Addison-Wesley, pp. 519, 706
- ^ Duhamel, P.; Vetterli, M. (1990). "Fast Fourier transforms: A tutorial review and a state of the art" (PDF). Signal Processing. 19 (4): 259–299 See Section 4.1. doi:10.1016/0165-1684(90)90158-U.
- ^ Johnson, S.G.; Frigo, M. (2007). "A modified split-radix FFT with fewer arithmetic operations" (PDF). IEEE Trans. Signal Process. 55 (1): 111–9 See Section IV. Bibcode:2007ITSP...55..111J. doi:10.1109/TSP.2006.882087. S2CID 14772428.
- ^ von zur Gathen, Joachim; Gerhard, Jürgen (1999), Modern Computer Algebra, Cambridge University Press, pp. 243–244, ISBN 978-0-521-64176-0.
- ^ Castle, Frank (1900). Workshop Mathematics. London: MacMillan and Co. p. 74.
Further reading[edit]
- Warren Jr., Henry S. (2013). Hacker's Delight (2 ed.). Addison Wesley - Pearson Education, Inc. ISBN 978-0-321-84268-8.
- Savard, John J. G. (2018) [2006]. "Advanced Arithmetic Techniques". quadibloc. Archived from the original on 2018-07-03. Retrieved 2018-07-16.
- Johansson, Kenny (2008). Low Power and Low Complexity Shift-and-Add Based Computations (PDF) (Dissertation thesis). Linköping Studies in Science and Technology (1 ed.). Linköping, Sweden: Department of Electrical Engineering, Linköping University. ISBN 978-91-7393-836-5. ISSN 0345-7524. No. 1201. Archived (PDF) from the original on 2017-08-13. Retrieved 2021-08-23. (x+268 pages)
External links[edit]
Basic arithmetic[edit]
- The Many Ways of Arithmetic in UCSMP Everyday Mathematics
- A Powerpoint presentation about ancient mathematics
- Lattice Multiplication Flash Video





























































