Finite subdivision rule

In mathematics, a finite subdivision rule is a recursive way of dividing a polygon or other two-dimensional shape into smaller and smaller pieces. Subdivision rules in a sense are generalizations of regular geometric fractals. Instead of repeating exactly the same design over and over, they have slight variations in each stage, allowing a richer structure while maintaining the elegant style of fractals.[1] Subdivision rules have been used in architecture, biology, and computer science, as well as in the study of hyperbolic manifolds. Substitution tilings are a well-studied type of subdivision rule.
Definition[edit]
A subdivision rule takes a tiling of the plane by polygons and turns it into a new tiling by subdividing each polygon into smaller polygons. It is finite if there are only finitely many ways that every polygon can subdivide. Each way of subdividing a tile is called a tile type. Each tile type is represented by a label (usually a letter). Every tile type subdivides into smaller tile types. Each edge also gets subdivided according to finitely many edge types. Finite subdivision rules can only subdivide tilings that are made up of polygons labelled by tile types. Such tilings are called subdivision complexes for the subdivision rule. Given any subdivision complex for a subdivision rule, we can subdivide it over and over again to get a sequence of tilings.
For instance, binary subdivision has one tile type and one edge type:

Since the only tile type is a quadrilateral, binary subdivision can only subdivide tilings made up of quadrilaterals. This means that the only subdivision complexes are tilings by quadrilaterals. The tiling can be regular, but doesn't have to be:

Here we start with a complex made of four quadrilaterals and subdivide it twice. All quadrilaterals are type A tiles.
Examples of finite subdivision rules[edit]
Barycentric subdivision is an example of a subdivision rule with one edge type (that gets subdivided into two edges) and one tile type (a triangle that gets subdivided into 6 smaller triangles). Any triangulated surface is a barycentric subdivision complex.[1]
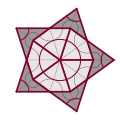
The Penrose tiling can be generated by a subdivision rule on a set of four tile types (the curved lines in the table below only help to show how the tiles fit together):
| Name | Initial tiles | Generation 1 | Generation 2 | Generation 3 |
|---|---|---|---|---|
| Half-kite | 
|

|

|

|
| Half-dart | 
|

|

|

|
| Sun | 
|

|

|

|
| Star | 
|
|

|

|
Certain rational maps give rise to finite subdivision rules.[2] This includes most Lattès maps.[3]
Every prime, non-split alternating knot or link complement has a subdivision rule, with some tiles that do not subdivide, corresponding to the boundary of the link complement.[4] The subdivision rules show what the night sky would look like to someone living in a knot complement; because the universe wraps around itself (i.e. is not simply connected), an observer would see the visible universe repeat itself in an infinite pattern. The subdivision rule describes that pattern.
The subdivision rule looks different for different geometries. This is a subdivision rule for the trefoil knot, which is not a hyperbolic knot:
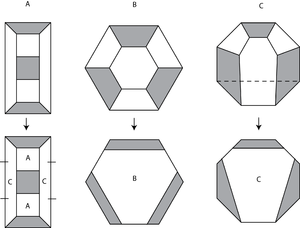
And this is the subdivision rule for the Borromean rings, which is hyperbolic:

In each case, the subdivision rule would act on some tiling of a sphere (i.e. the night sky), but it is easier to just draw a small part of the night sky, corresponding to a single tile being repeatedly subdivided. This is what happens for the trefoil knot:

And for the Borromean rings:
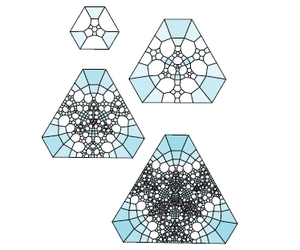
Subdivision rules in higher dimensions[edit]
Subdivision rules can easily be generalized to other dimensions.[5] For instance, barycentric subdivision is used in all dimensions. Also, binary subdivision can be generalized to other dimensions (where hypercubes get divided by every midplane), as in the proof of the Heine–Borel theorem.
Rigorous definition[edit]

A finite subdivision rule consists of the following.[1]
1. A finite 2-dimensional CW complex , called the subdivision complex, with a fixed cell structure such that is the union of its closed 2-cells. We assume that for each closed 2-cell of there is a CW structure on a closed 2-disk such that has at least two vertices, the vertices and edges of are contained in , and the characteristic map which maps onto restricts to a homeomorphism onto each open cell.
2. A finite two dimensional CW complex , which is a subdivision of .
3.A continuous cellular map called the subdivision map, whose restriction to every open cell is a homeomorphism onto an open cell.
Each CW complex in the definition above (with its given characteristic map ) is called a tile type.
An -complex for a subdivision rule is a 2-dimensional CW complex which is the union of its closed 2-cells, together with a continuous cellular map whose restriction to each open cell is a homeomorphism. We can subdivide into a complex by requiring that the induced map restricts to a homeomorphism onto each open cell. is again an -complex with map . By repeating this process, we obtain a sequence of subdivided -complexes with maps .
Binary subdivision is one example:[6]

The subdivision complex can be created by gluing together the opposite edges of the square, making the subdivision complex into a torus. The subdivision map is the doubling map on the torus, wrapping the meridian around itself twice and the longitude around itself twice. This is a four-fold covering map. The plane, tiled by squares, is a subdivision complex for this subdivision rule, with the structure map given by the standard covering map. Under subdivision, each square in the plane gets subdivided into squares of one-fourth the size.
Quasi-isometry properties[edit]

Subdivision rules can be used to study the quasi-isometry properties of certain spaces.[7] Given a subdivision rule and subdivision complex , we can construct a graph called the history graph that records the action of the subdivision rule. The graph consists of the dual graphs of every stage , together with edges connecting each tile in with its subdivisions in .
The quasi-isometry properties of the history graph can be studied using subdivision rules. For instance, the history graph is quasi-isometric to hyperbolic space exactly when the subdivision rule is conformal, as described in the combinatorial Riemann mapping theorem.[7]
Applications[edit]
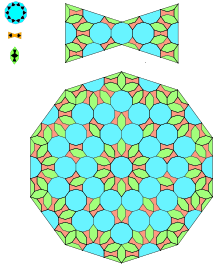
Islamic Girih tiles in Islamic architecture are self-similar tilings that can be modeled with finite subdivision rules.[8] In 2007, Peter J. Lu of Harvard University and Professor Paul J. Steinhardt of Princeton University published a paper in the journal Science suggesting that girih tilings possessed properties consistent with self-similar fractal quasicrystalline tilings such as Penrose tilings (presentation 1974, predecessor works starting in about 1964) predating them by five centuries.[8]
Subdivision surfaces in computer graphics use subdivision rules to refine a surface to any given level of precision. These subdivision surfaces (such as the Catmull-Clark subdivision surface) take a polygon mesh (the kind used in 3D animated movies) and refines it to a mesh with more polygons by adding and shifting points according to different recursive formulas.[9] Although many points get shifted in this process, each new mesh is combinatorially a subdivision of the old mesh (meaning that for every edge and vertex of the old mesh, you can identify a corresponding edge and vertex in the new one, plus several more edges and vertices).
Subdivision rules were applied by Cannon, Floyd and Parry (2000) to the study of large-scale growth patterns of biological organisms.[6] Cannon, Floyd and Parry produced a mathematical growth model which demonstrated that some systems determined by simple finite subdivision rules can results in objects (in their example, a tree trunk) whose large-scale form oscillates wildly over time even though the local subdivision laws remain the same.[6] Cannon, Floyd and Parry also applied their model to the analysis of the growth patterns of rat tissue.[6] They suggested that the "negatively curved" (or non-euclidean) nature of microscopic growth patterns of biological organisms is one of the key reasons why large-scale organisms do not look like crystals or polyhedral shapes but in fact in many cases resemble self-similar fractals.[6] In particular they suggested that such "negatively curved" local structure is manifested in highly folded and highly connected nature of the brain and the lung tissue.[6]
Cannon's conjecture[edit]
Cannon, Floyd, and Parry first studied finite subdivision rules in an attempt to prove the following conjecture:
Cannon's conjecture: Every Gromov hyperbolic group with a 2-sphere at infinity acts geometrically on hyperbolic 3-space.[7]
Here, a geometric action is a cocompact, properly discontinuous action by isometries. This conjecture was partially solved by Grigori Perelman in his proof[10][11][12] of the geometrization conjecture, which states (in part) than any Gromov hyperbolic group that is a 3-manifold group must act geometrically on hyperbolic 3-space. However, it still remains to show that a Gromov hyperbolic group with a 2-sphere at infinity is a 3-manifold group.
Cannon and Swenson showed [13] that a hyperbolic group with a 2-sphere at infinity has an associated subdivision rule. If this subdivision rule is conformal in a certain sense, the group will be a 3-manifold group with the geometry of hyperbolic 3-space.[7]
Combinatorial Riemann mapping theorem[edit]
Subdivision rules give a sequence of tilings of a surface, and tilings give an idea of distance, length, and area (by letting each tile have length and area 1). In the limit, the distances that come from these tilings may converge in some sense to an analytic structure on the surface. The Combinatorial Riemann Mapping Theorem gives necessary and sufficient conditions for this to occur.[7]
Its statement needs some background. A tiling of a ring (i.e., a closed annulus) gives two invariants, and , called approximate moduli. These are similar to the classical modulus of a ring. They are defined by the use of weight functions. A weight function assigns a non-negative number called a weight to each tile of . Every path in can be given a length, defined to be the sum of the weights of all tiles in the path. Define the height of under to be the infimum of the length of all possible paths connecting the inner boundary of to the outer boundary. The circumference of under is the infimum of the length of all possible paths circling the ring (i.e. not nullhomotopic in R). The area of under is defined to be the sum of the squares of all weights in . Then define
Note that they are invariant under scaling of the metric.
A sequence of tilings is conformal () if mesh approaches 0 and:
- For each ring , the approximate moduli and , for all sufficiently large, lie in a single interval of the form ; and
- Given a point in the surface, a neighborhood of , and an integer , there is a ring in separating x from the complement of , such that for all large the approximate moduli of are all greater than .[7]
Statement of theorem[edit]
If a sequence of tilings of a surface is conformal () in the above sense, then there is a conformal structure on the surface and a constant depending only on in which the classical moduli and approximate moduli (from for sufficiently large) of any given annulus are -comparable, meaning that they lie in a single interval .[7]
Consequences[edit]
The Combinatorial Riemann Mapping Theorem implies that a group acts geometrically on if and only if it is Gromov hyperbolic, it has a sphere at infinity, and the natural subdivision rule on the sphere gives rise to a sequence of tilings that is conformal in the sense above. Thus, Cannon's conjecture would be true if all such subdivision rules were conformal.[13]
References[edit]
- ^ a b c J. W. Cannon, W. J. Floyd, W. R. Parry. Finite subdivision rules. Conformal Geometry and Dynamics, vol. 5 (2001), pp. 153–196.
- ^ J. W. Cannon, W. J. Floyd, W. R. Parry. Constructing subdivision rules from rational maps. Conformal Geometry and Dynamics, vol. 11 (2007), pp. 128–136.
- ^ J. W. Cannon, W. J. Floyd, W. R. Parry. Lattès maps and subdivision rules. Conformal Geometry and Dynamics, vol. 14 (2010, pp. 113–140.
- ^ B. Rushton. Constructing subdivision rules from alternating links. Conform. Geom. Dyn. 14 (2010), 1–13.
- ^ Rushton, B. (2012). "A finite subdivision rule for the n-dimensional torus". Geometriae Dedicata. 167: 23–34. arXiv:1110.3310. doi:10.1007/s10711-012-9802-5. S2CID 119145306.
- ^ a b c d e f J. W. Cannon, W. Floyd and W. Parry. Crystal growth, biological cell growth and geometry. Pattern Formation in Biology, Vision and Dynamics, pp. 65–82. World Scientific, 2000. ISBN 981-02-3792-8, ISBN 978-981-02-3792-9.
- ^ a b c d e f g James W. Cannon. The combinatorial Riemann mapping theorem. Acta Mathematica 173 (1994), no. 2, pp. 155–234.
- ^ a b Lu, Peter J.; Steinhardt, Paul J. (2007). "Decagonal and Quasi-crystalline Tilings in Medieval Islamic Architecture" (PDF). Science. 315 (5815): 1106–1110. Bibcode:2007Sci...315.1106L. doi:10.1126/science.1135491. PMID 17322056. S2CID 10374218. Archived from the original (PDF) on 2009-10-07.
"Supporting Online Material" (PDF). Archived from the original (PDF) on 2009-03-26. - ^ D. Zorin. Subdivisions on arbitrary meshes: algorithms and theory. Institute of Mathematical Sciences (Singapore) Lecture Notes Series. 2006.
- ^ Perelman, Grisha (11 November 2002). "The entropy formula for the Ricci flow and its geometric applications". arXiv:math.DG/0211159.
- ^ Perelman, Grisha (10 March 2003). "Ricci flow with surgery on three-manifolds". arXiv:math.DG/0303109.
- ^ Perelman, Grisha (17 July 2003). "Finite extinction time for the solutions to the Ricci flow on certain three-manifolds". arXiv:math.DG/0307245.
- ^ a b J. W. Cannon and E. L. Swenson, Recognizing constant curvature discrete groups in dimension 3. Transactions of the American Mathematical Society 350 (1998), no. 2, pp. 809–849.
External links[edit]
- Bill Floyd's research page. This page contains most of the research papers by Cannon, Floyd and Parry on subdivision rules, as well as a gallery of subdivision rules.



































![{\displaystyle [r,Kr]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b649833f1c3e1e6d6a8ba88af4137c177f629217)






![{\displaystyle [r,K'r]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/884c02f2b1296a7d40f7b74147459ec5d2889464)

