Inscribed angle

In geometry, an inscribed angle is the angle formed in the interior of a circle when two chords intersect on the circle. It can also be defined as the angle subtended at a point on the circle by two given points on the circle.
Equivalently, an inscribed angle is defined by two chords of the circle sharing an endpoint.
The inscribed angle theorem relates the measure of an inscribed angle to that of the central angle subtending the same arc.
The inscribed angle theorem appears as Proposition 20 on Book 3 of Euclid's Elements.
Theorem[edit]
Statement[edit]
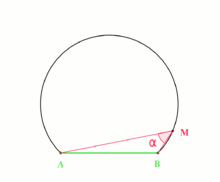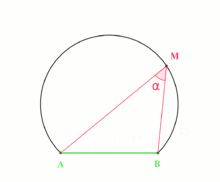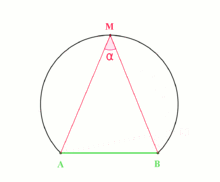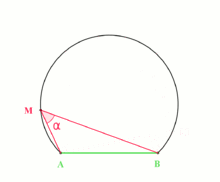
The inscribed angle theorem states that an angle θ inscribed in a circle is half of the central angle 2θ that subtends the same arc on the circle. Therefore, the angle does not change as its vertex is moved to different positions on the circle.
Proof[edit]
Inscribed angles where one chord is a diameter[edit]

Let O be the center of a circle, as in the diagram at right. Choose two points on the circle, and call them V and A. Draw line OV and extended past O so that it intersects the circle at point B which is diametrically opposite the point V. Draw an angle whose vertex is point V and whose sides pass through points A, B.
Draw line OA. Angle ∠BOA is a central angle; call it θ. Lines OV and OA are both radii of the circle, so they have equal lengths. Therefore, triangle △VOA is isosceles, so angle ∠BVA (the inscribed angle) and angle ∠VAO are equal; let each of them be denoted as ψ.
Angles ∠BOA and ∠AOV are supplementary, summing to a straight angle (180°), so angle ∠AOV measures 180° − θ.
The three angles of triangle △VOA must sum to 180°:
Adding to both sides yields
Inscribed angles with the center of the circle in their interior[edit]

Given a circle whose center is point O, choose three points V, C, D on the circle. Draw lines VC and VD: angle ∠DVC is an inscribed angle. Now draw line OV and extend it past point O so that it intersects the circle at point E. Angle ∠DVC subtends arc DC on the circle.
Suppose this arc includes point E within it. Point E is diametrically opposite to point V. Angles ∠DVE, ∠EVC are also inscribed angles, but both of these angles have one side which passes through the center of the circle, therefore the theorem from the above Part 1 can be applied to them.
Therefore,
then let
so that
Draw lines OC and OD. Angle ∠DOC is a central angle, but so are angles ∠DOE and ∠EOC, and
Let
so that
From Part One we know that and that . Combining these results with equation (2) yields
therefore, by equation (1),
Inscribed angles with the center of the circle in their exterior[edit]

The previous case can be extended to cover the case where the measure of the inscribed angle is the difference between two inscribed angles as discussed in the first part of this proof.
Given a circle whose center is point O, choose three points V, C, D on the circle. Draw lines VC and VD: angle ∠DVC is an inscribed angle. Now draw line OV and extend it past point O so that it intersects the circle at point E. Angle ∠DVC subtends arc DC on the circle.
Suppose this arc does not include point E within it. Point E is diametrically opposite to point V. Angles ∠EVD, ∠EVC are also inscribed angles, but both of these angles have one side which passes through the center of the circle, therefore the theorem from the above Part 1 can be applied to them.
Therefore,
then let
so that
Draw lines OC and OD. Angle ∠DOC is a central angle, but so are angles ∠EOD and ∠EOC, and
Let
so that
From Part One we know that and that . Combining these results with equation (4) yields

Corollary[edit]
By a similar argument, the angle between a chord and the tangent line at one of its intersection points equals half of the central angle subtended by the chord. See also Tangent lines to circles.
Applications[edit]

2𝜃 + 2𝜙 = 360° ∴ 𝜃 + 𝜙 = 180°
The inscribed angle theorem is used in many proofs of elementary Euclidean geometry of the plane. A special case of the theorem is Thales' theorem, which states that the angle subtended by a diameter is always 90°, i.e., a right angle. As a consequence of the theorem, opposite angles of cyclic quadrilaterals sum to 180°; conversely, any quadrilateral for which this is true can be inscribed in a circle. As another example, the inscribed angle theorem is the basis for several theorems related to the power of a point with respect to a circle. Further, it allows one to prove that when two chords intersect in a circle, the products of the lengths of their pieces are equal.
Inscribed angle theorems for ellipses, hyperbolas and parabolas[edit]
Inscribed angle theorems exist for ellipses, hyperbolas and parabolas, too. The essential differences are the measurements of an angle. (An angle is considered a pair of intersecting lines.)
References[edit]
- Ogilvy, C. S. (1990). Excursions in Geometry. Dover. pp. 17–23. ISBN 0-486-26530-7.
- Gellert W, Küstner H, Hellwich M, Kästner H (1977). The VNR Concise Encyclopedia of Mathematics. New York: Van Nostrand Reinhold. p. 172. ISBN 0-442-22646-2.
- Moise, Edwin E. (1974). Elementary Geometry from an Advanced Standpoint (2nd ed.). Reading: Addison-Wesley. pp. 192–197. ISBN 0-201-04793-4.
External links[edit]
- Weisstein, Eric W. "Inscribed Angle". MathWorld.
- Relationship Between Central Angle and Inscribed Angle
- Munching on Inscribed Angles at cut-the-knot
- Arc Central Angle With interactive animation
- Arc Peripheral (inscribed) Angle With interactive animation
- Arc Central Angle Theorem With interactive animation
- At bookofproofs.github.io




















