Majority judgment
| Part of the Politics series |
| Electoral systems |
|---|
 |
|
|
Majority judgment (MJ) is a single-winner voting system proposed in 2010 by Michel Balinski and Rida Laraki.[1][2][3] It is a kind of highest median rule, a cardinal voting system that elects the candidate with the highest median rating.
Voting process[edit]
Voters grade as many of the candidates as they wish with regard to their suitability for office according to a series of grades. Balinski and Laraki suggest the options "Excellent, Very Good, Good, Acceptable, Poor, or Reject," but any scale can be used (e.g. the common letter grade scale). Voters can assign the same grade to multiple candidates.
As with all highest median voting rules, the candidate with the highest median grade is declared winner. If more than one candidate has the same median grade, majority judgment breaks the tie by removing (one-by-one) any grades equal to the shared median grade from each tied candidate's column. This procedure is repeated until only one of the tied candidates is found to have the highest median grade.[4]
Advantages and disadvantages[edit]
Like most other cardinal voting rules, majority judgment satisfies the monotonicity criterion, the later-no-help criterion, and independence of irrelevant alternatives.
Like any deterministic voting system (except dictatorship), MJ allows for tactical voting in cases of more than three candidates, as a consequence of Gibbard's theorem.
Majority judgment voting fails the Condorcet criterion,[a] later-no-harm,[b]consistency,[c] the Condorcet loser criterion, the participation criterion, the majority criterion,[d] and the mutual majority criterion.
Participation failure[edit]
Unlike score voting, majority judgment can have no-show paradoxes,[5] situations where a candidate loses because they won "too many votes". In other words, adding votes that rank a candidate higher than their opponent can still cause this candidate to lose.
In their 2010 book, Balinski and Laraki demonstrate that the only join-consistent methods are point-summing methods, a slight generalization of score voting that includes positional voting.[6] Specifically, their result shows the only methods satisfying the slightly stronger consistency criterion have:
Where is a monotonic function. Moreover, any method satisfying both participation and either stepwise-continuity or the Archimedean property[e] is a point-summing method.[7]
This result is closely related to and relies on the Von Neumann–Morgenstern utility theorem and Harsanyi's utilitarian theorem, two critical results in social choice theory and decision theory used to characterize the conditions for rational choice.
Despite this result, Balinski and Laraki claim that participation failures would be rare in practice for majority judgment.[6]
Claimed resistance to tactical voting[edit]
In arguing for majority judgment, Balinski and Laraki (the system's inventors) prove highest median rules are the most "strategy-resistant" system, in the sense that they minimize the share of the electorate with an incentive to be dishonest.[8] However, some writers have disputed the significance of these results, as they do not apply in cases of imperfect information or collusion between voters.[citation needed]
Median voter property[edit]
In "left-right" environments, majority judgment tends to favor the most homogeneous camp, instead of picking the middle-of-the-road, Condorcet winner candidate.[9] Majority judgment therefore fails the median voter criterion.[10]
Here is a numerical example. Suppose there were seven ratings named "Excellent," "Very good," "Good", "Mediocre," "Bad," "Very Bad," and "Awful." Suppose voters belong to seven groups ranging from "Far-left" to "Far-right," and each group runs a single candidate. Voters assign candidates from their own group a rating of "Excellent," then decrease the rating as candidates are politically further away from them.
Votes Candidate |
101 votes
Far-left |
101 votes
Left |
101 votes
Cen. left |
50 votes
Center |
99 votes
Cen. right |
99 votes
Right |
99 votes
Far-right |
Score |
|---|---|---|---|---|---|---|---|---|
| Far left | excel. | v. good | good | med. | bad | very bad | awful | med. |
| Left | v. good | excel. | v. good | good | med. | bad | very bad | good |
| Cen. left | good | v. good | excel. | v. good | good | med. | bad | good |
| Center | med. | good | v. good | excel. | v. good | good | med. | good |
| Cen. right | bad | med. | good | v. good | excel. | v. good | good | good |
| Right | very bad | bad | med. | good | v. good | excel. | v. good | good |
| Far right | awful | very bad | bad | med. | good | v. good | excel. | med. |
The tie-breaking procedure of majority judgment elects the Left candidate, as this candidate is the one with the non-median rating closest to the median, and this non-median rating is above the median rating. In so doing, the majority judgment elects the best compromise for voters on the left side of the political axis (as they are slightly more numerous than those on the right) instead of choosing a more consensual candidate such as the center-left or the center. The reason is that the tie-breaking is based on the rating closest to the median, regardless of the other ratings.
Note that other highest median rules such as graduated majority judgment will often make different tie-breaking decisions (and graduated majority judgment would elect the Center candidate). These methods, introduced more recently, maintain many desirable properties of majority judgment while avoiding the pitfalls of its tie-breaking procedure.[11]
| Candidate |
| |||||||||||||
| Left |
| |||||||||||||
| Center left |
| |||||||||||||
| Center |
| |||||||||||||
| Center right |
| |||||||||||||
| Right |
| |||||||||||||
|
Example application[edit]
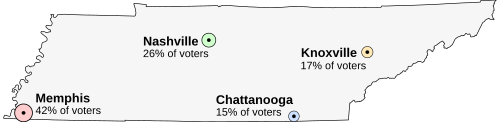
Suppose that Tennessee is holding an election on the location of its capital. The population is concentrated around four major cities. All voters want the capital to be as close to them as possible. The options are:
- Memphis, the largest city, but far from the others (42% of voters)
- Nashville, near the center of the state (26% of voters)
- Chattanooga, somewhat east (15% of voters)
- Knoxville, far to the northeast (17% of voters)
The preferences of each region's voters are:
| 42% of voters Far-West |
26% of voters Center |
15% of voters Center-East |
17% of voters Far-East |
|---|---|---|---|
|
|
|
|
Suppose there were four ratings named "Excellent", "Good", "Fair", and "Poor", and voters assigned their ratings to the four cities by giving their own city the rating "Excellent", the farthest city the rating "Poor" and the other cities "Good", "Fair", or "Poor" depending on whether they are less than a hundred, less than two hundred, or over two hundred miles away:
City Choice |
Memphis voters |
Nashville voters |
Chattanooga voters |
Knoxville voters |
Median rating[f] |
|---|---|---|---|---|---|
| Memphis | excellent | poor | poor | poor | poor+ |
| Nashville | fair | excellent | fair | fair | fair+ |
| Chattanooga | poor | fair | excellent | good | fair- |
| Knoxville | poor | fair | good | excellent | fair- |
Then the sorted scores would be as follows:
| City |
| |||||||||
| Nashville |
| |||||||||
| Knoxville |
| |||||||||
| Chattanooga |
| |||||||||
| Memphis |
| |||||||||
|
The median ratings for Nashville, Chattanooga, and Knoxville are all "Fair"; and for Memphis, "Poor". Since there is a tie between Nashville, Chattanooga, and Knoxville, "Fair" ratings are removed from all three, until their medians become different. After removing 16% "Fair" ratings from the votes of each, the sorted ratings are now:
| City |
| ||||||
| Nashville |
| ||||||
| Knoxville |
| ||||||
| Chattanooga |
|
Chattanooga and Knoxville now have the same number of "Poor" ratings as "Fair", "Good" and "Excellent" combined. As a result of subtracting one "Fair" from each of the tied cities, one-by-one until only one of these cities has the highest median-grade, the new and deciding median-grades of these originally tied cities are as follows: "Poor" for both Chattanooga and Knoxville, while Nashville's median remains at "Fair". So Nashville, the capital in real life, wins.
Real-world examples[edit]
The somewhat-related median voting rule method was first explicitly proposed to assign budgets by Francis Galton in 1907.[12] Hybrid mean/median systems based on the trimmed mean have long been used to assign scores in contests such as Olympic figure skating, where they are intended to limit the impact of biased or strategic judges.
The first highest median rule to be developed was Bucklin voting, a system used by Progressive era reformers in the United States.
The full system of majority judgment was first proposed by Balinski and Laraki in 2007.[1] That same year, they used it in an exit poll of French voters in the presidential election. Although this regional poll was not intended to be representative of the national result, it agreed with other local or national experiments in showing that François Bayrou, rather than the eventual runoff winner, Nicolas Sarkozy, or two other candidates (Ségolène Royal or Jean-Marie Le Pen) would have won under most alternative rules, including majority judgment. They also note:
Everyone with some knowledge of French politics who was shown the results with the names of Sarkozy, Royal, Bayrou and Le Pen hidden invariably identified them: the grades contain meaningful information.[13]
It has since been used in judging wine competitions and in other political research polling in France and in the US.[14]
Variants[edit]
Varloot and Laraki[15] present a variant of majority judgement, called majority judgement with uncertainty (MJU), which allows voters to express uncertainty about each candidate's merits.
See also[edit]
- Usual judgment
- Approval voting
- Range voting
- Voting system
- List of democracy and elections-related topics
Notes[edit]
- ^ Strategically in the strong Nash equilibrium, MJ passes the Condorcet criterion, just like score voting.
- ^ MJ provides a weaker guarantee similar to LNH: rating another candidate at or below your preferred winner's median rating (as opposed to one's own rating for the winner) cannot harm the winner.
- ^ Majority judgment's inventors argue that meaning should be assigned to the absolute rating that the system assigns to a candidate; that if one electorate rates candidate X as "excellent" and Y as "good", while another one ranks X as "acceptable" and Y as "poor", these two electorates do not in fact agree. Therefore, they define a criterion they call "rating consistency", which majority judgment passes. Balinski and Laraki, "Judge, don't Vote", November 2010
- ^ MJ satisfies a weakened version of the majority criterion—if only one candidate receives perfect grades from a majority of all voters, this candidate will win.
- ^ Balinski and Laraki refer to this property as "respect for large electorates."
- ^ A "+" or "-" is added depending on whether the median would rise or fall if median ratings were removed, as in the tie-breaking procedure.
References[edit]
- ^ a b Balinski M. and R. Laraki (2007) «A theory of measuring, electing and ranking». Proceedings of the National Academy of Sciences USA, vol. 104, no. 21, 8720-8725.
- ^ Balinski, M.; Laraki, R. (2010). Majority Judgment. MIT. ISBN 978-0-262-01513-4.
- ^ de Swart, Harrie (2021-11-16). "How to Choose a President, Mayor, Chair: Balinski and Laraki Unpacked". The Mathematical Intelligencer. 44 (2): 99–107. doi:10.1007/s00283-021-10124-3. ISSN 0343-6993. S2CID 244289281.
- ^ Balinski and Laraki, Majority Judgment, pp.5 & 14
- ^ Felsenthal, Dan S. and Machover, Moshé, "The Majority Judgement voting procedure: a critical evaluation", Homo oeconomicus, vol 25(3/4), pp. 319-334 (2008)
- ^ a b Balinski, Michel; Laraki, Rida (2011-01-28), "Majority Judgment", The MIT Press, pp. 295–301, doi:10.7551/mitpress/9780262015134.003.0001, ISBN 978-0-262-01513-4, retrieved 2024-02-08
{{citation}}: Missing or empty|title=(help) - ^ Balinski, Michel; Laraki, Rida (2011-01-28), "Majority Judgment", The MIT Press, pp. 300–301, doi:10.7551/mitpress/9780262015134.003.0001, ISBN 978-0-262-01513-4, retrieved 2024-02-08
{{citation}}: Missing or empty|title=(help) - ^ Balinski and Laraki, Majority Judgment, pp. 15,17,19,187-198, and 374
- ^ Jean-François Laslier (2010). "On choosing the alternative with the best median evaluation". Public Choice.
- ^ Jean-François Laslier (2018). "The strange "Majority Judgment"". Hal.
- ^ Fabre, Adrien (2020). "Tie-breaking the Highest Median: Alternatives to the Majority Judgment" (PDF). Social Choice and Welfare. 56: 101–124. doi:10.1007/s00355-020-01269-9. S2CID 253851085.
- ^ Francis Galton, "One vote, one value," Letter to the editor, Nature vol. 75, Feb. 28, 1907, p. 414.
- ^ Balinski M. and R. Laraki (2007) «Election by Majority Judgment: Experimental Evidence». Cahier du Laboratoire d’Econométrie de l’Ecole Polytechnique 2007-28. Chapter in the book: «In Situ and Laboratory Experiments on Electoral Law Reform: French Presidential Elections», Edited by Bernard Dolez, Bernard Grofman and Annie Laurent. Springer, to appear in 2011.
- ^ Balinski M. and R. Laraki (2010) «Judge: Don't vote». Cahier du Laboratoire d’Econométrie de l’Ecole Polytechnique 2010-27.
- ^ Varloot, Estelle Marine; Laraki, Rida (2022-07-13). "Level-strategyproof Belief Aggregation Mechanisms". Proceedings of the 23rd ACM Conference on Economics and Computation. EC '22. New York, NY, USA: Association for Computing Machinery. pp. 335–369. arXiv:2108.04705. doi:10.1145/3490486.3538309. ISBN 978-1-4503-9150-4.
Further reading[edit]
- Balinski, Michel, and Laraki, Rida (2010). Majority Judgment: Measuring, Ranking, and Electing, MIT Press