Triangular bipyramid
| Triangular bipyramid | |
|---|---|
 | |
| Type | Bipyramid Deltahedra Johnson J11 – J12 – J13 |
| Faces | 6 triangles |
| Edges | 9 |
| Vertices | 5 |
| Vertex configuration | |
| Symmetry group | |
| Dual polyhedron | triangular prism |
| Properties | convex |
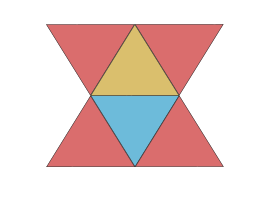
| Net | |
 | |
In geometry, the triangular bipyramid is the hexahedron with six triangular faces, constructed by attaching two tetrahedrons face-to-face. The same shape is also called the triangular dipyramid[1][2] or trigonal bipyramid.[3] If these tetrahedrons are regular, all faces of triangular bipyramid are equilateral. It is an example of a deltahedron and of a Johnson solid.
Many polyhedrons are related to the triangular bipyramid, such as new similar shapes derived in different approaches, and the triangular prism as its dual polyhedron. The many applications of triangular bipyramid include the trigonal bipyramid molecular geometry that describes its atom cluster, the solution of Thomson problem, and the representation of color order systems by the eighteenth century. The triangular bipyramid has a graph with its construction involving the wheel graph.
Construction[edit]
Like other bipyramids, the triangular bipyramid can be constructed by attaching two tetrahedrons face-to-face.[2] These tetrahedrons cover their triangular base, such that the resulting polyhedron has six triangles, five vertices, and nine edges.[3] The triangular bipyramid is said to be right if the tetrahedrons are symmetrically regular and both of their apices are on the line passing through the center of base; otherwise, it is oblique.[4][5] If the tetrahedrons are regular, then all edges of the triangular bipyramid are equal in length, making up the faces are equilateral triangles. A polyhedron with only equilateral triangles as faces is called a deltahedron. There are only eight different convex deltahedra, one of which is the triangular bipyramid with regular faces.[1] More generally, the convex polyhedron in which all of the faces are regular is the Johnson solid, and every convex deltahedron is a Johnson solid. The triangular bipyramid with the regular faces is among numbered the Johnson solids as , the twelfth Johnson solid.[6]
Properties[edit]
A triangular bipyramid's surface area is six times that of all triangles. In the case of edge length , its surface area is:[7]
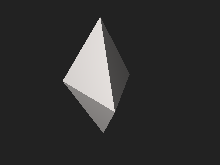
The triangular bipyramid has three-dimensional point group symmetry, the dihedral group of order twelve: the appearance of the triangular bipyramid is unchanged as it rotated by one-, two-thirds, and full angle around the axis of symmetry (a line passing through two vertices and base's center vertically), and it has mirror symmetry relative to any bisector of the base; it is also symmetrical by reflecting it across a horizontal plane. The dihedral angle of a triangular bipyramid with regular faces can be calculated by adding the angle of two regular tetrahedra: the angle of tetrahedron between adjacent triangular faces itself is , and the dihedral angle of adjacent triangles, on the edge where two tetrahedra attaching is twice that:[8]
Graph[edit]

According to Steinitz's theorem, a graph can be represented as the skeleton of a polyhedron if it is planar and 3-connected graph. In other words, the edges of that graph do not cross but only intersect at the point, and one of any two vertices leaves a connected subgraph when removed. The triangular bipyramid is represented by a graph with nine edges, constructed by adding one vertex connecting to three other vertices of wheel graph , where represents the graph of pyramid with -sided polygonal base.[9][10]
Sajjad, Sardar & Pan (2024) constructed a chain of triangular bipyramid graphs by arranging them linearly, as in the illustration below. The resistance distance (measurement of two vertices of a graph using the electrical network) of such construction can be computed by applying the series and parallel principles, star-mesh transformation, and Y-Δ transformation. Its structure is an example of the metal-organic frameworks study.[11]
Related polyhedra[edit]

Some types of triangular bipyramids may be derived in different ways. For example, the Kleetope of polyhedra is a construction involving the attachment of pyramids; in the case of the triangular bipyramid, its Kleetope can be constructed from triangular bipyramid by attaching tetrahedrons onto each of its faces, covering and replacing them with other three triangles; the skeleton of resulting polyhedron represents the Goldner–Harary graph.[12][13] Another type of triangular bipyramid is by cutting off all of its vertices; this process is known as truncation.[14]
The bipyramids are the dual polyhedron of prisms, for which the bipyramids' vertices correspond to the faces of the prism, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Consequently, the dualization of a dual polyhedron is the original polyhedron itself. Hence, the triangular bipyramid is the dual polyhedron of the triangular prism, and vice versa.[15][3] The triangular prism has five faces, nine edges, and six vertices, and it has the same symmetry as the triangular bipyramid.[3]
Applications[edit]

The Thomson problem concerns the minimum-energy configuration of charged particles on a sphere. One of them is a triangular bipyramid, which is a known solution for the case of five electrons, by placing vertices of a triangular bipyramid inscribed in a sphere.[16] This solution is aided by the mathematically rigorous computer.[17]
In the geometry of chemical compound, the trigonal bipyramidal molecular geometry may be described as the atom cluster of the triangular bipyramid. This molecule has a main-group element without an active lone pair, as described by a model that predicts the geometry of molecules known as VSEPR theory.[18] Some examples of this structure are the phosphorus pentafluoride and phosphorus pentachloride in the gas phase.[19]
In the study of color theory, the triangular bipyramid was used to represent the three-dimensional color order system in primary color. The German astronomer Tobias Mayer presented in 1758 that each of its vertices represents the colors: white and black are, respectively, the top and bottom vertices, whereas the rest of the vertices are red, blue, and yellow.[20][21]
References[edit]
- ^ a b Trigg, Charles W. (1978). "An infinite class of deltahedra". Mathematics Magazine. 51 (1): 55–57. doi:10.1080/0025570X.1978.11976675. JSTOR 2689647. MR 1572246.
- ^ a b Rajwade, A. R. (2001). Convex Polyhedra with Regularity Conditions and Hilbert's Third Problem. Texts and Readings in Mathematics. Hindustan Book Agency. p. 84. doi:10.1007/978-93-86279-06-4. ISBN 978-93-86279-06-4.
- ^ a b c d King, Robert B. (1994). "Polyhedral Dynamics". In Bonchev, Danail D.; Mekenyan, O.G. (eds.). Graph Theoretical Approaches to Chemical Reactivity. Springer. doi:10.1007/978-94-011-1202-4. ISBN 978-94-011-1202-4.
- ^ Niu, Wenxin; Xu, Guobao (2011). "Crystallographic control of noble metal nanocrystals". Nano Today. 6 (3): 265–285. doi:10.1016/j.nantod.2011.04.006.
- ^ Alexandrov, Victor (2017). "How many times can the volume of a convex polyhedron be increased by isometric deformations?". Beiträge zur Algebra und Geometrie. 58 (3): 549–554. arXiv:1607.06604. doi:10.1007/s13366-017-0336-8.
- ^ Uehara, Ryuhei (2020). Introduction to Computational Origami: The World of New Computational Geometry. Springer. doi:10.1007/978-981-15-4470-5. ISBN 978-981-15-4470-5. S2CID 220150682.
- ^ a b Berman, Martin (1971). "Regular-faced convex polyhedra". Journal of the Franklin Institute. 291 (5): 329–352. doi:10.1016/0016-0032(71)90071-8. MR 0290245.
- ^ Johnson, Norman W. (1966). "Convex polyhedra with regular faces". Canadian Journal of Mathematics. 18: 169–200. doi:10.4153/cjm-1966-021-8. MR 0185507. S2CID 122006114. Zbl 0132.14603.
- ^ Tutte, W. T. (2001). Graph Theory. Cambridge University Press. p. 113. ISBN 978-0-521-79489-3.
- ^ Pisanski, Tomaž; Servatius, Brigitte (2013). Configuration from a Graphical Viewpoint. Springer. p. 21. doi:10.1007/978-0-8176-8364-1. ISBN 978-0-8176-8363-4.
- ^ Sajjad, Wassid; Sardar, Muhammad S.; Pan, Xiang-Feng (2024). "Computation of resistance distance and Kirchhoff index of chain of triangular bipyramid hexahedron". Applied Mathematics and Computation. 461: 1–12. doi:10.1016/j.amc.2023.128313. S2CID 261797042.
- ^ Grünbaum, Branko (1967). Convex Polytopes. Wiley Interscience. p. 357.. Same page, 2nd ed., Graduate Texts in Mathematics 221, Springer-Verlag, 2003, ISBN 978-0-387-40409-7.
- ^ Ewald, Günter (1973). "Hamiltonian circuits in simplicial complexes". Geometriae Dedicata. 2 (1): 115–125. doi:10.1007/BF00149287. S2CID 122755203.
- ^ Haji-Akbari, Amir; Chen, Elizabeth R.; Engel, Michael; Glotzer, Sharon C. (2013). "Packing and self-assembly of truncated triangular bipyramids". Phys. Rev. E. 88 (1): 012127. arXiv:1304.3147. Bibcode:2013PhRvE..88a2127H. doi:10.1103/physreve.88.012127. PMID 23944434. S2CID 8184675..
- ^ Sibley, Thomas Q. (2015). Thinking Geometrically: A Survey of Geometries. Mathematical Association of American. p. 53. ISBN 978-1-939512-08-6.
- ^ Sloane, N. J. A.; Hardin, R. H.; Duff, T. D. S.; Conway, J. H. (1995), "Minimal-energy clusters of hard spheres", Discrete & Computational Geometry, 14 (3): 237–259, doi:10.1007/BF02570704, MR 1344734, S2CID 26955765
- ^ Schwartz, Richard Evan (2013). "The Five-Electron Case of Thomson's Problem". Experimental Mathematics. 22 (2): 157–186. doi:10.1080/10586458.2013.766570. S2CID 38679186.
- ^ Petrucci, R. H.; W. S., Harwood; F. G., Herring (2002). General Chemistry: Principles and Modern Applications (8th ed.). Prentice-Hall. pp. 413–414. ISBN 978-0-13-014329-7. See table 11.1.
- ^ Housecroft, C. E.; Sharpe, A. G. (2004). Inorganic Chemistry (2nd ed.). Prentice Hall. p. 407. ISBN 978-0-13-039913-7.
- ^ Kuehni, Rolf G. (2003). Color Space and Its Divisions: Color Order from Antiquity to the Present. John & Sons Wiley. p. 53. ISBN 978-0-471-46146-3.
- ^ Kuehni, Rolf G. (2013). Color: An Introduction to Practice and Principles. John & Sons Wiley. p. 198. ISBN 978-1-118-17384-8.












